【同步作业】人教版九(上) 第22章 二次函数 专题四 几何图形中面积的最值问题——教材P57复习题22T9的变式及应用 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 第22章 二次函数 专题四 几何图形中面积的最值问题——教材P57复习题22T9的变式及应用 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览




文档简介
(共14张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
教材母题
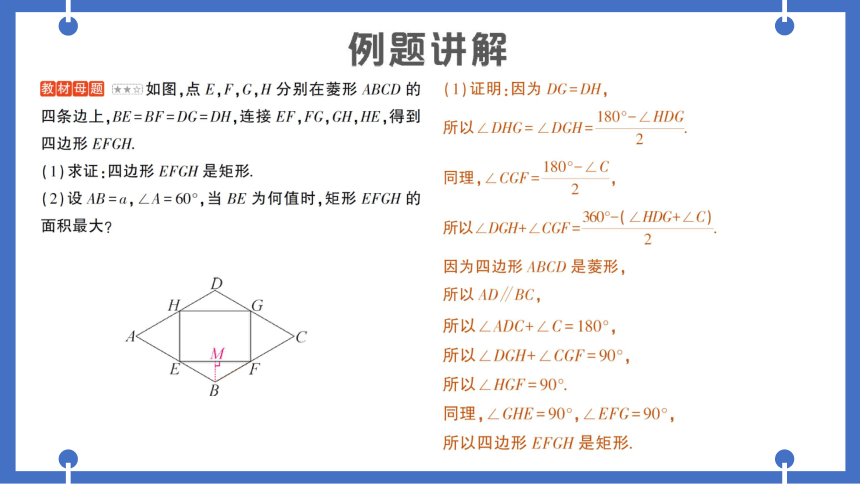
如图,点E,F,G,H分别在菱形ABCD的
四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到
四边形EFGH.
(1)求证:四边形EFGH是矩形
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的
面积最大?
D
H
G
A
C
M
E
B
(1)证明:因为DG=DH,
180°-∠HDG
所以∠DHG=∠DGH=
2
180°-∠C
同理,∠CGF=
2
360°-(∠HDG+∠C)
所以∠DGH+∠CGF=
2
因为四边形ABCD是菱形,
所以AD∥BC,
所以∠ADC+∠C=180°,
所以∠DGH+∠CGF=90°,
所以ㄥHGF=90°.
同理,∠GHE=90°,∠EFG=90°,
所以四边形EFGH是矩形.
设BE=x,则AE=a-x
因为BE=DH,所以AH=AE.
又∠A=60°,所以△AEH是等边三角形,
所以∠AEH=60°,EH=AE=a-x.
因为BM⊥EF,BE=BF,
所以∠BME=90°,EM=FM.
在Rt△BME中,∠BEM=180°-∠AEH-∠HEM=30°,BE
=x,所以BM=
所以S矩形ErGw=EF·EH=√3x(a-x)=-√3(x2-ax)=
3-2+
因为3<0,所以当x=)时,SE形最大,即当BE=时,
2
矩形EFGH的面积最大
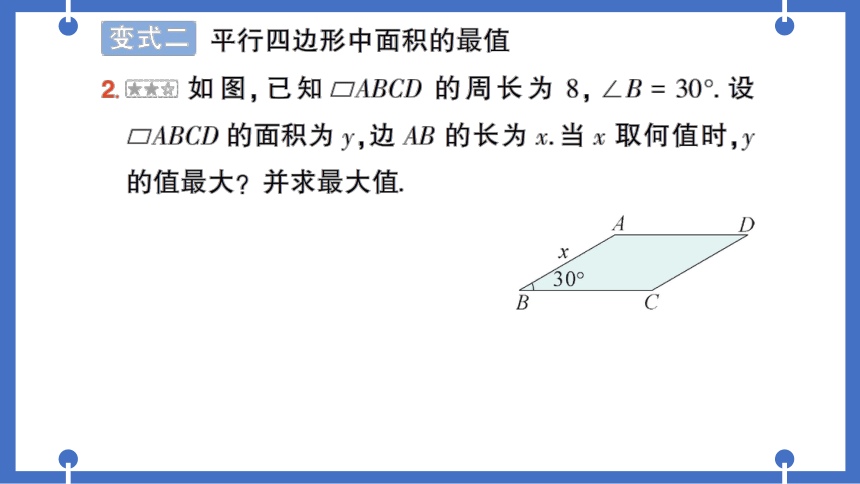
变式一
三角形中面积的最值
1.「教材P52习题22.3T6变式题7如图,已知△ABC,∠A
=30°,∠C=90°,BC=6.现准备在△ABC中剪出一个
□AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE
=X.
(1)求当x=2时,口AGEF的面积.
(2)当x为何值时,口AGEF的面积最大?最大面积是
多少?
解:设 AGEF的面积是S.
因为四边形AGEF是平行四边形,所以EF∥AG.
所以∠CFE=∠A=30°.
B
又∠C=90°,CE=x,BC=6,
所以EF=2CE=2x,AB=2BC=12,
所以CF=WEF2-CE=√(2x)2-x2=√/3x,AC=WAB2-BC2=√/122-62=
6W3,
所以AF=6√3-√3x.
所以S=AF·CE=(6W3-3x)x=-√/3x2+6W3x.
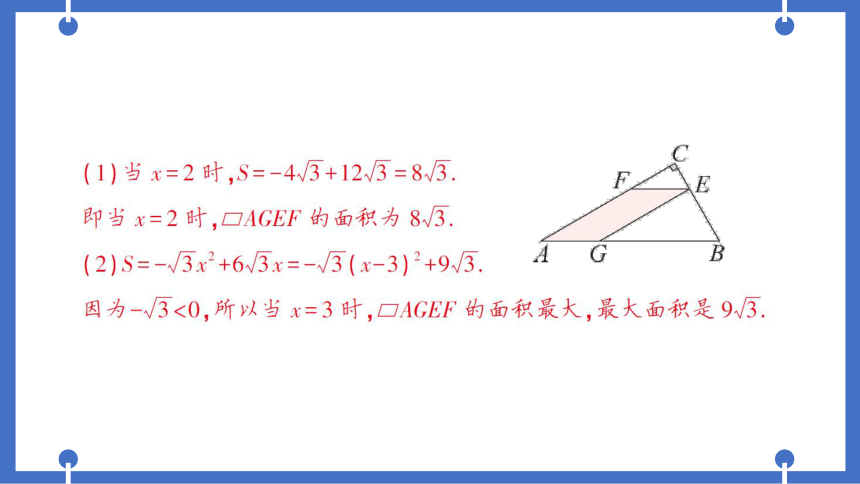
(1)当x=2时,S=-4W3+12√3=8√3.
即当x=2时,□AGEF的面积为8√3.
(2)S=-√3x2+6W3x=-√3(x-3)2+9W3.
因为-√3<0,所以当x=3时, AGEF的面积最大,最大面积是9√/3.
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
教材母题
如图,点E,F,G,H分别在菱形ABCD的
四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到
四边形EFGH.
(1)求证:四边形EFGH是矩形
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的
面积最大?
D
H
G
A
C
M
E
B
(1)证明:因为DG=DH,
180°-∠HDG
所以∠DHG=∠DGH=
2
180°-∠C
同理,∠CGF=
2
360°-(∠HDG+∠C)
所以∠DGH+∠CGF=
2
因为四边形ABCD是菱形,
所以AD∥BC,
所以∠ADC+∠C=180°,
所以∠DGH+∠CGF=90°,
所以ㄥHGF=90°.
同理,∠GHE=90°,∠EFG=90°,
所以四边形EFGH是矩形.
设BE=x,则AE=a-x
因为BE=DH,所以AH=AE.
又∠A=60°,所以△AEH是等边三角形,
所以∠AEH=60°,EH=AE=a-x.
因为BM⊥EF,BE=BF,
所以∠BME=90°,EM=FM.
在Rt△BME中,∠BEM=180°-∠AEH-∠HEM=30°,BE
=x,所以BM=
所以S矩形ErGw=EF·EH=√3x(a-x)=-√3(x2-ax)=
3-2+
因为3<0,所以当x=)时,SE形最大,即当BE=时,
2
矩形EFGH的面积最大
变式一
三角形中面积的最值
1.「教材P52习题22.3T6变式题7如图,已知△ABC,∠A
=30°,∠C=90°,BC=6.现准备在△ABC中剪出一个
□AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE
=X.
(1)求当x=2时,口AGEF的面积.
(2)当x为何值时,口AGEF的面积最大?最大面积是
多少?
解:设 AGEF的面积是S.
因为四边形AGEF是平行四边形,所以EF∥AG.
所以∠CFE=∠A=30°.
B
又∠C=90°,CE=x,BC=6,
所以EF=2CE=2x,AB=2BC=12,
所以CF=WEF2-CE=√(2x)2-x2=√/3x,AC=WAB2-BC2=√/122-62=
6W3,
所以AF=6√3-√3x.
所以S=AF·CE=(6W3-3x)x=-√/3x2+6W3x.
(1)当x=2时,S=-4W3+12√3=8√3.
即当x=2时,□AGEF的面积为8√3.
(2)S=-√3x2+6W3x=-√3(x-3)2+9W3.
因为-√3<0,所以当x=3时, AGEF的面积最大,最大面积是9√/3.
同课章节目录
