【同步作业】人教版九(上) 第22章 二次函数 专题十 二次函数与角度问题 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 第22章 二次函数 专题十 二次函数与角度问题 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:30 | ||
图片预览








文档简介
(共22张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1
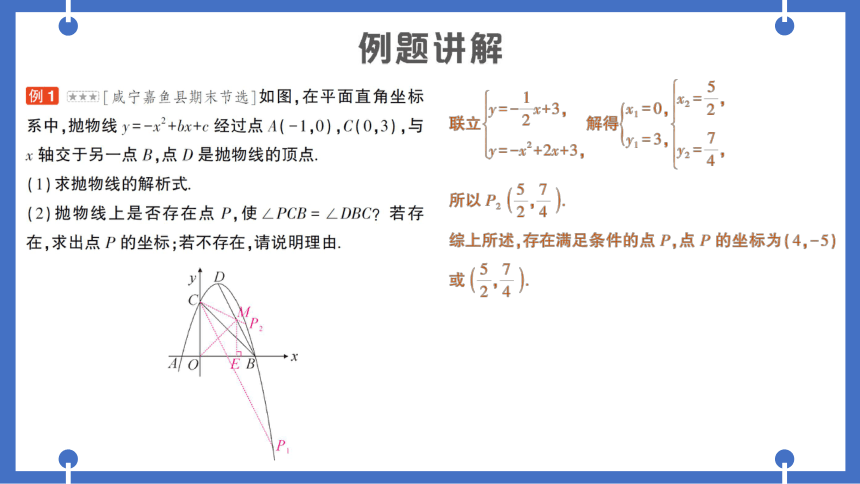
「咸宁嘉鱼县期末节选]如图,在平面直角坐标
系中,抛物线y=-x2+bx+c经过点A(-1,0),C(0,3),与
x轴交于另一点B,点D是抛物线的顶点,
(1)求抛物线的解析式
(2)抛物线上是否存在点P,使∠PCB=∠DBC 若存
在,求出点P的坐标;若不存在,请说明理由.
:
A,O
E
B
P
(2)存在.分两种情况讨论:
①若点P在第四象限,如图,∠P,CB
∠DBC,则CP∥DB.由(1)易求得B(3,
0),D(1,4),
所以直线DB的解析式为y=-2x+6.
因为CP,∥DB,
所以设直线CP,的解析式为y=-2x+d
将C(0,3)代入,得d=3,
所以直线CP,的解析式为y=-2x+3.
联立
y=-2x+3,
x1=0,x2=4,
解得
y=-x2+2x+3,
1=3,,=-5,
所以P(4,-5)
②若点P在第一象限,如图,∠P,CB=∠DBC,设CP,交DB
于点M,连接OM,则MC=MB.因为OB=OC,所以直线OM
垂直平分线段BC,所以易得∠MOB=45°.
过点M作ME⊥x轴于点E,则ME=OE.
设M(a,a).因为点M在直线DB:y=-2x+6上,以-2a+6=
a,解得a=2,所以M(2,2),易得直线CP,的解析式为y=
1
x+3.
2
5
二
。x+3,
x1=0,
2
联立
解得
y=3,
7
y=-x2+2x+3,
4
所以r,3,
综上所述,存在满足条件的点P,点P的坐标为(4,-5)
或(
5
y
C
A
B
O
y
C
B
O
y↑
A
B
H
文
C
P
B
X
P
2
②当点P在BC下方时,如图②,设PC交x轴于点H.因为∠PCB=
∠ABC,所以CH=BH.设BH=CH=m,则OH=OB-BH=8-m.在Rt△COH
中,0C2+0H=C,所以42+(8-m)2=m2,解得m=5,所以0H=3,所以
4
M3,01.使i线PC的阴格式为y-低+n,则得0
解得
3’所
n=4,
4
y=
3
以直线PC的解折式为y=-3x+4,联立
解得
3
x+4,
1=0,/._
34
100
y1=4,{x=3=
(6,4(,
1-2★「鄂尔多斯中考节选]如图,在平面直角坐标系中,
抛物线=a2+x+2经过1〔-2,0),B(3,2)两点,
与y轴交于点C.
(1)求抛物线的解析式
(2)抛物线上是否存在点Q,使∠QCB=45°?若存在,请
直接写出点O的坐标:若不存在,请说明理由.
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1
「咸宁嘉鱼县期末节选]如图,在平面直角坐标
系中,抛物线y=-x2+bx+c经过点A(-1,0),C(0,3),与
x轴交于另一点B,点D是抛物线的顶点,
(1)求抛物线的解析式
(2)抛物线上是否存在点P,使∠PCB=∠DBC 若存
在,求出点P的坐标;若不存在,请说明理由.
:
A,O
E
B
P
(2)存在.分两种情况讨论:
①若点P在第四象限,如图,∠P,CB
∠DBC,则CP∥DB.由(1)易求得B(3,
0),D(1,4),
所以直线DB的解析式为y=-2x+6.
因为CP,∥DB,
所以设直线CP,的解析式为y=-2x+d
将C(0,3)代入,得d=3,
所以直线CP,的解析式为y=-2x+3.
联立
y=-2x+3,
x1=0,x2=4,
解得
y=-x2+2x+3,
1=3,,=-5,
所以P(4,-5)
②若点P在第一象限,如图,∠P,CB=∠DBC,设CP,交DB
于点M,连接OM,则MC=MB.因为OB=OC,所以直线OM
垂直平分线段BC,所以易得∠MOB=45°.
过点M作ME⊥x轴于点E,则ME=OE.
设M(a,a).因为点M在直线DB:y=-2x+6上,以-2a+6=
a,解得a=2,所以M(2,2),易得直线CP,的解析式为y=
1
x+3.
2
5
二
。x+3,
x1=0,
2
联立
解得
y=3,
7
y=-x2+2x+3,
4
所以r,3,
综上所述,存在满足条件的点P,点P的坐标为(4,-5)
或(
5
y
C
A
B
O
y
C
B
O
y↑
A
B
H
文
C
P
B
X
P
2
②当点P在BC下方时,如图②,设PC交x轴于点H.因为∠PCB=
∠ABC,所以CH=BH.设BH=CH=m,则OH=OB-BH=8-m.在Rt△COH
中,0C2+0H=C,所以42+(8-m)2=m2,解得m=5,所以0H=3,所以
4
M3,01.使i线PC的阴格式为y-低+n,则得0
解得
3’所
n=4,
4
y=
3
以直线PC的解折式为y=-3x+4,联立
解得
3
x+4,
1=0,/._
34
100
y1=4,{x=3=
(6,4(,
1-2★「鄂尔多斯中考节选]如图,在平面直角坐标系中,
抛物线=a2+x+2经过1〔-2,0),B(3,2)两点,
与y轴交于点C.
(1)求抛物线的解析式
(2)抛物线上是否存在点Q,使∠QCB=45°?若存在,请
直接写出点O的坐标:若不存在,请说明理由.
同课章节目录
