【同步作业】人教版九(上) 第23章 旋转 专题十二 旋转中的常见模型 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 第23章 旋转 专题十二 旋转中的常见模型 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:30 | ||
图片预览




文档简介
(共17张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1
★☆如图①,在等腰直角三角形ABC中,∠ACB
90°,E是边AC上任意一点(点E与点A,C不重合),以
CE为一直角边作等腰直角三角形ECD,点D在BC的
延长线上,连接BE,AD.
(1)猜想线段BE,AD之间的数量关系及位置关系,直接
写出结论;
(2)现将图①中的△ECD绕点C顺时针旋转n°(090)得到图②,(1)中的结论是否仍然成立?请说明理
A
A
E
EE
B
B
C
D
C
①
2
D
CD
△BCE≌△ACD(SAS),
∴.BE=AD,∠CBE=∠CAD
.·∠CBE+∠ABE+∠BAC=90°
∴.∠CAD+∠ABE+∠BAC=90°,
即∠BAF+∠ABF=90°,
.∠AFB=90°,..BE⊥AD
A
腕解题策略确定“手拉手”模型左右手的关键
E
点:先确定顶点,再找“大腰”和“小腰”.如图,
△BCE和△ACD就是“手拉手”模型:公共顶点
B
是点C,“大腰”分别是BC和AC,“小腰”分别
是CE和CD.
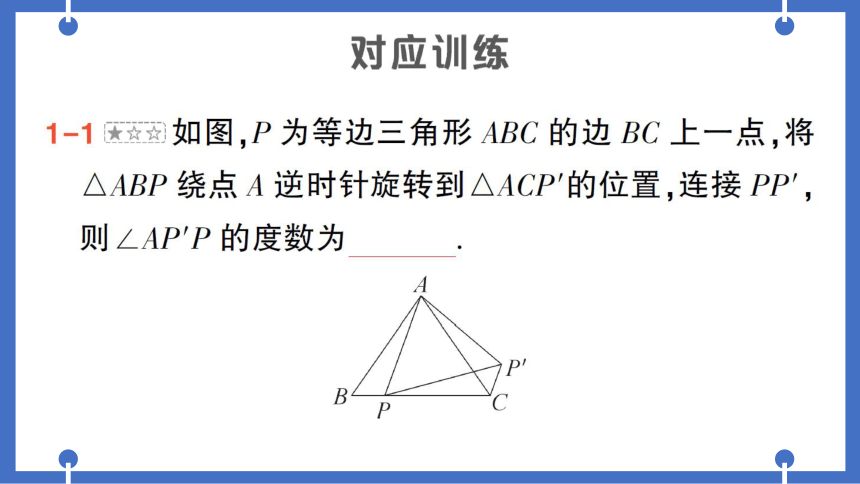
A
P
B
P
C
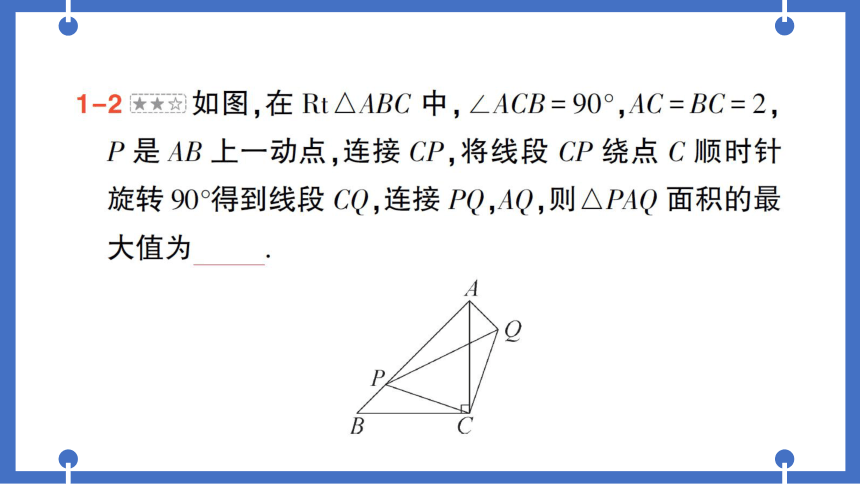
1-2★如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,
P是AB上一动点,连接CP,将线段CP绕点C顺时针
旋转90得到线段CQ,连接PQ,AQ,则△PAQ面积的最
大值为
1
A
2
P
B
C
1-3西[益阳中考]如图,己知△ABC中,∠CAB=20°,
∠ABC=30°,将△ABC绕点A逆时针旋转50°得到
△AB'C',以下结论:①BC=B'C',②AC∥C'B',③C'B”
⊥BB',④∠ABB'=∠ACC',正确的有(B)
A.①②③
B'
B.①2④
C.①③④
A
B
D.②③④
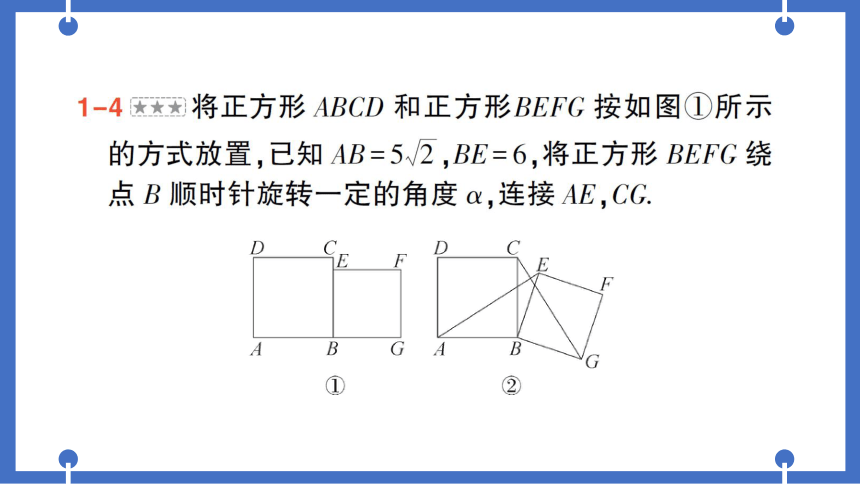
1-4将正方形ABCD和正方形BEFG按如图①所示
的方式放置,己知AB=5√2,BE=6,将正方形BEFG绕
点B顶时针旋转一定的角度α,连接AE,CG.
HE
A
B
G
A
B
①
2
D
C
D
C
E
F
E
F
A
B
G
A
B
G
①
2
解:(1)如图②,设AE,CG交于点H.由题意,得∠ABC=∠EBG=90°,AB
=CB,BE=BG,.∠ABE=∠CBG,.△ABE≌△CBG(SAS),∴.AE=CG,
∠BAE=∠BCG.根据三角形内角和定理,易得∠AHC=∠ABC=90°,∴.AE
⊥CG.
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1
★☆如图①,在等腰直角三角形ABC中,∠ACB
90°,E是边AC上任意一点(点E与点A,C不重合),以
CE为一直角边作等腰直角三角形ECD,点D在BC的
延长线上,连接BE,AD.
(1)猜想线段BE,AD之间的数量关系及位置关系,直接
写出结论;
(2)现将图①中的△ECD绕点C顺时针旋转n°(0
A
A
E
EE
B
B
C
D
C
①
2
D
CD
△BCE≌△ACD(SAS),
∴.BE=AD,∠CBE=∠CAD
.·∠CBE+∠ABE+∠BAC=90°
∴.∠CAD+∠ABE+∠BAC=90°,
即∠BAF+∠ABF=90°,
.∠AFB=90°,..BE⊥AD
A
腕解题策略确定“手拉手”模型左右手的关键
E
点:先确定顶点,再找“大腰”和“小腰”.如图,
△BCE和△ACD就是“手拉手”模型:公共顶点
B
是点C,“大腰”分别是BC和AC,“小腰”分别
是CE和CD.
A
P
B
P
C
1-2★如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,
P是AB上一动点,连接CP,将线段CP绕点C顺时针
旋转90得到线段CQ,连接PQ,AQ,则△PAQ面积的最
大值为
1
A
2
P
B
C
1-3西[益阳中考]如图,己知△ABC中,∠CAB=20°,
∠ABC=30°,将△ABC绕点A逆时针旋转50°得到
△AB'C',以下结论:①BC=B'C',②AC∥C'B',③C'B”
⊥BB',④∠ABB'=∠ACC',正确的有(B)
A.①②③
B'
B.①2④
C.①③④
A
B
D.②③④
1-4将正方形ABCD和正方形BEFG按如图①所示
的方式放置,己知AB=5√2,BE=6,将正方形BEFG绕
点B顶时针旋转一定的角度α,连接AE,CG.
HE
A
B
G
A
B
①
2
D
C
D
C
E
F
E
F
A
B
G
A
B
G
①
2
解:(1)如图②,设AE,CG交于点H.由题意,得∠ABC=∠EBG=90°,AB
=CB,BE=BG,.∠ABE=∠CBG,.△ABE≌△CBG(SAS),∴.AE=CG,
∠BAE=∠BCG.根据三角形内角和定理,易得∠AHC=∠ABC=90°,∴.AE
⊥CG.
同课章节目录
