【同步作业】人教版九(上) 第25章 概率初步 专题十八 概率的综合应用 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 第25章 概率初步 专题十八 概率的综合应用 (课件版) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:30 | ||
图片预览








文档简介
(共22张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
类型
既率与数、方程、不等式的综合
例1
女☆☆
甲、乙两名同学郑一枚骰子
若用字母p,9分别表示两人各投掷一次
的点数,则关于x的方程x2+px+q=0有
两个相等的实数根的概率是(
B
12
1
2
3
4
5
6
q
1
(1,1)(2,1)(3,1)(4,1)
(5,1)(6,1)
2
(1,2)(2,2)(3,2)(4,2)
(5,2)(6,2)
3
(1,3)(2,3)(3,3)(4,3)
(5,3)(6,3)
4
(1,4)(2,4)(3,4)(4,4)
(5,4)(6,4)
5
(1,5)(2,5)
(3,5)(4,5)
(5,5)(6,5)
6
(1,6)(2,6)(3,6)(4,6)
(5,6)
(6,6)
共有36种等可能的结果,使方程有两个
相等的实数根的结果有2种,即p=4,
2
9=4;p=2,9=1.故其概率为
36
18
答案:D
即满足p=4g
1-1「贺州中考]一枚质地均匀的骰子,六个面分别标
有数字1,2,3,4,5,6.连续抛郑骰子两次,第一次正面
朝上的数字作为十位数,第二次正面朝上的数字作为
个位数,则这个两位数能被3整除的概率为
3
1-2☆对现将背面完全相同,正面分别标有数字-6,1,2,
3的4张卡片背面朝上洗匀后,从中任取一张,将该卡
片上的数记为m,再从剩下的3张卡片中任取一张,将
该卡片上的数记为n,则数字m,n都不是方程x2-5x+
6=0的解的概率为
1-3☆有9张卡片,正面分别写有0~8这九个整数,将它
们完全相同的背面朝上洗匀后,任意抽取一张,记卡片上
的数字为m,则能使关于x的分式方程
3x-m=2的解为正
x-1
5
数的概率为
1-4从-2,-1,1,2这四个数中任取一个数作为a的
值,再从余下的三个数中任取一个数作为b的值,则不
等式组
有整数解的既率是
x类型二
既率与函数的综合
无放回抽取
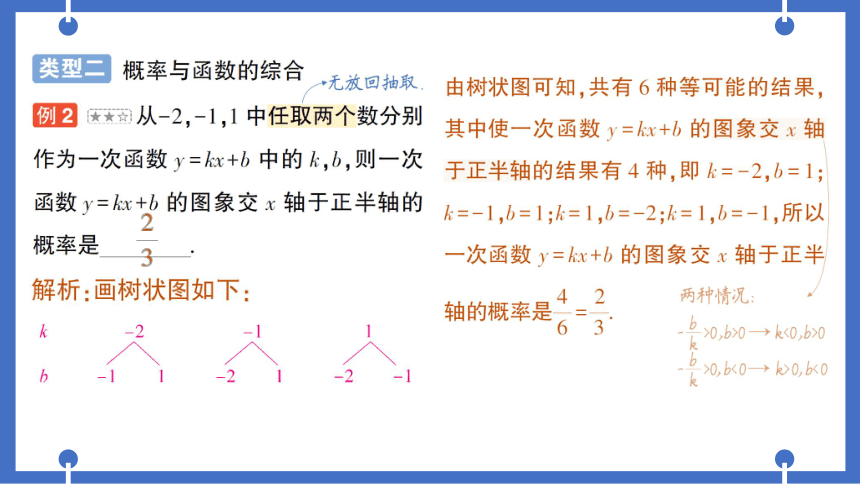
例2
安从-2,-1,1中任取两个数分别
作为一次函数y=x+b中的k,b,则一次
函数y=x+b的图象交x轴于正半轴的
概率是
由树状图可知,共有6种等可能的结果
其中使一次函数y=x+b的图象交x轴
于正半轴的结果有4种,即k=-2,b=1;
k=-1,b=1;k=1,b=-2;k=1,b=-1,所以
一次函数y=x+b的图象交x轴于正半
两种情况:
轴的概率是
-b>0,b>0-→k<0,b>0
2
>0b<0→k>0b0
答案
3
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
类型
既率与数、方程、不等式的综合
例1
女☆☆
甲、乙两名同学郑一枚骰子
若用字母p,9分别表示两人各投掷一次
的点数,则关于x的方程x2+px+q=0有
两个相等的实数根的概率是(
B
12
1
2
3
4
5
6
q
1
(1,1)(2,1)(3,1)(4,1)
(5,1)(6,1)
2
(1,2)(2,2)(3,2)(4,2)
(5,2)(6,2)
3
(1,3)(2,3)(3,3)(4,3)
(5,3)(6,3)
4
(1,4)(2,4)(3,4)(4,4)
(5,4)(6,4)
5
(1,5)(2,5)
(3,5)(4,5)
(5,5)(6,5)
6
(1,6)(2,6)(3,6)(4,6)
(5,6)
(6,6)
共有36种等可能的结果,使方程有两个
相等的实数根的结果有2种,即p=4,
2
9=4;p=2,9=1.故其概率为
36
18
答案:D
即满足p=4g
1-1「贺州中考]一枚质地均匀的骰子,六个面分别标
有数字1,2,3,4,5,6.连续抛郑骰子两次,第一次正面
朝上的数字作为十位数,第二次正面朝上的数字作为
个位数,则这个两位数能被3整除的概率为
3
1-2☆对现将背面完全相同,正面分别标有数字-6,1,2,
3的4张卡片背面朝上洗匀后,从中任取一张,将该卡
片上的数记为m,再从剩下的3张卡片中任取一张,将
该卡片上的数记为n,则数字m,n都不是方程x2-5x+
6=0的解的概率为
1-3☆有9张卡片,正面分别写有0~8这九个整数,将它
们完全相同的背面朝上洗匀后,任意抽取一张,记卡片上
的数字为m,则能使关于x的分式方程
3x-m=2的解为正
x-1
5
数的概率为
1-4从-2,-1,1,2这四个数中任取一个数作为a的
值,再从余下的三个数中任取一个数作为b的值,则不
等式组
有整数解的既率是
x
既率与函数的综合
无放回抽取
例2
安从-2,-1,1中任取两个数分别
作为一次函数y=x+b中的k,b,则一次
函数y=x+b的图象交x轴于正半轴的
概率是
由树状图可知,共有6种等可能的结果
其中使一次函数y=x+b的图象交x轴
于正半轴的结果有4种,即k=-2,b=1;
k=-1,b=1;k=1,b=-2;k=1,b=-1,所以
一次函数y=x+b的图象交x轴于正半
两种情况:
轴的概率是
-b>0,b>0-→k<0,b>0
2
>0b<0→k>0b0
答案
3
同课章节目录
