12.2三角形全等的判定基础练习(含答案)人教版数学八年级上册
文档属性
| 名称 | 12.2三角形全等的判定基础练习(含答案)人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 20:57:53 | ||
图片预览

文档简介
12.2三角形全等的判定基础练习-人教版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
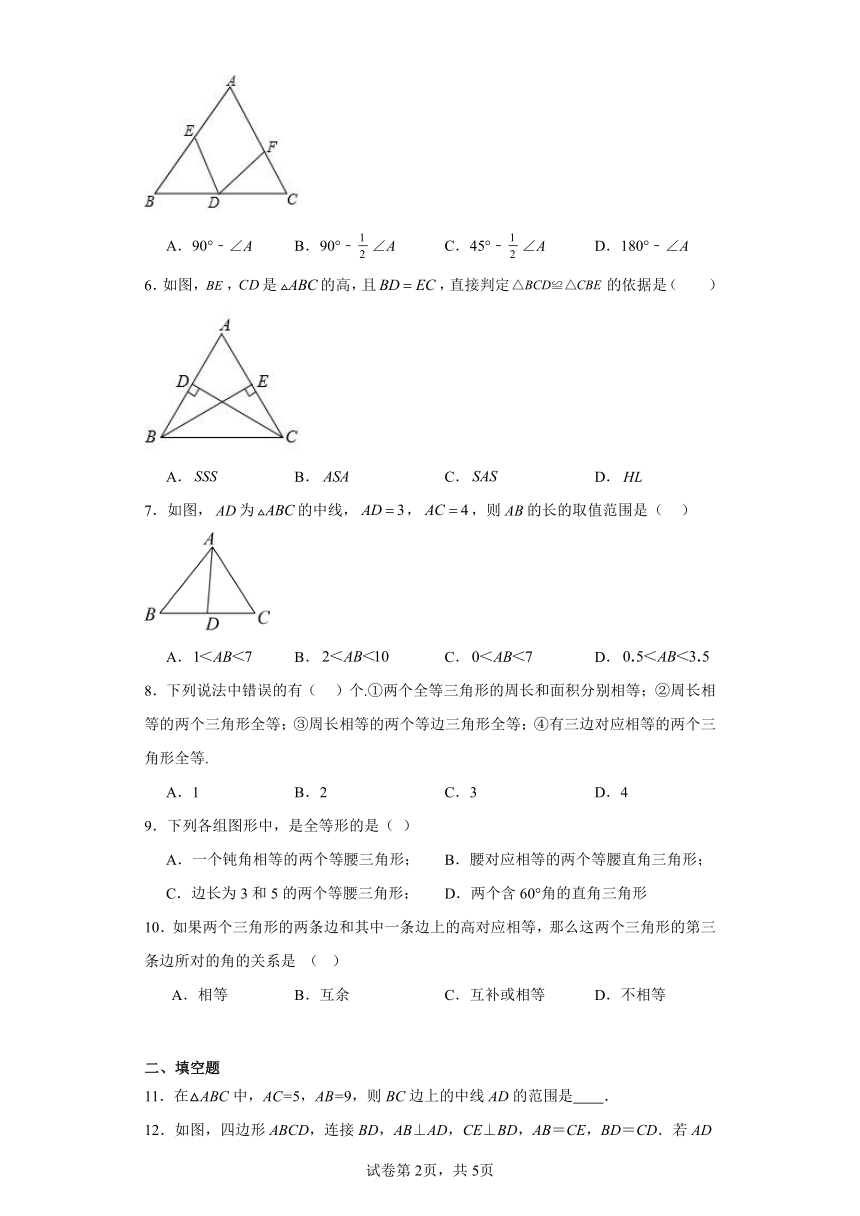
1.如图,已知△ABC的面积为24,BP平分∠ABC,AP⊥BP于点P,并延长AP交BC于点D.则△BPC的面积是( )
A.14 B.12 C.10 D.8
2.满足下列哪种条件时,能判定与全等的是( )
A.,, B.,,
C.,, D.,,
3.如图,在中,,D为中点,,则的度数是( )
A. B. C. D.
4.如图所示,已知∠A=∠D,∠1=∠2,那么要得到△ABC≌△DEF,还应给出的条件是( )
A.∠E=∠B B.ED=BC C.AB=EF D.AF=CD
5.如图,已知在△ABC中,AB=AC,D为BC上一点,BE=CD,CF=BD,那么∠EDF等于( )
A.90°﹣∠A B.90°﹣∠A C.45°﹣∠A D.180°﹣∠A
6.如图,,是的高,且,直接判定的依据是( )
A. B. C. D.
7.如图,为的中线,,,则的长的取值范围是( )
A. B. C. D.
8.下列说法中错误的有( )个.①两个全等三角形的周长和面积分别相等;②周长相等的两个三角形全等;③周长相等的两个等边三角形全等;④有三边对应相等的两个三角形全等.
A.1 B.2 C.3 D.4
9.下列各组图形中,是全等形的是( )
A.一个钝角相等的两个等腰三角形; B.腰对应相等的两个等腰直角三角形;
C.边长为3和5的两个等腰三角形; D.两个含60°角的直角三角形
10.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是 ( )
A.相等 B.互余 C.互补或相等 D.不相等
二、填空题
11.在△ABC中,AC=5,AB=9,则BC边上的中线AD的范围是 .
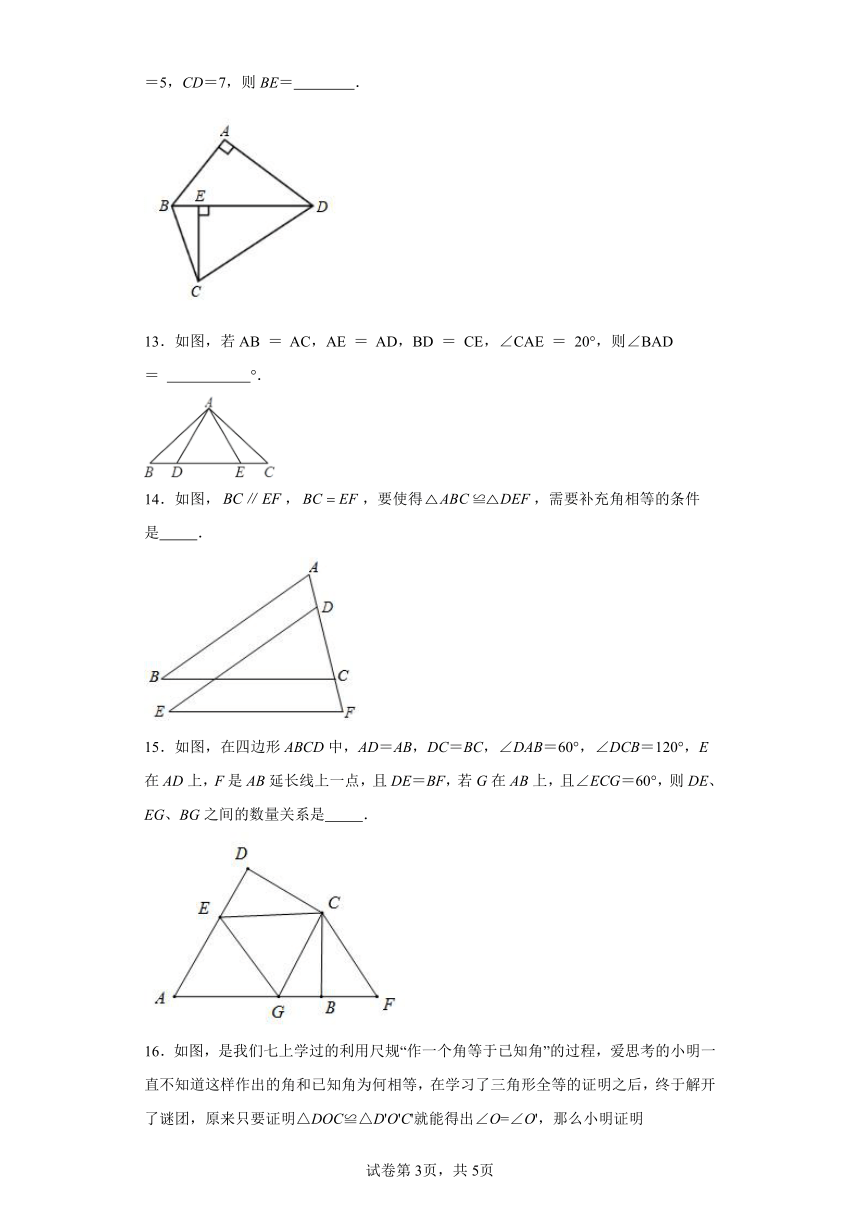
12.如图,四边形ABCD,连接BD,AB⊥AD,CE⊥BD,AB=CE,BD=CD.若AD=5,CD=7,则BE= .
13.如图,若AB = AC,AE = AD,BD = CE,∠CAE = 20°,则∠BAD = °.
14.如图,,,要使得,需要补充角相等的条件是 .
15.如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是 .
16.如图,是我们七上学过的利用尺规“作一个角等于已知角”的过程,爱思考的小明一直不知道这样作出的角和已知角为何相等,在学习了三角形全等的证明之后,终于解开了谜团,原来只要证明△DOC≌△D'O'C'就能得出∠O=∠O',那么小明证明△DOC≌△D'O'C'的依据是 .
17.在四边形ABCD中,AB∥CD,∠A=90,AB=,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为 .
18.给出下列说法:
①如果两条直线被第三条直线所截,那么内错角相等;
②两直角边分别对应相等的两个直角三角形全等;
③一个角的两边与另一个角的两边分别平行,那么这两个角相等;
④过一点有且只有一条直线与已知直线垂直;
⑤过直线外一点向这条直线作的垂线段,叫做这个点到直线的距离.
其中正确的有 个.
19.如图,中,, 分别是上动点,且,当= 时,才能使和全等.
20.如图,E点为△ABC的边AC的中点,CN∥AB,过E点作直线交AB于M点,交CN于N点,若MB=6cm,CN=4cm,则AB= cm.
三、解答题
21.如图,在Rt△ABC中,,,,且交的延长线于E,则与有何关系?说明理由.
22.如图,在中,AD,CE分别是BC、AB边上的高,AD与CE交于点F,连接BF,延长AD到点G,使得,连接BG,若.BF与BG之间有怎样的关系呢?并说明理由.
23.如图,∠ABC=90°,AB=AC,BP是∠ABC中的一条射线,过点C作CD⊥BP,在DC上取DE=DB,连接AE交BP于点F.
(1)找出与∠C相等的角,并证明;
(2)求证:AF=EF;
(3)若,直接写出的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.D
3.A
4.D
5.B
6.D
7.B
8.A
9.B
10.C
11.2<AD<7
12.2
13.20°
14.∠B=∠E或∠A=∠EDF
15.DE+BG=EG
16.SSS
17..
18.
19.3或8
20.10
21.
22.BF=BG.
23.(1)∠C=∠ABP;(2)略;(3).
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知△ABC的面积为24,BP平分∠ABC,AP⊥BP于点P,并延长AP交BC于点D.则△BPC的面积是( )
A.14 B.12 C.10 D.8
2.满足下列哪种条件时,能判定与全等的是( )
A.,, B.,,
C.,, D.,,
3.如图,在中,,D为中点,,则的度数是( )
A. B. C. D.
4.如图所示,已知∠A=∠D,∠1=∠2,那么要得到△ABC≌△DEF,还应给出的条件是( )
A.∠E=∠B B.ED=BC C.AB=EF D.AF=CD
5.如图,已知在△ABC中,AB=AC,D为BC上一点,BE=CD,CF=BD,那么∠EDF等于( )
A.90°﹣∠A B.90°﹣∠A C.45°﹣∠A D.180°﹣∠A
6.如图,,是的高,且,直接判定的依据是( )
A. B. C. D.
7.如图,为的中线,,,则的长的取值范围是( )
A. B. C. D.
8.下列说法中错误的有( )个.①两个全等三角形的周长和面积分别相等;②周长相等的两个三角形全等;③周长相等的两个等边三角形全等;④有三边对应相等的两个三角形全等.
A.1 B.2 C.3 D.4
9.下列各组图形中,是全等形的是( )
A.一个钝角相等的两个等腰三角形; B.腰对应相等的两个等腰直角三角形;
C.边长为3和5的两个等腰三角形; D.两个含60°角的直角三角形
10.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是 ( )
A.相等 B.互余 C.互补或相等 D.不相等
二、填空题
11.在△ABC中,AC=5,AB=9,则BC边上的中线AD的范围是 .
12.如图,四边形ABCD,连接BD,AB⊥AD,CE⊥BD,AB=CE,BD=CD.若AD=5,CD=7,则BE= .
13.如图,若AB = AC,AE = AD,BD = CE,∠CAE = 20°,则∠BAD = °.
14.如图,,,要使得,需要补充角相等的条件是 .
15.如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是 .
16.如图,是我们七上学过的利用尺规“作一个角等于已知角”的过程,爱思考的小明一直不知道这样作出的角和已知角为何相等,在学习了三角形全等的证明之后,终于解开了谜团,原来只要证明△DOC≌△D'O'C'就能得出∠O=∠O',那么小明证明△DOC≌△D'O'C'的依据是 .
17.在四边形ABCD中,AB∥CD,∠A=90,AB=,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为 .
18.给出下列说法:
①如果两条直线被第三条直线所截,那么内错角相等;
②两直角边分别对应相等的两个直角三角形全等;
③一个角的两边与另一个角的两边分别平行,那么这两个角相等;
④过一点有且只有一条直线与已知直线垂直;
⑤过直线外一点向这条直线作的垂线段,叫做这个点到直线的距离.
其中正确的有 个.
19.如图,中,, 分别是上动点,且,当= 时,才能使和全等.
20.如图,E点为△ABC的边AC的中点,CN∥AB,过E点作直线交AB于M点,交CN于N点,若MB=6cm,CN=4cm,则AB= cm.
三、解答题
21.如图,在Rt△ABC中,,,,且交的延长线于E,则与有何关系?说明理由.
22.如图,在中,AD,CE分别是BC、AB边上的高,AD与CE交于点F,连接BF,延长AD到点G,使得,连接BG,若.BF与BG之间有怎样的关系呢?并说明理由.
23.如图,∠ABC=90°,AB=AC,BP是∠ABC中的一条射线,过点C作CD⊥BP,在DC上取DE=DB,连接AE交BP于点F.
(1)找出与∠C相等的角,并证明;
(2)求证:AF=EF;
(3)若,直接写出的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.D
3.A
4.D
5.B
6.D
7.B
8.A
9.B
10.C
11.2<AD<7
12.2
13.20°
14.∠B=∠E或∠A=∠EDF
15.DE+BG=EG
16.SSS
17..
18.
19.3或8
20.10
21.
22.BF=BG.
23.(1)∠C=∠ABP;(2)略;(3).
答案第1页,共2页
答案第1页,共2页
