24.1.4圆周角(第2课时)说课课件
文档属性
| 名称 | 24.1.4圆周角(第2课时)说课课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-13 00:00:00 | ||
图片预览







文档简介
课件21张PPT。圆周角(第二课时)说课稿说课人:金开平兴山县黄粮中学说课内容教材分析教学目标重点难点教学过程反思生成教材分析 圆内接四边形是在研究圆周角之后的学习内容,从圆内接四边形的四个角都是圆周角引入,它是在圆中探求角的相等或互补时常用的一个重要定理,是学生后续学习的基础。 1.?本节课在教材所处的地位和作用:教 学 目 标通过观察图形认识圆内接多边形和多边形的外接圆;探索圆内接四边形的性质定理并运用它探求角之间的关系. 经历圆内接四边形性质定理的探索过程,体会从特殊到一般、数形结合、分类、归纳、转化等数学思想方法,发展学生的推理能力.鼓励学生敢于实践,勇于发现,大胆探索,认识数学的内在联系,增强学习数学的兴趣。 教学目标教学重点教学难点圆内接四边形的性质探索 圆内接四边形的性质探索及应用 教学重点和难点教法与学法教法:演示法,引导启发式教学法 学法:观察、操作与数学思考归纳相结合;自主学习与小组合作探究相结合教学过程课前热身 引入新知如图,点A、B、C、D四点在⊙0上
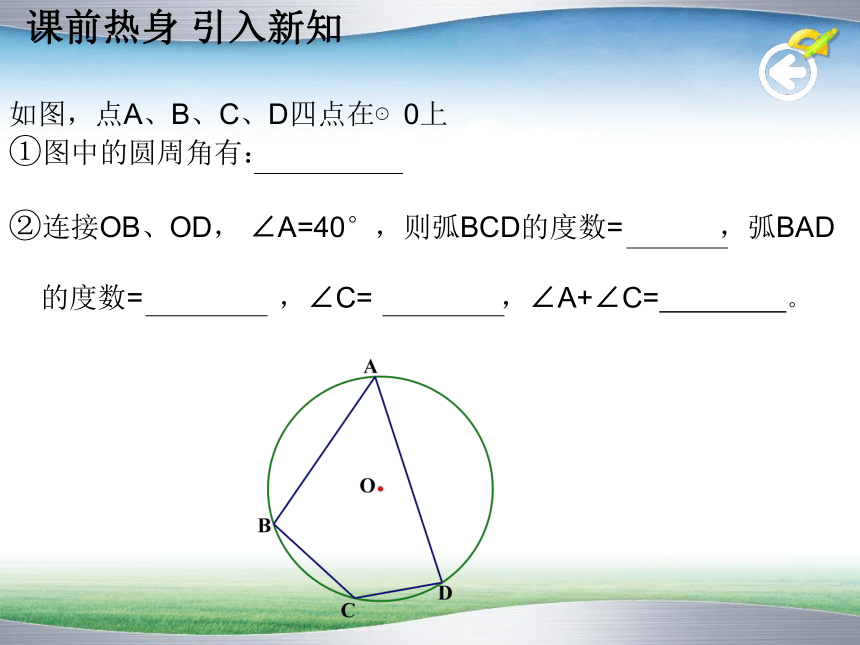
①图中的圆周角有:
②连接OB、OD, ∠A=40°,则弧BCD的度数= ,弧BAD
的度数= ,∠C= ,∠A+∠C= 。
设计意图:
利用第1个问题再认圆周角,利用第2问回忆圆周角定理,并发现∠A与∠C互补,揭示课题,这个问题起到了双重作用,让学生体会到新旧知识的内在联系。合作探究,获取新知1.自读教材:
①如果一个多边形的 都在同一个圆上,这个多边形叫 ,这个圆叫这个多边形的 .
②如图2,四边形ABCD是⊙O的 ,⊙O是四边形ABCD的 .
2.探究性质:
(1)测量:如图2,四边形ABCD是⊙O的内接四边形.
测得∠A= , ∠C= , ∠A+∠C= , 可得∠B+∠D=
(2)画图:在图3的⊙O中画一个圆内接四边形ABCD.
测得∠A= , ∠C= , ∠A+∠C= ,可得∠B+∠D=
(3)猜想:对于任意圆内接四边形,都有∠A+∠C= ,∠B+∠D=
(4)验证:①列表格观察 ②用几何画板验证.
(5)证明:①小组合作,找出证明方法并用语言叙述.
②共同交流证明过程 ③书写证明过程
(6)归纳:圆内接四边形的对角 。 设计意图:
通过对定义的自学培养学生通过观察图形归纳 定义的能力;
通过观察、猜想、度量、画图验证性质培养学生独立获取知识的能力;
通过几何画板的直观演示进一步验证性质,使学生体会从特殊到一般的数学思想方法;
通过小组探究性质的证明过程充分发挥小组的作用,采用兵教兵的方式提高课堂效率,同时使不同层次的学生都能得到发展。师生合作,应用新知例1、如图,四边形ABCD是⊙O的内接四边形,∠CDM是四边形ABCD的一个外角,把∠B叫做∠CDM的内对角.
(1)若∠A=130°,∠B=70°,则∠C= ,∠ADC= ,∠CDM= .
(2)在图4中画出四边形ABCD的外角∠BCN,
则∠BCN的内对角是 .
(3)猜想:∠B与∠CDM的大小有什么关系?
并证明你的猜想.
(4)用一句话叙述(3)中的结论:
圆内接四边形的每一个外角都
等于 。
设计意图:
通过对圆内接四边形性质应用,使学生通过观察图形直接得出圆内接四边形的外角和它的内对角的关系,并独立写出证明过程,进一步归纳圆内接四边形的性质,在不增加教材深度的基础上对教材内容进行拓展,从而使学生体验到成功的喜悦,培养学生解决问题的能力。1. 圆内接平行四边形一定是 形.
2. 若AD是△ABC的外角平分线并交⊙O于点D,连 接BD,CD.
猜想:BD与CD有什么数量关系?
并证明你的猜想.
师生合作,巩固新知 设计意图:学生通过观察图形,并应用圆内接四边形的性质定理找到角之间的关系;通过这两个开放题型对图形的完善,给学生设计小坡度的问题,使学生能应用圆内接四边形的性质证明问题,再一次体验到数学课上成功的喜悦。课堂小结,提炼新知 知识:
方法: 设计意图:
通过学生自主小结,使学生巩固和加深对本节知识的理解和提炼,形成知识体系;并对本节课所用到的数学方法加以总结,进行数学思想方法的渗透。课堂检测,体验成功 (必做)1、如图,四边形ABCD内接于⊙O,∠DCE=70o,则 ∠A= ,∠BOC=
(必做)2、如图,四边形ABCD内接于⊙O,
∠A:∠B:∠C:∠D=1:3:5:x,则x= ,
∠A=
(必做)3、圆内接平行四边形一定是 形.
(选做)4、如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2 交于点D.经过点B的直线EF与⊙O1 交于点E,与⊙O2交于点F。
(1)求证:CE∥DF
(2)变式:若图8中过点A、点B的直线交于⊙O1 内一点,其它条件不变,(1)中结论还成立吗?请你画图证明.设计意图:低起点的分层要求,学生及时检查,查漏补缺;老师及时得到反馈信息,做到堂堂清;有能力的同学通过选做题提升自己的能力 。 板书设计 圆周角(第二课时) 圆内接四边形:
四边形的外接圆:
圆内接四边形的性质:反思成功之处:本节课从回顾圆周角定理及推论入手,引入圆内接四边形的概念和性质的探究,让学生通过自主学习、小组合作的学习方式,经历对圆内接四边形性质定理的画图、观察、猜想、度量验证、推理证明的探索过程,充分发挥学生的主体作用,让学生尽快进入角色,当好演员,演好每一场戏,体验到自主获取新知的乐趣;应用圆内接四边形性质定理时采用变式、变图的方式让学生充分体验作图、观察、猜想进行图形的建构过程,感悟“变”中的“不变”,由于给了分析铺垫,利用几何画板的直观演示突出了重点,突破了难点,整节课学生的参与面广,积极性高,贯穿着积极探究思考的主线,生成了充满活力的课堂,做到了变数学课上“冰冷的美丽”为“火热的思考”,达到了预设目标。 反思不足之处:整个课堂预设是有弹性的、 有留白的预设,给课堂留有很大的包容度和自由度,但由于对学生的了解不够,急于求成,在课堂上给予学生的等待不够;本节课中没能为学生创设一个好的生活情景引入来激发学生的兴趣 ;多媒体的辅助功能发挥得不够好,在今后的教学中应加强学习。
谢谢!
①图中的圆周角有:
②连接OB、OD, ∠A=40°,则弧BCD的度数= ,弧BAD
的度数= ,∠C= ,∠A+∠C= 。
设计意图:
利用第1个问题再认圆周角,利用第2问回忆圆周角定理,并发现∠A与∠C互补,揭示课题,这个问题起到了双重作用,让学生体会到新旧知识的内在联系。合作探究,获取新知1.自读教材:
①如果一个多边形的 都在同一个圆上,这个多边形叫 ,这个圆叫这个多边形的 .
②如图2,四边形ABCD是⊙O的 ,⊙O是四边形ABCD的 .
2.探究性质:
(1)测量:如图2,四边形ABCD是⊙O的内接四边形.
测得∠A= , ∠C= , ∠A+∠C= , 可得∠B+∠D=
(2)画图:在图3的⊙O中画一个圆内接四边形ABCD.
测得∠A= , ∠C= , ∠A+∠C= ,可得∠B+∠D=
(3)猜想:对于任意圆内接四边形,都有∠A+∠C= ,∠B+∠D=
(4)验证:①列表格观察 ②用几何画板验证.
(5)证明:①小组合作,找出证明方法并用语言叙述.
②共同交流证明过程 ③书写证明过程
(6)归纳:圆内接四边形的对角 。 设计意图:
通过对定义的自学培养学生通过观察图形归纳 定义的能力;
通过观察、猜想、度量、画图验证性质培养学生独立获取知识的能力;
通过几何画板的直观演示进一步验证性质,使学生体会从特殊到一般的数学思想方法;
通过小组探究性质的证明过程充分发挥小组的作用,采用兵教兵的方式提高课堂效率,同时使不同层次的学生都能得到发展。师生合作,应用新知例1、如图,四边形ABCD是⊙O的内接四边形,∠CDM是四边形ABCD的一个外角,把∠B叫做∠CDM的内对角.
(1)若∠A=130°,∠B=70°,则∠C= ,∠ADC= ,∠CDM= .
(2)在图4中画出四边形ABCD的外角∠BCN,
则∠BCN的内对角是 .
(3)猜想:∠B与∠CDM的大小有什么关系?
并证明你的猜想.
(4)用一句话叙述(3)中的结论:
圆内接四边形的每一个外角都
等于 。
设计意图:
通过对圆内接四边形性质应用,使学生通过观察图形直接得出圆内接四边形的外角和它的内对角的关系,并独立写出证明过程,进一步归纳圆内接四边形的性质,在不增加教材深度的基础上对教材内容进行拓展,从而使学生体验到成功的喜悦,培养学生解决问题的能力。1. 圆内接平行四边形一定是 形.
2. 若AD是△ABC的外角平分线并交⊙O于点D,连 接BD,CD.
猜想:BD与CD有什么数量关系?
并证明你的猜想.
师生合作,巩固新知 设计意图:学生通过观察图形,并应用圆内接四边形的性质定理找到角之间的关系;通过这两个开放题型对图形的完善,给学生设计小坡度的问题,使学生能应用圆内接四边形的性质证明问题,再一次体验到数学课上成功的喜悦。课堂小结,提炼新知 知识:
方法: 设计意图:
通过学生自主小结,使学生巩固和加深对本节知识的理解和提炼,形成知识体系;并对本节课所用到的数学方法加以总结,进行数学思想方法的渗透。课堂检测,体验成功 (必做)1、如图,四边形ABCD内接于⊙O,∠DCE=70o,则 ∠A= ,∠BOC=
(必做)2、如图,四边形ABCD内接于⊙O,
∠A:∠B:∠C:∠D=1:3:5:x,则x= ,
∠A=
(必做)3、圆内接平行四边形一定是 形.
(选做)4、如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2 交于点D.经过点B的直线EF与⊙O1 交于点E,与⊙O2交于点F。
(1)求证:CE∥DF
(2)变式:若图8中过点A、点B的直线交于⊙O1 内一点,其它条件不变,(1)中结论还成立吗?请你画图证明.设计意图:低起点的分层要求,学生及时检查,查漏补缺;老师及时得到反馈信息,做到堂堂清;有能力的同学通过选做题提升自己的能力 。 板书设计 圆周角(第二课时) 圆内接四边形:
四边形的外接圆:
圆内接四边形的性质:反思成功之处:本节课从回顾圆周角定理及推论入手,引入圆内接四边形的概念和性质的探究,让学生通过自主学习、小组合作的学习方式,经历对圆内接四边形性质定理的画图、观察、猜想、度量验证、推理证明的探索过程,充分发挥学生的主体作用,让学生尽快进入角色,当好演员,演好每一场戏,体验到自主获取新知的乐趣;应用圆内接四边形性质定理时采用变式、变图的方式让学生充分体验作图、观察、猜想进行图形的建构过程,感悟“变”中的“不变”,由于给了分析铺垫,利用几何画板的直观演示突出了重点,突破了难点,整节课学生的参与面广,积极性高,贯穿着积极探究思考的主线,生成了充满活力的课堂,做到了变数学课上“冰冷的美丽”为“火热的思考”,达到了预设目标。 反思不足之处:整个课堂预设是有弹性的、 有留白的预设,给课堂留有很大的包容度和自由度,但由于对学生的了解不够,急于求成,在课堂上给予学生的等待不够;本节课中没能为学生创设一个好的生活情景引入来激发学生的兴趣 ;多媒体的辅助功能发挥得不够好,在今后的教学中应加强学习。
谢谢!
同课章节目录
