数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算(共29张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算(共29张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 22:34:48 | ||
图片预览







文档简介
(共29张PPT)
选择性必修第一册
第一章 空间向量与立体几何
第二章 直线与圆的方程
第三章 圆锥曲线的方程
选择性必修第三册
第六章 计数原理
第七章 随机变里及其分布
第八章 成对数据的统计分析
选择性必修第二册
第四章 数列
第五章 一元函数的导数及其应用
高二数学学习内容
1.理解空间向量的含义,能够区别于平面向量,懂得一些特殊向量如零向量和单位向量。理解相等向量和相反向量,后续进一步理解共面向量和异面向量。
2.掌握空间向量的加法、减法和数乘等线性法则、以及结合律和交换律等运算律,并通过空间几何体加深对运算的理解。培养数形结合思想,发展数学抽象等核心素养。
这是一个做滑翔伞运动的场景.你能想象,在滑翔过程中,飞行员会受到来自哪些不同方向、大小各异的力吗?
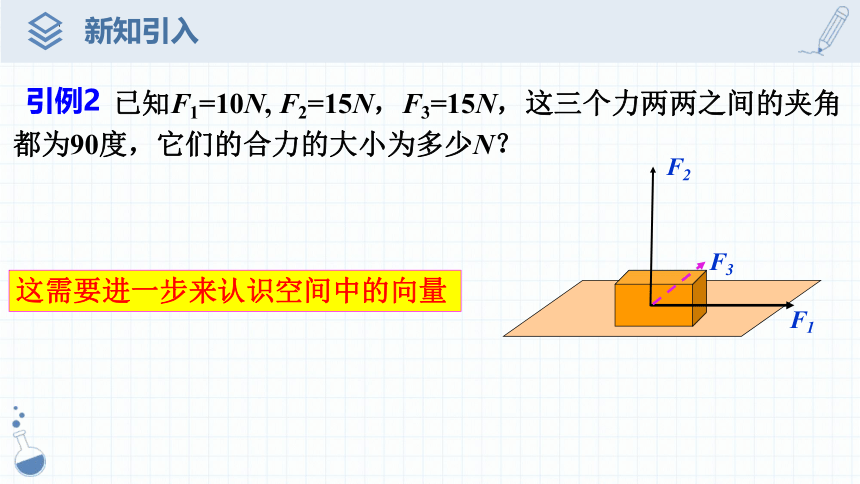
引例1
已知F1=10N, F2=15N,F3=15N,这三个力两两之间的夹角都为90度,它们的合力的大小为多少N?
F3
F1
F2
这需要进一步来认识空间中的向量
引例2
必修 第二册
1.1.1 空间向量及其线性运算
问题1 我们已经学面向量的概念和线性运算,接下来,类比平面向量,给出空间向量的概念和线性运算
平面向量的概念 空间向量的概念
平面内,既有大小又有方向的量,称为平面向量,平面向量的大小叫做向量的长度或模,
空间中,既有大小又有方向的量,称为空间向量,空间向量的大小叫做向量的长度或模,
问1 平面向量的概念是什么?你能类比平面向量给出空间向量的概念吗?
记作 或|a|.
记作 或|a|.
一.空间向量概念
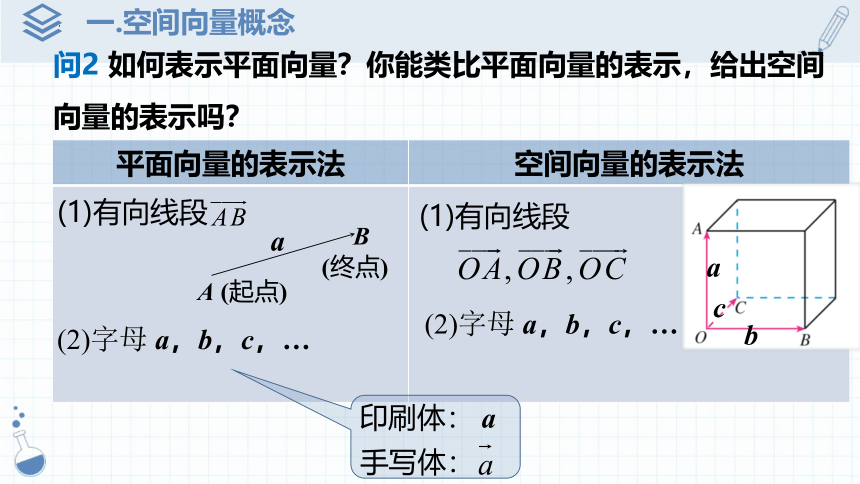
问2 如何表示平面向量?你能类比平面向量的表示,给出空间向量的表示吗?
平面向量的表示法 空间向量的表示法
(1)有向线段
(1)有向线段
A (起点)
B
(终点)
a
(2)字母 a,b,c,…
(2)字母 a,b,c,…
a
c
b
印刷体: a
手写体:
一.空间向量概念
问3 从平面向量的概念出发,我们又学习了不少新的概念.你还记得有哪些吗?你能把这些概念推广到空间向量中吗?
零向量:
单位向量:
相等向量:
相反向量:
共线向量:
模为 1 的向量;
模为 0 的向量,记作 ;零向量的方向任意;
方向相同且模相等的两个向量,记作 ;
与 模相等而方向相反的向量,叫做 的相反向量,记作 ;
一.空间向量概念
平面向量的相关概念 空间向量的相关概念
共线向量:方向相同或相反的两个非零向量,叫做共线向量或平行向量,记作 ;
规定:零向量和任意向量共线.
规定:零向量和任意向量共线.
共线向量:若表示空间向量的有向线段所在直线平行或重合,则这些向量叫做共线向量或平行向量,记作 ;
一.空间向量概念
练习1 判断以下命题的真假:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(4)在正方体 中,必有 ;
(5)若空间向量 满足 ,则 ;
(6)空间中,若 ∥ , ∥ ,则 ∥ ;
(7)空间中任意两个单位向量必相等;
(8)将空间所有单位向量平移到同一个起点,则它们的 终点构成一个圆.
空间任意两个向量都是共面的
由于空间任意两个向量都可以转化为同一个平面内的向量,所以凡涉及空间两个向量的问题,平面向量中的有关结论仍适用于它们.
思考: 空间两条直线可能存在怎样的位置关系?
空间两个向量是否可能异面?
a
b
a
b
O
A
B
向量是自由的,可以进行平移.
问4 平面向量的线性运算有哪些?
二.空间向量的线性运算
问4 平面向量的线性运算有哪些?
平面向量
加法
数乘
三角形法则
平行四边形法则
空间向量
λa,λ为正数,负数,零
减法
三角形法则
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,
这样任意两个空间向量的运算就可以转化为平面向量的运算.
空间向量的线性运算
转化
平面向量的线性运算
二.空间向量的线性运算
a
b
a
b
O
A
B
C
1.空间向量的加减法
二、空间向量的线性运算:
空间向量的加法法则:
三角形法则:首尾相接
平行四边形法则:共起点,对角线
空间向量的减法则:
三角形法则:共起点,减向量的终点指向被减向量的终点
a (λ>0)
a (λ<0)
λ
2.空间向量的数乘:
a
λ
同向
反向
二.空间向量的线性运算
3、加法的运算规律:
简化运算
二.空间向量的线性运算
探究1 如图,在平行六面体ABCD-A'B'C'D'中,分别标出 , 表示的向量. 从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系吗?
A
B
C
D
A'
B'
C'
D'
起点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的体对角线所示向量.
(课本P4 第一段)
【拓展提升】空间向量的线性运算
E
F
同起点的两个平面向量的和向量为平行四边形的对角线所在向量;
同起点的三个空间向量的和向量为平行六面体的体对角线所在向量.
A
B
C
D
E
F
第2题
课本P5
A
B
C
D
E
F
第2题
课本P5
A
B
C
D
图1.1-6
课本P5
A
B
C
D
图1.1-6
课本P5
课本P6-5.如图,已知正方体ABCD A'B'C'D',E,F分别是上底面A'C'和侧面CD'的中心,求下列各式中x,y的值.
课本P5-1.举出一些表示三个不同在一个平面内的向量的实例.
生活中的例子,如墙角的三条棱所在的直线可用于表示三个不同在一个平面内的向量.
A
B
C
D
E
F
(第4题)
课本P5-4.如图,已知四面体ABCD,E,F分别是BC,CD的中点,
化简下列表达式,并在图中标出化简结果的向量.
【考查要点】空间向量的加法法则(平行四边形&三角形法则)、
减法法则(三角形法则)
选择性必修第一册
第一章 空间向量与立体几何
第二章 直线与圆的方程
第三章 圆锥曲线的方程
选择性必修第三册
第六章 计数原理
第七章 随机变里及其分布
第八章 成对数据的统计分析
选择性必修第二册
第四章 数列
第五章 一元函数的导数及其应用
高二数学学习内容
1.理解空间向量的含义,能够区别于平面向量,懂得一些特殊向量如零向量和单位向量。理解相等向量和相反向量,后续进一步理解共面向量和异面向量。
2.掌握空间向量的加法、减法和数乘等线性法则、以及结合律和交换律等运算律,并通过空间几何体加深对运算的理解。培养数形结合思想,发展数学抽象等核心素养。
这是一个做滑翔伞运动的场景.你能想象,在滑翔过程中,飞行员会受到来自哪些不同方向、大小各异的力吗?
引例1
已知F1=10N, F2=15N,F3=15N,这三个力两两之间的夹角都为90度,它们的合力的大小为多少N?
F3
F1
F2
这需要进一步来认识空间中的向量
引例2
必修 第二册
1.1.1 空间向量及其线性运算
问题1 我们已经学面向量的概念和线性运算,接下来,类比平面向量,给出空间向量的概念和线性运算
平面向量的概念 空间向量的概念
平面内,既有大小又有方向的量,称为平面向量,平面向量的大小叫做向量的长度或模,
空间中,既有大小又有方向的量,称为空间向量,空间向量的大小叫做向量的长度或模,
问1 平面向量的概念是什么?你能类比平面向量给出空间向量的概念吗?
记作 或|a|.
记作 或|a|.
一.空间向量概念
问2 如何表示平面向量?你能类比平面向量的表示,给出空间向量的表示吗?
平面向量的表示法 空间向量的表示法
(1)有向线段
(1)有向线段
A (起点)
B
(终点)
a
(2)字母 a,b,c,…
(2)字母 a,b,c,…
a
c
b
印刷体: a
手写体:
一.空间向量概念
问3 从平面向量的概念出发,我们又学习了不少新的概念.你还记得有哪些吗?你能把这些概念推广到空间向量中吗?
零向量:
单位向量:
相等向量:
相反向量:
共线向量:
模为 1 的向量;
模为 0 的向量,记作 ;零向量的方向任意;
方向相同且模相等的两个向量,记作 ;
与 模相等而方向相反的向量,叫做 的相反向量,记作 ;
一.空间向量概念
平面向量的相关概念 空间向量的相关概念
共线向量:方向相同或相反的两个非零向量,叫做共线向量或平行向量,记作 ;
规定:零向量和任意向量共线.
规定:零向量和任意向量共线.
共线向量:若表示空间向量的有向线段所在直线平行或重合,则这些向量叫做共线向量或平行向量,记作 ;
一.空间向量概念
练习1 判断以下命题的真假:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(4)在正方体 中,必有 ;
(5)若空间向量 满足 ,则 ;
(6)空间中,若 ∥ , ∥ ,则 ∥ ;
(7)空间中任意两个单位向量必相等;
(8)将空间所有单位向量平移到同一个起点,则它们的 终点构成一个圆.
空间任意两个向量都是共面的
由于空间任意两个向量都可以转化为同一个平面内的向量,所以凡涉及空间两个向量的问题,平面向量中的有关结论仍适用于它们.
思考: 空间两条直线可能存在怎样的位置关系?
空间两个向量是否可能异面?
a
b
a
b
O
A
B
向量是自由的,可以进行平移.
问4 平面向量的线性运算有哪些?
二.空间向量的线性运算
问4 平面向量的线性运算有哪些?
平面向量
加法
数乘
三角形法则
平行四边形法则
空间向量
λa,λ为正数,负数,零
减法
三角形法则
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,
这样任意两个空间向量的运算就可以转化为平面向量的运算.
空间向量的线性运算
转化
平面向量的线性运算
二.空间向量的线性运算
a
b
a
b
O
A
B
C
1.空间向量的加减法
二、空间向量的线性运算:
空间向量的加法法则:
三角形法则:首尾相接
平行四边形法则:共起点,对角线
空间向量的减法则:
三角形法则:共起点,减向量的终点指向被减向量的终点
a (λ>0)
a (λ<0)
λ
2.空间向量的数乘:
a
λ
同向
反向
二.空间向量的线性运算
3、加法的运算规律:
简化运算
二.空间向量的线性运算
探究1 如图,在平行六面体ABCD-A'B'C'D'中,分别标出 , 表示的向量. 从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系吗?
A
B
C
D
A'
B'
C'
D'
起点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的体对角线所示向量.
(课本P4 第一段)
【拓展提升】空间向量的线性运算
E
F
同起点的两个平面向量的和向量为平行四边形的对角线所在向量;
同起点的三个空间向量的和向量为平行六面体的体对角线所在向量.
A
B
C
D
E
F
第2题
课本P5
A
B
C
D
E
F
第2题
课本P5
A
B
C
D
图1.1-6
课本P5
A
B
C
D
图1.1-6
课本P5
课本P6-5.如图,已知正方体ABCD A'B'C'D',E,F分别是上底面A'C'和侧面CD'的中心,求下列各式中x,y的值.
课本P5-1.举出一些表示三个不同在一个平面内的向量的实例.
生活中的例子,如墙角的三条棱所在的直线可用于表示三个不同在一个平面内的向量.
A
B
C
D
E
F
(第4题)
课本P5-4.如图,已知四面体ABCD,E,F分别是BC,CD的中点,
化简下列表达式,并在图中标出化简结果的向量.
【考查要点】空间向量的加法法则(平行四边形&三角形法则)、
减法法则(三角形法则)
