人教版 八年级上册 13.3等腰三角形复习教案
文档属性
| 名称 | 人教版 八年级上册 13.3等腰三角形复习教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 137.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 23:47:11 | ||
图片预览

文档简介
13.3.等腰三角形复习课
【学习目标】
进一步熟练掌握等腰三角形的性质与判定
进一步掌握等边三角形的性质与判定
进一步掌握含30度角的直角三角形的性质
4、能灵活的根据以上性质和判定解决有关的问题
【重点难点】
重点:等腰三角形的判定和性质及含含30度角的直角三角形的性质
难点:熟练第利用等腰三角形的有关性质和判定解决有关问题
【学习过程】
知识回顾:
等腰三角形的性质
(1)有 相等的三角形叫做等腰三角形.
(2)等腰三角形的两个底角 .
(3)等腰三角形底边上的 、底边上的 、顶角的 三线合一.
(4)等腰三角形是 图形,其对称轴是 .
(5)“如果一个三角形有两个角相等,那么这两个角所对的边也 ”.
2、等边三角形的性质
(1)等边三角形的每个内角都等于 .
(2)如果一个三角形的三个内角都相等,那么这个三角形是 .
(3) 有一个角是60°的等腰三角形是 三角形.
含30度角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的
.(2)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于 .
合作探究:
例1.如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,AB=9,AC=8
求:(1)图中有几个等腰三角形,(说明理由)
(2)△AEF的周长.(说明理由)
例2.如图所示,在Rt△ABC中,∠C=90°,∠BAD= ∠BAC,过点D 作DE⊥AB,DE 恰好是∠ADB的平分线, 求证:CD= DB.
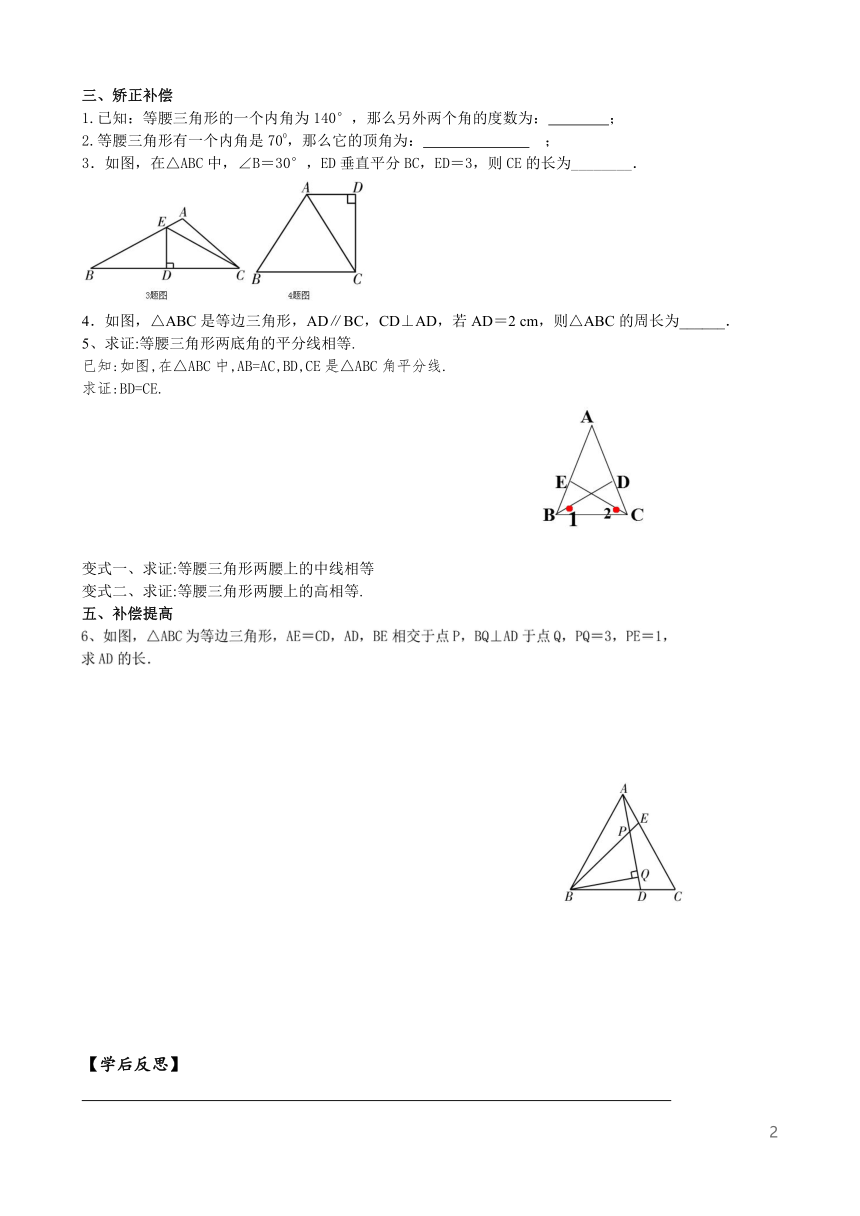
三、矫正补偿
1.已知:等腰三角形的一个内角为140°,那么另外两个角的度数为: ;
2.等腰三角形有一个内角是700,那么它的顶角为: ;
3.如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3,则CE的长为________.
4.如图,△ABC是等边三角形,AD∥BC,CD⊥AD,若AD=2 cm,则△ABC的周长为______.
5、求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.
求证:BD=CE.
变式一、求证:等腰三角形两腰上的中线相等
变式二、求证:等腰三角形两腰上的高相等.
五、补偿提高
6、如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q,PQ=3,PE=1,
求AD的长.
【学后反思】
参考答案:
例题
例1、解:(1)
∵OB为∠ABC的平分线(已知)
∴∠1=∠2 (角平分线的性质)
∵EF∥BC(已知)
∴∠2=∠5(两直线平行,内错角相等)
∴∠1=∠5(等量代换)
∴BE=EO(等角对等边)
∴△EBO为等腰三角形
同理:△FOC也为等腰三角形
(2)∵△AEF周长=AE+AF+EF
∵EF=EO+FO
∴△AEF周长=AE+AF+EO+FO
∵OE=BE(已证)
∵OF=FC(已证)
∴ C△AEF=AE+AF+EB+FC
∵ AB=AE+BE
∵ AC=AF+FC
∴ △AEF周长=AB+AC9+8=17
例2:分析:由条件先证△BED ≌△AED,得∠B=∠CAD=∠DAB,再根据直角三角形的性质,两锐角的和为90°,求得∠B=30°,即可得证.
证明:如图所示,
∵DE⊥AB,
∴∠AED=∠BED=90°,
∵DE是∠ADB的平分线,
∴∠3=∠4,
又∵DE=DE,
∴△BED≌△AED(ASA),
∴AD=BD,∠2=∠B,
∵∠BAD=∠2= ∠BAC/2,
∴∠1=∠2=∠B,
∵AD=BD,∠1+∠2+∠B=90°,
∴∠B=∠1=∠2=30°,
在直角三角形ACD中,
∠1=30°,
∴CD=AD/2=BD/2.
矫正补偿
1、20°、20°;
2、70°、40°
3、6
4、12cm
5、已知:如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.
求证:BD=CE.
证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵∠1=∠ABC/2,
∠2=∠ACB/2(已知),
∴∠1=∠2(等式性质).
在△BDC与△CEB中
∵∠DCB=∠ EBC(已知),
BC=CB(公共边),
∠1=∠2(已证),
∴△BDC≌△CEB(ASA).
∴BD=CE
变式一、已知:如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.
求证:BM=CN.
证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵CM= AC,BN= AB(已知),
∴CM=BN(等式性质).
在△BMC与△CNB中
∵ BC=CB(公共边),
∠MCB=∠NBC(已知),
CM=BN(已证),
∴△BMC≌△CNB(SAS).
∴BM=CN(全等三角形的对应边相等)
变式二、已知:如图,在△ABC中,AB=AC,BP,CQ是△ABC两腰上的高.
求证:BP=CQ.
证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵ BP,CQ是△ABC两腰上的高(已知),
∴∠BPC=∠CQB=900(高的意义).
在△BPC与△CQB中
∵∠BPC=∠CQB(已证),
∠PCB=∠QBC(已证),
BC=CB(公共边),
∴△BPC≌△CQB(AAS).
∴BP=CQ(全等三角形的对应边相等)
拓展提高
6、思路点拨:
∵△ABC为等边三角形,
∴∠BAC=60°,易证△ABE≌△CAD,∴∠ABE=∠DAC,又∵∠BPQ=∠ABE+∠BAP,∴∠BPQ=∠DAC+∠BAP=∠BAC=60°,∴BP=2PQ=6,
BE=BP+PE=7,AD=BE=7
PAGE
1
【学习目标】
进一步熟练掌握等腰三角形的性质与判定
进一步掌握等边三角形的性质与判定
进一步掌握含30度角的直角三角形的性质
4、能灵活的根据以上性质和判定解决有关的问题
【重点难点】
重点:等腰三角形的判定和性质及含含30度角的直角三角形的性质
难点:熟练第利用等腰三角形的有关性质和判定解决有关问题
【学习过程】
知识回顾:
等腰三角形的性质
(1)有 相等的三角形叫做等腰三角形.
(2)等腰三角形的两个底角 .
(3)等腰三角形底边上的 、底边上的 、顶角的 三线合一.
(4)等腰三角形是 图形,其对称轴是 .
(5)“如果一个三角形有两个角相等,那么这两个角所对的边也 ”.
2、等边三角形的性质
(1)等边三角形的每个内角都等于 .
(2)如果一个三角形的三个内角都相等,那么这个三角形是 .
(3) 有一个角是60°的等腰三角形是 三角形.
含30度角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的
.(2)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于 .
合作探究:
例1.如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,AB=9,AC=8
求:(1)图中有几个等腰三角形,(说明理由)
(2)△AEF的周长.(说明理由)
例2.如图所示,在Rt△ABC中,∠C=90°,∠BAD= ∠BAC,过点D 作DE⊥AB,DE 恰好是∠ADB的平分线, 求证:CD= DB.
三、矫正补偿
1.已知:等腰三角形的一个内角为140°,那么另外两个角的度数为: ;
2.等腰三角形有一个内角是700,那么它的顶角为: ;
3.如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3,则CE的长为________.
4.如图,△ABC是等边三角形,AD∥BC,CD⊥AD,若AD=2 cm,则△ABC的周长为______.
5、求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.
求证:BD=CE.
变式一、求证:等腰三角形两腰上的中线相等
变式二、求证:等腰三角形两腰上的高相等.
五、补偿提高
6、如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q,PQ=3,PE=1,
求AD的长.
【学后反思】
参考答案:
例题
例1、解:(1)
∵OB为∠ABC的平分线(已知)
∴∠1=∠2 (角平分线的性质)
∵EF∥BC(已知)
∴∠2=∠5(两直线平行,内错角相等)
∴∠1=∠5(等量代换)
∴BE=EO(等角对等边)
∴△EBO为等腰三角形
同理:△FOC也为等腰三角形
(2)∵△AEF周长=AE+AF+EF
∵EF=EO+FO
∴△AEF周长=AE+AF+EO+FO
∵OE=BE(已证)
∵OF=FC(已证)
∴ C△AEF=AE+AF+EB+FC
∵ AB=AE+BE
∵ AC=AF+FC
∴ △AEF周长=AB+AC9+8=17
例2:分析:由条件先证△BED ≌△AED,得∠B=∠CAD=∠DAB,再根据直角三角形的性质,两锐角的和为90°,求得∠B=30°,即可得证.
证明:如图所示,
∵DE⊥AB,
∴∠AED=∠BED=90°,
∵DE是∠ADB的平分线,
∴∠3=∠4,
又∵DE=DE,
∴△BED≌△AED(ASA),
∴AD=BD,∠2=∠B,
∵∠BAD=∠2= ∠BAC/2,
∴∠1=∠2=∠B,
∵AD=BD,∠1+∠2+∠B=90°,
∴∠B=∠1=∠2=30°,
在直角三角形ACD中,
∠1=30°,
∴CD=AD/2=BD/2.
矫正补偿
1、20°、20°;
2、70°、40°
3、6
4、12cm
5、已知:如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.
求证:BD=CE.
证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵∠1=∠ABC/2,
∠2=∠ACB/2(已知),
∴∠1=∠2(等式性质).
在△BDC与△CEB中
∵∠DCB=∠ EBC(已知),
BC=CB(公共边),
∠1=∠2(已证),
∴△BDC≌△CEB(ASA).
∴BD=CE
变式一、已知:如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.
求证:BM=CN.
证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵CM= AC,BN= AB(已知),
∴CM=BN(等式性质).
在△BMC与△CNB中
∵ BC=CB(公共边),
∠MCB=∠NBC(已知),
CM=BN(已证),
∴△BMC≌△CNB(SAS).
∴BM=CN(全等三角形的对应边相等)
变式二、已知:如图,在△ABC中,AB=AC,BP,CQ是△ABC两腰上的高.
求证:BP=CQ.
证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵ BP,CQ是△ABC两腰上的高(已知),
∴∠BPC=∠CQB=900(高的意义).
在△BPC与△CQB中
∵∠BPC=∠CQB(已证),
∠PCB=∠QBC(已证),
BC=CB(公共边),
∴△BPC≌△CQB(AAS).
∴BP=CQ(全等三角形的对应边相等)
拓展提高
6、思路点拨:
∵△ABC为等边三角形,
∴∠BAC=60°,易证△ABE≌△CAD,∴∠ABE=∠DAC,又∵∠BPQ=∠ABE+∠BAP,∴∠BPQ=∠DAC+∠BAP=∠BAC=60°,∴BP=2PQ=6,
BE=BP+PE=7,AD=BE=7
PAGE
1
