22.3 实际问题与二次函数(3) 课件(共32张PPT)
文档属性
| 名称 | 22.3 实际问题与二次函数(3) 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-31 08:21:26 | ||
图片预览











文档简介
(共32张PPT)
22.3 实际问题与二次函数(3)
人教版九年级上册
知识回顾
O
O
O
O
O
y=ax2
根据函数图象分别设出相应函数解析式
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
y=a(x-x1)(x-x2)
(h,k)
(x1,0)
(x2,0)
教学目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.
2.利用二次函数解决拱桥及运动中的有关问题.
3.能运用二次函数的图象与性质进行决策.
新知导入
日常生活中,我们会看到抛物线形的拱桥
新知探究
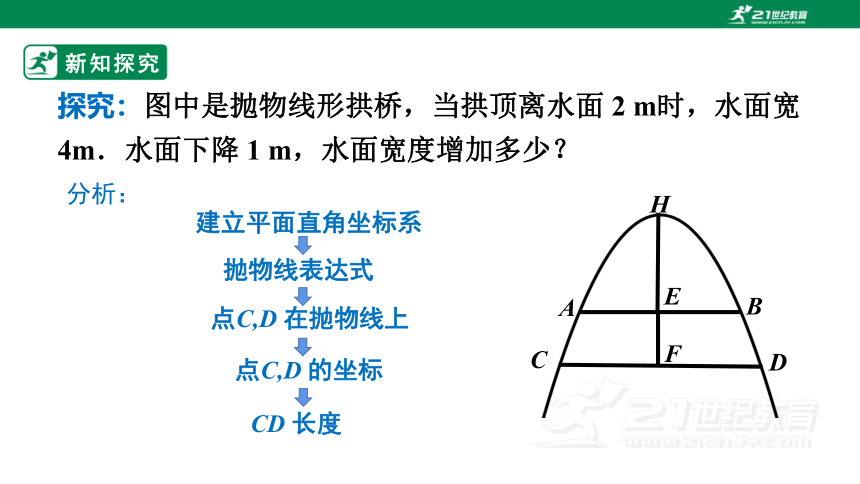
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
F
HE=2
AB=4
EF=1 即 HF=3
CD-AB
E
2m
∴增加的水面宽度=
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
E
F
分析:
CD 长度
点C,D 的坐标
点C,D 在抛物线上
抛物线表达式
建立平面直角坐标系
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
E
F
建立平面直角坐标系需要确定原点,x轴与y轴.
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
解题步骤为:
3.由AB =4,HE =2得
2.可设抛物线的表达式为:
1.以抛物线的顶点H为原点,以抛物线的对称轴为 轴建立平面直角坐标系.
O(H)
A
B
C
D
E
F
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
4.把点 A 或者点 B 坐标代入表达式求 .
5.由HF=3, 得 = ,代入抛物线表达式,
可求得点C,D的横坐标.
6.通过点C,D的横坐标,求得线段CD的长度,计算 CD AB 的值.
O(H)
A
B
C
D
E
F
新知探究
解:
如图,以抛物线的顶点H为原点,抛物线的对称轴为 轴建立平面直角坐标系,可设这条抛物线表示的二次函数为
.
据题意得
新知探究
∵HF=3
新知探究
如图以A为原点,AB所在直线为x轴建立平面直角坐标系。
∵抛物线顶点H坐标为(2,2)
∴可设这条抛物线表示的二次函数为y=a(x-2)2+2,将B(4,0)代入解析式得:
4a+2=0
∴
∵EF=1
新知探究
∴C,D坐标分别是(2),().
∴CD=()-()=
∴CD-AB=
新知探究
解法三:
∵抛物线过 H(0,2),
∴这条抛物线表示的二次函数是
∵EF =1,
把 = 1代入函数解析式得
新知探究
∴C,D坐标分别是(),().
∴CD=-()=
∴CD-AB=
新知小结
通过以上三种解法,我们可以知道解决此类问题要注意以下几点:
要根据实际情况建立适当的平面直角坐标系.
根据平面直角坐标系及已知条件设适当的函数表达式.
建立不同的平面直角坐标系,表达式会有所不同,但计算结果一样.
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
E
F
还有更多解法吗?
图1
图2
图3
图4
y=a(x-h)2+k
新知探究
归纳:
1.图1,图2与前面三种建立平面直角坐标系的方法都是可行的.区别在于计算量的大小.
2.图3,图4不合适,因为此时A,B 是待定的点.
因此建立平面直角坐标系解题要注意以下几点:
1.要使函数表达式形式简洁.
2.容易表达已知点的坐标.
3.便于计算未知点的坐标.
图3
图1
图4
图2
新知练习
练习1:如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形OAB,使顶点O与抛物线的顶点重合,点C,D是抛物线上的点,求外轮廓抛物线解析式.
cm
cm
O
A
B
C
D
解题步骤:
1.以O为原点,过点O作直线AB的平行线和垂线分别作为x轴和y轴建立平面直角坐标系
3.把D(3,-6),代入抛物线表达式求a.
新知练习
cm
cm
O
A
B
C
D
新知典例
例1 某学校九年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时离地面高 m,与篮圈中心的水平距离为7 m,当球出手后水平距离为4 m时到达最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,则他能否获得成功?
新知典例
解:(1)由题意可知,抛物线经过点(0, ),顶点坐标是(4,4),篮圈中心的坐标是(7,3).
设抛物线的解析式是y=a(x-4)2+4,
∴ =16a+4
解得:a=
∴抛物线解析式为y= (x-4)2+4.
当x=7时,y= ×(7-4)2+4=3,
∴篮圈的中心点在抛物线上,
(2)∵当x=1时,y= ×(1-4)2+4=3<3.1,
∴能够盖帽拦截成功.
∴能够投中.
新知练习
练习2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在 O 点正上方 1 m 的 P 处发出一球,羽毛球飞行的高度 y(m) 与水平距离 x(m) 之间满足函数解析式 y=a(x-4)2+h,已知点 O 与球网的水平距离为 5 m,球网的高度为 1.55 m.
(1)当a=-时,①求 h 的值;②通过计算判断此球能否过网;
解:(1) ① 当a=时,y=(x-4)2+h,
将点P(0,1)代入,得×16+h=1,
解得h= .
新知练习
解:(1) ② 把x=5代入y=(x-4)2+,
得y=×(5-4)2+=1.625,
∵1.625>1.55,∴此球能过网.
练习2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在 O 点正上方 1 m 的 P 处发出一球,羽毛球飞行的高度 y(m) 与水平距离 x(m) 之间满足函数解析式 y=a(x-4)2+h,已知点 O 与球网的水平距离为 5 m,球网的高度为 1.55 m.
(1)当a=-时,①求 h 的值;②通过计算判断此球能否过网;
新知练习
解:(2) 把(0,1),(7,)代入y=a(x-4)2+h,
得 解得∴a=.
练习2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在 O 点正上方 1 m 的 P 处发出一球,羽毛球飞行的高度 y(m) 与水平距离 x(m) 之间满足函数解析式 y=a(x-4)2+h,已知点 O 与球网的水平距离为 5 m,球网的高度为 1.55 m.
(2)若甲发球过网后,羽毛球飞行到与点 O 的水平距离为 7 m,离地面的高度为 m 的 Q 处时,乙扣球成功,求 a 的值.
课堂总结
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线型问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
对接中考
1.发射一枚炮弹,经过 x 秒后炮弹的高度为 y 米,x,y 满足 y=ax2+bx,其中 a,b 是常数,且 a≠0.若此炮弹在第 6 秒与第 14 秒时的高度相等,则炮弹达到最大高度的时刻是( )
B
A.第8秒 B.第10秒
C.第12秒 D.第15秒
解:∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+=10,
即炮弹达到最大高度的时刻是第10 秒.
对接中考
2.拱桥呈抛物线形,其函数解析式为 y= - x2,当拱桥下水面宽为 12 m 时,水面离拱桥顶端的高度是( )
D
A.3 m B.2 m
C.4 m D.9 m
解:由题意可得x=6时,y=-×62=-9.
故水面离拱桥顶端的高度是9 m.
对接中考
3.一位篮球运动员在距离篮圈中心水平距离 4 m 处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为 2.5 m 时,达到最大高度 3.5 m,然后准确落入篮框内,已知篮圈中心距离地面高度为 3.05 m,在如图所示的平面直角坐标系中,下列说法正确的是 ( )
A
A.此抛物线的解析式是 y=-x2 +3.5
B.篮圈中心的坐标是 (4,3.05)
C.此抛物线的顶点坐标是 (3.5,0)
D.篮球出手时离地面的高度是 2 m
对接中考
解:选项A中,∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数解析式为y=ax2+3.5,
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入得 3.05=a×1.52+3.5,∴a=-0.2,∴y=-0.2x2+3.5,故本选项正确;
选项B中,由图示知,篮圈中心的坐标是(1.5,3.05),故本选项错误;
选项C中,由图示知,此抛物线的顶点坐标是(0,3.5),故本选项错误;
选项D中,设这次跳投时,球出手处离地面h m,
∵由选项A可知y=-0.2x2+3.5,∴当x=-2.5时,h=-0.2×(-2.5)2+3.5=2.25.
∴这次跳投时,球出手处离地面2.25 m.故本选项错误.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
22.3 实际问题与二次函数(3)
人教版九年级上册
知识回顾
O
O
O
O
O
y=ax2
根据函数图象分别设出相应函数解析式
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
y=a(x-x1)(x-x2)
(h,k)
(x1,0)
(x2,0)
教学目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.
2.利用二次函数解决拱桥及运动中的有关问题.
3.能运用二次函数的图象与性质进行决策.
新知导入
日常生活中,我们会看到抛物线形的拱桥
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
F
HE=2
AB=4
EF=1 即 HF=3
CD-AB
E
2m
∴增加的水面宽度=
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
E
F
分析:
CD 长度
点C,D 的坐标
点C,D 在抛物线上
抛物线表达式
建立平面直角坐标系
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
E
F
建立平面直角坐标系需要确定原点,x轴与y轴.
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
解题步骤为:
3.由AB =4,HE =2得
2.可设抛物线的表达式为:
1.以抛物线的顶点H为原点,以抛物线的对称轴为 轴建立平面直角坐标系.
O(H)
A
B
C
D
E
F
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
4.把点 A 或者点 B 坐标代入表达式求 .
5.由HF=3, 得 = ,代入抛物线表达式,
可求得点C,D的横坐标.
6.通过点C,D的横坐标,求得线段CD的长度,计算 CD AB 的值.
O(H)
A
B
C
D
E
F
新知探究
解:
如图,以抛物线的顶点H为原点,抛物线的对称轴为 轴建立平面直角坐标系,可设这条抛物线表示的二次函数为
.
据题意得
新知探究
∵HF=3
新知探究
如图以A为原点,AB所在直线为x轴建立平面直角坐标系。
∵抛物线顶点H坐标为(2,2)
∴可设这条抛物线表示的二次函数为y=a(x-2)2+2,将B(4,0)代入解析式得:
4a+2=0
∴
∵EF=1
新知探究
∴C,D坐标分别是(2),().
∴CD=()-()=
∴CD-AB=
新知探究
解法三:
∵抛物线过 H(0,2),
∴这条抛物线表示的二次函数是
∵EF =1,
把 = 1代入函数解析式得
新知探究
∴C,D坐标分别是(),().
∴CD=-()=
∴CD-AB=
新知小结
通过以上三种解法,我们可以知道解决此类问题要注意以下几点:
要根据实际情况建立适当的平面直角坐标系.
根据平面直角坐标系及已知条件设适当的函数表达式.
建立不同的平面直角坐标系,表达式会有所不同,但计算结果一样.
新知探究
探究:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽4m.水面下降 1 m,水面宽度增加多少?
H
A
B
C
D
E
F
还有更多解法吗?
图1
图2
图3
图4
y=a(x-h)2+k
新知探究
归纳:
1.图1,图2与前面三种建立平面直角坐标系的方法都是可行的.区别在于计算量的大小.
2.图3,图4不合适,因为此时A,B 是待定的点.
因此建立平面直角坐标系解题要注意以下几点:
1.要使函数表达式形式简洁.
2.容易表达已知点的坐标.
3.便于计算未知点的坐标.
图3
图1
图4
图2
新知练习
练习1:如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形OAB,使顶点O与抛物线的顶点重合,点C,D是抛物线上的点,求外轮廓抛物线解析式.
cm
cm
O
A
B
C
D
解题步骤:
1.以O为原点,过点O作直线AB的平行线和垂线分别作为x轴和y轴建立平面直角坐标系
3.把D(3,-6),代入抛物线表达式求a.
新知练习
cm
cm
O
A
B
C
D
新知典例
例1 某学校九年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时离地面高 m,与篮圈中心的水平距离为7 m,当球出手后水平距离为4 m时到达最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,则他能否获得成功?
新知典例
解:(1)由题意可知,抛物线经过点(0, ),顶点坐标是(4,4),篮圈中心的坐标是(7,3).
设抛物线的解析式是y=a(x-4)2+4,
∴ =16a+4
解得:a=
∴抛物线解析式为y= (x-4)2+4.
当x=7时,y= ×(7-4)2+4=3,
∴篮圈的中心点在抛物线上,
(2)∵当x=1时,y= ×(1-4)2+4=3<3.1,
∴能够盖帽拦截成功.
∴能够投中.
新知练习
练习2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在 O 点正上方 1 m 的 P 处发出一球,羽毛球飞行的高度 y(m) 与水平距离 x(m) 之间满足函数解析式 y=a(x-4)2+h,已知点 O 与球网的水平距离为 5 m,球网的高度为 1.55 m.
(1)当a=-时,①求 h 的值;②通过计算判断此球能否过网;
解:(1) ① 当a=时,y=(x-4)2+h,
将点P(0,1)代入,得×16+h=1,
解得h= .
新知练习
解:(1) ② 把x=5代入y=(x-4)2+,
得y=×(5-4)2+=1.625,
∵1.625>1.55,∴此球能过网.
练习2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在 O 点正上方 1 m 的 P 处发出一球,羽毛球飞行的高度 y(m) 与水平距离 x(m) 之间满足函数解析式 y=a(x-4)2+h,已知点 O 与球网的水平距离为 5 m,球网的高度为 1.55 m.
(1)当a=-时,①求 h 的值;②通过计算判断此球能否过网;
新知练习
解:(2) 把(0,1),(7,)代入y=a(x-4)2+h,
得 解得∴a=.
练习2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在 O 点正上方 1 m 的 P 处发出一球,羽毛球飞行的高度 y(m) 与水平距离 x(m) 之间满足函数解析式 y=a(x-4)2+h,已知点 O 与球网的水平距离为 5 m,球网的高度为 1.55 m.
(2)若甲发球过网后,羽毛球飞行到与点 O 的水平距离为 7 m,离地面的高度为 m 的 Q 处时,乙扣球成功,求 a 的值.
课堂总结
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线型问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
对接中考
1.发射一枚炮弹,经过 x 秒后炮弹的高度为 y 米,x,y 满足 y=ax2+bx,其中 a,b 是常数,且 a≠0.若此炮弹在第 6 秒与第 14 秒时的高度相等,则炮弹达到最大高度的时刻是( )
B
A.第8秒 B.第10秒
C.第12秒 D.第15秒
解:∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+=10,
即炮弹达到最大高度的时刻是第10 秒.
对接中考
2.拱桥呈抛物线形,其函数解析式为 y= - x2,当拱桥下水面宽为 12 m 时,水面离拱桥顶端的高度是( )
D
A.3 m B.2 m
C.4 m D.9 m
解:由题意可得x=6时,y=-×62=-9.
故水面离拱桥顶端的高度是9 m.
对接中考
3.一位篮球运动员在距离篮圈中心水平距离 4 m 处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为 2.5 m 时,达到最大高度 3.5 m,然后准确落入篮框内,已知篮圈中心距离地面高度为 3.05 m,在如图所示的平面直角坐标系中,下列说法正确的是 ( )
A
A.此抛物线的解析式是 y=-x2 +3.5
B.篮圈中心的坐标是 (4,3.05)
C.此抛物线的顶点坐标是 (3.5,0)
D.篮球出手时离地面的高度是 2 m
对接中考
解:选项A中,∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数解析式为y=ax2+3.5,
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入得 3.05=a×1.52+3.5,∴a=-0.2,∴y=-0.2x2+3.5,故本选项正确;
选项B中,由图示知,篮圈中心的坐标是(1.5,3.05),故本选项错误;
选项C中,由图示知,此抛物线的顶点坐标是(0,3.5),故本选项错误;
选项D中,设这次跳投时,球出手处离地面h m,
∵由选项A可知y=-0.2x2+3.5,∴当x=-2.5时,h=-0.2×(-2.5)2+3.5=2.25.
∴这次跳投时,球出手处离地面2.25 m.故本选项错误.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
