人教版数学八年级上册 15.2分式的运算第2课时 分式的加减 课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 15.2分式的运算第2课时 分式的加减 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 657.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-31 08:52:13 | ||
图片预览




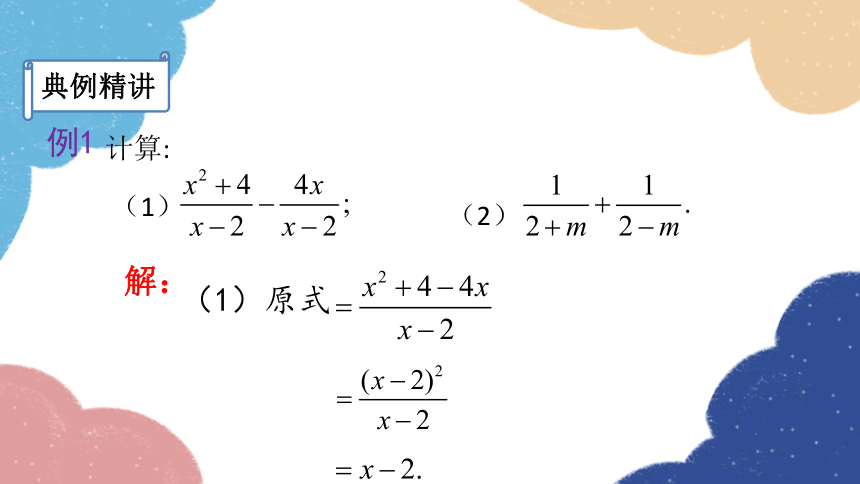
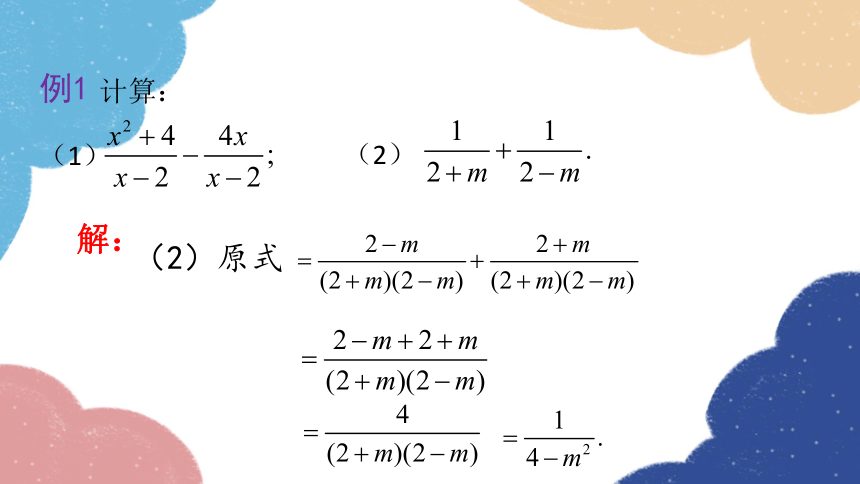

文档简介
(共20张PPT)
15.2 分式的运算
第2课时 分式的加减
1.掌握分式的加减法的法则,能熟练进行分式的
加减运算.
2.能熟练进行分式的混合运算.
教学目标
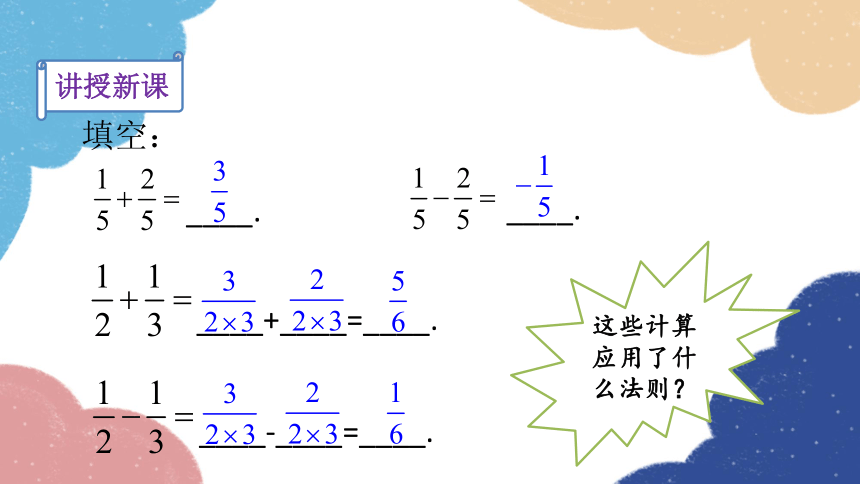
填空:
____+____=____.
____-____=____.
____.
____.
讲授新课
这些计算应用了什么法则?
类比刚才的算法,填写下面的空:
____+____=
____-____=
____.
____.
你能总结出分式的加减法则吗?
分式的加减法则:
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
上述法则可用式子表示为
例1
计算:
(1)
(2)
解:
(1)原式
典例精讲
例1
计算:
(1)
(2)
解:
(2)原式
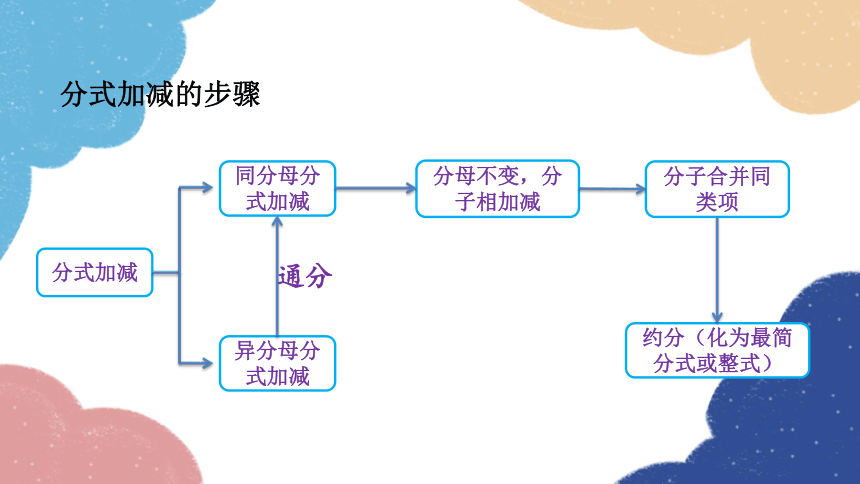
分式加减的步骤
分式加减
约分(化为最简分式或整式)
分子合并同类项
分母不变,分子相加减
同分母分式加减
异分母分式加减
通分
例2
计算
解:
原式
分式与数有相
同的混合运算
顺序:先乘方,
再乘除,然后
加减.
典例精讲
例3
计算
典例精讲
解:
原式
解:
原式
对于分式的混合运算:
(1)运算顺序:先乘方,再乘除,然后加减,有括号的先算括号里面的;
(2)注意各分式中分子、分母符号的处理.当结果的分子或分母是负数时,负号提到分式本身的前面.
(3)计算结果要化为最简分式.
知识归纳
例4 有一条小船顺流航行50km后,又立即返回原地.如果船在静
水中的速度为akm/h,水流的速度为8km/h,那么顺流航行比逆
流航行少用多少时间?
分析:先求出顺流速度,再求出逆流速度,根据
时间=路程÷速度
分别求出逆流航行时间、顺流航行时间,相减即可得出
顺流航行比逆流航行少用的时间.
典例精讲
解:
依题意有
(小时)
答:顺流航行比逆流航行少用
小时.
例4 有一条小船顺流航行50km后,又立即返回原地.如果船在静
水中的速度为akm/h,水流的速度为8km/h,那么顺流航行比逆
流航行少用多少时间?
1.化简 的结果是 _______.
2.计算 的结果是_______.
3.计算的 结果是________.
课堂巩固
4.计算:
解:
原式
5.计算:
原式
解:
1.分式的加减法则
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
课堂小结
2.分式的混合运算的顺序
分式的混合运算的顺序是先算乘方,再算乘除,
最后算加减,有括号的先算括号里面的,计算
结果要化为最简分式或整式.
15.2 分式的运算
第2课时 分式的加减
1.掌握分式的加减法的法则,能熟练进行分式的
加减运算.
2.能熟练进行分式的混合运算.
教学目标
填空:
____+____=____.
____-____=____.
____.
____.
讲授新课
这些计算应用了什么法则?
类比刚才的算法,填写下面的空:
____+____=
____-____=
____.
____.
你能总结出分式的加减法则吗?
分式的加减法则:
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
上述法则可用式子表示为
例1
计算:
(1)
(2)
解:
(1)原式
典例精讲
例1
计算:
(1)
(2)
解:
(2)原式
分式加减的步骤
分式加减
约分(化为最简分式或整式)
分子合并同类项
分母不变,分子相加减
同分母分式加减
异分母分式加减
通分
例2
计算
解:
原式
分式与数有相
同的混合运算
顺序:先乘方,
再乘除,然后
加减.
典例精讲
例3
计算
典例精讲
解:
原式
解:
原式
对于分式的混合运算:
(1)运算顺序:先乘方,再乘除,然后加减,有括号的先算括号里面的;
(2)注意各分式中分子、分母符号的处理.当结果的分子或分母是负数时,负号提到分式本身的前面.
(3)计算结果要化为最简分式.
知识归纳
例4 有一条小船顺流航行50km后,又立即返回原地.如果船在静
水中的速度为akm/h,水流的速度为8km/h,那么顺流航行比逆
流航行少用多少时间?
分析:先求出顺流速度,再求出逆流速度,根据
时间=路程÷速度
分别求出逆流航行时间、顺流航行时间,相减即可得出
顺流航行比逆流航行少用的时间.
典例精讲
解:
依题意有
(小时)
答:顺流航行比逆流航行少用
小时.
例4 有一条小船顺流航行50km后,又立即返回原地.如果船在静
水中的速度为akm/h,水流的速度为8km/h,那么顺流航行比逆
流航行少用多少时间?
1.化简 的结果是 _______.
2.计算 的结果是_______.
3.计算的 结果是________.
课堂巩固
4.计算:
解:
原式
5.计算:
原式
解:
1.分式的加减法则
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
课堂小结
2.分式的混合运算的顺序
分式的混合运算的顺序是先算乘方,再算乘除,
最后算加减,有括号的先算括号里面的,计算
结果要化为最简分式或整式.
