化学人教版(2019)选择性必修第一册 1.2.1盖斯定律及其应用课件(共38张PPT)
文档属性
| 名称 | 化学人教版(2019)选择性必修第一册 1.2.1盖斯定律及其应用课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2023-08-31 12:09:08 | ||
图片预览









文档简介
(共38张PPT)
第一章 化学反应的热效应
第二节 反应热的计算
第一课时 盖斯定律
在化学科研中,经常要通过实验测定物质在发生时化学反应所放出或吸收的热量。但是某些物质的反应热,由于种种原因不能直接测得,只能通过化学计算的方式间接获得。在生产中,对燃料的燃烧、反应条件的控制以及废热的利用,也需要反应热计算 。
【思考】
C的燃烧,很难控制C只生成CO而不继续生成CO2,C(s)+ O2(g)=CO(g)因此这个反应的ΔH无法直接测得。但这个反应的反应热是冶金工业中非常有用的数据,应该如何获得呢?能否利用一些已知反应的反应热来计算其他反应的反应热呢?
答案自然是肯定的
应用盖斯定律,可间接地把它的反应热计算出来。
1840年,盖斯(G.H. Hess,俄国化学家)从大量的实验事实中总结出一条规律:化学反应不管是一步完成还是分几步完成,其反应热是相同的。也就是说,化学反应的反应热只与反应的始态(各反应物)和终态
(各生成物)有关,而与具体反应进行的途径无关。
如果一个反应可以分几步进行,则各分步反应的
反应热之和与该反应一步完成时的反应热是相同的,
这就是盖斯定律。
用这一定律可以从已精确测定的反应的热效应来计算难于测量或不能测量的反应的热效应。
【化学史料】
一.盖斯定律
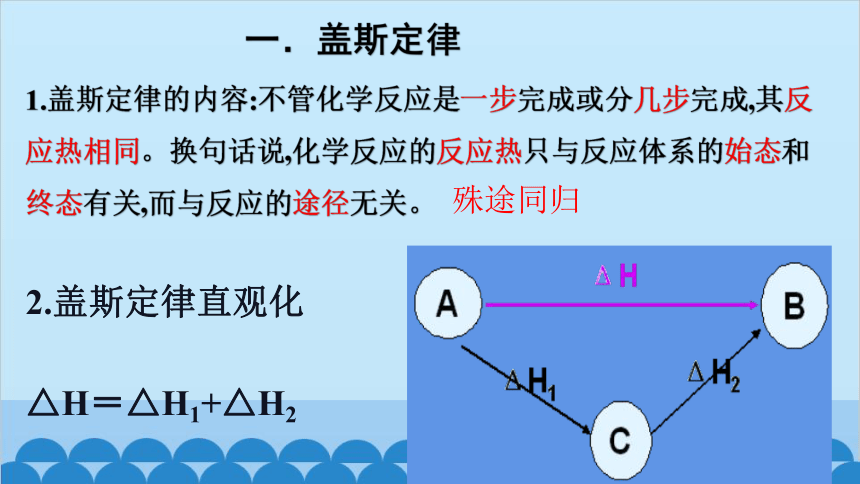
1.盖斯定律的内容:不管化学反应是一步完成或分几步完成,其反应热相同。换句话说,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。
2.盖斯定律直观化
△H=△H1+△H2
殊途同归
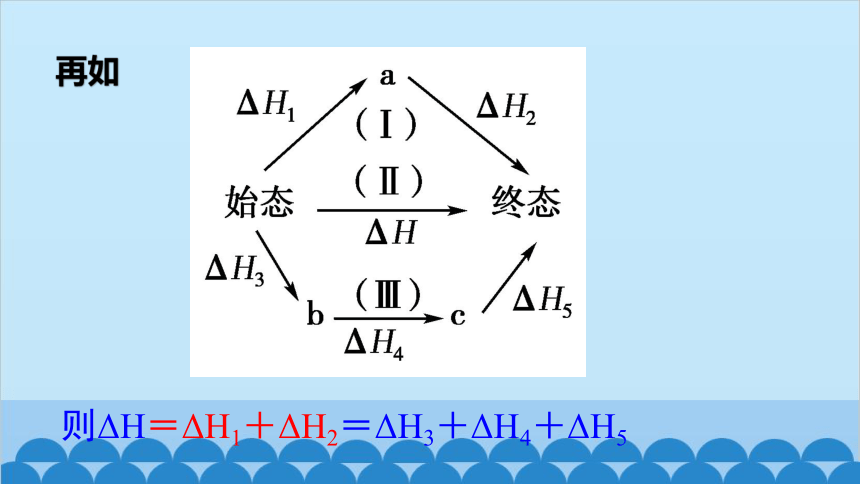
则ΔH=ΔH1+ΔH2=ΔH3+ΔH4+ΔH5
再如
如同山的绝对高度与上山的途径无关一样,A点相当于反应体系的始态,B点相当于反应体系的终态,山的高度相当于化学反应的反应热。同一起点登山至山顶,不管选哪一条路走,历经不同的途径和不同的方式,但山的高度是不变的。
3.理解
(1)途径角度
终态(L)
始态(S)
反应热
经过一个循环,体系仍处于S态,因为物质没有发生变化,所以就不能引发能量变化,即 H1+ H2=0
先从始态S变化到终态L 体系放出热量( H1 <0)
始态(S)
然后从L到S,体系吸收热量( H2>0)
终态(L)
推论:同一个热化学反应方程式,正向反应 H1与逆向反应 H2大小相等,符号相反,即: H1= – H2
(2)能量守恒角度
△H1 +△H2 ≡ 0
能量的吸收和释放是以发生变化的物质为基础的,两者密不可分,但以物质为主。如果物质没有变化,就不能引起能量的变化,前者为因,后者为果。
对于任意一个反应,无论该反应从什么途径发生,从反应开始到反应结束,能量既不增加,也不减少,只是从一种形式转化成另一种形式
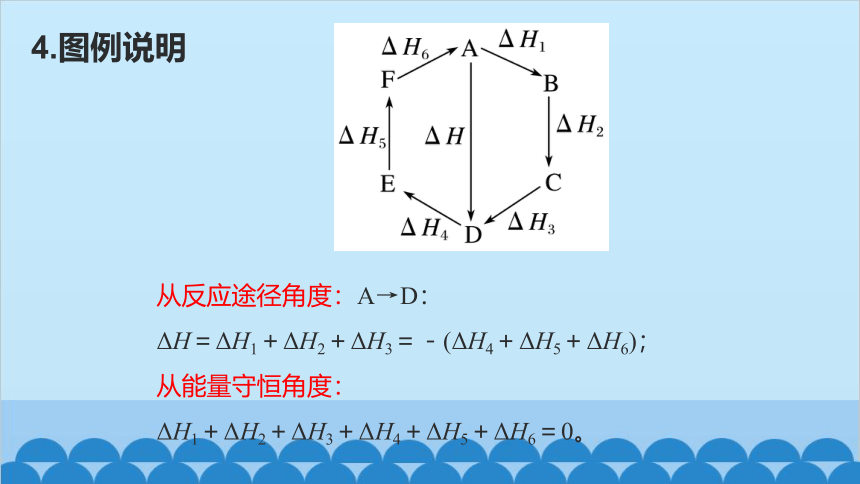
4.图例说明
从反应途径角度:A→D:
ΔH=ΔH1+ΔH2+ΔH3=-(ΔH4+ΔH5+ΔH6);
从能量守恒角度:
ΔH1+ΔH2+ΔH3+ΔH4+ΔH5+ΔH6=0。
【例1】下列关于盖斯定律描述不正确的是( )
A.化学反应的反应热不仅与反应体系的始态和终态有关,也与反应的途径有关
B.盖斯定律遵守能量守恒定律
C.利用盖斯定律可间接计算通过实验难测定的反应的反应热
D.利用盖斯定律可以计算有副反应发生的反应的反应热
A
【例2】已知在298 K时下述反应的有关数据:
C(s)+1/2O2(g)===CO(g) ΔH1=-110.5 kJ·mol-1
C(s)+O2(g)===CO2(g) ΔH2=-393.5 kJ·mol-1,
则C(s)+CO2(g)===2CO(g)的ΔH为( )
A.+283.5 kJ·mol-1 B.+172.5 kJ·mol-1
C.-172.5 kJ·mol-1 D.-504 kJ·mol-1
【解析】 ①2C(s)+O2(g)===2CO(g) ΔH3=-221 kJ·mol-1②CO2(g)===C(s)+O2(g) ΔH4=+393.5 kJ·mol-1利用盖斯定律,①+②可得C(s)+CO2(g)===2CO(g) ΔH=-221 kJ·mol-1+393.5 kJ·mol-1=+172.5 kJ·mol-1。
B
5、盖斯定律在科学研究中的重要意义:
有些反应进行得很慢;
有些反应不容易直接发生;
有些反应的产品不纯(有副反应发生)。
这些都给测量反应热造成了困难,利用盖斯定律可以间接地把它们的反应热计算出来
上述三个反应具有如下关系:
C(s)+O2(g)
CO2(g)
H1
H3
H2
途径一
途径二
根据盖斯定律,则有:
=-393.5kJ/mol-(-283.0kJ/mol)
=-110.5kJ/mol
H1= H2+ H3
H3= H1- H2
下列数据表示H2的燃烧热吗?Why?
H2(g)+1/2O2(g) = H2O (g)
△H1=-241.8kJ/mol
H2O(g) = H2O (l)
△H2=-44 kJ/mol
已知
H2(g)+1/2O2(g) = H2O (l)
△H=△H1+ △H2=-285.8kJ/mol
实例1
同素异形体相互转化但反应热相当小而且转化速率慢,有时还很不完全,测定反应热很困难。现在可根据盖斯提出的观点“不管化学反应是一步完成或分几步完成,这个总过程的热效应是相同的”。已知:
P4(s、白磷)+5O2(g)=P4O10(s); = -2983.2 kJ/mol
H1
P(s、红磷)+5/4O2(g)=1/4P4O10(s); = -738.5 kJ/mol
H2
试写出白磷转化为红磷的热化学方程式
_________________________________。
P4(白磷、s) = 4 P(红磷、s); = -29.2 kJ/mol
H
实例2
①-4×②:
有些化学反应进行很慢或不易直接发生,很难直接测得这些反应的反应热,可通过盖斯定律获得它们的反应热数据。
二.盖斯定律的应用
①虚拟路径法
若反应物A变为生成物D,可以有两种途径:
(a)由A直接变成D,反应热为ΔH;
(b)由A经过B变成C,再由C变成D,每步的反应热分别为ΔH1、ΔH2、ΔH3。
如图所示:
则有:ΔH=ΔH1+ΔH2+ΔH3
C(s)+ O2(g)
CO2(g)
△H1
△H3
△H1= △H2 + △H3
CO(g) + O2(g)
1
2
△H2
△H3 =△H1 - △H2
C(s) + O2(g) = CO(g) △H3=?
CO(g)+ O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s) + O2(g) = CO2(g) △H1=-393.5 kJ/mol
+)
△H3 =△H1 - △H2
= -393.5 kJ/mol -(-283.0 kJ/mol)
= -110.5 kJ/mol
1
2
1
2
C(s) + O2(g) = CO(g) △H3= -110.5 kJ/mol
1
2
②加合法
即运用所给热化学方程式通过加减的方法得到所求热化学方程式。
关键:目标方程式的“四则运算式”的导出(消元法)
方法:写出目标方程式确定“过渡物质” (要消去的物质)然后用消元法逐一消去“过渡物质”,导出“四则运算式”。
根据盖斯定律书写热化学方程式的方法:
(1)确定待求反应的热化学方程式;
(2)找出待求热化学方程式中各物质出现在已知方程式中的位置(是同侧还是异侧);
(3)利用同侧相加、异侧相减进行处理;
(4)根据未知方程式中各物质的化学计量数通过乘除来调整已知反应的化学计量数,并消去中间产物;
(5)实施叠加并确定反应热的变化。
①热化学方程式中物质的化学计量数同乘以某一数时,反应热数值也必须乘以该数;
②热化学方程式相加减时,同种物质之间可相加减,反应热也随之相加减;
③将一个热化学方程式颠倒时,△H的数值不变,但“+”、“—”号必须随之改变;
④若热化学方程式相减,最好能先把被减方程式进行颠倒,然后相加,更不易出错。
应用盖斯定律计算反应热应注意:
【例1】已知① CO(g) + 1/2 O2(g) = CO2(g) ; ΔH1= -283.0 kJ/mol
② H2(g) + 1/2 O2(g) = H2O(l) ; ΔH2= -285.8 kJ/mol
③C2H5OH(l) + 3 O2(g) = 2 CO2(g) + 3H2O(l);
ΔH3=-1370 kJ/mol
试计算: ④ 2CO(g)+ 4 H2(g) = H2O(l)+ C2H5OH (l) 的ΔH
【解】:①×2 + ②×4 - ③ = ④
ΔH=ΔH1×2 +ΔH2×4 -ΔH3
=-283.2×2 -285.8×4 +1370 =-339.2 kJ/mol
【例2】 已知:①H2O(g)===H2O(l) ΔH1=Q1 kJ·mol-1
②C2H5OH(g)===C2H5OH(l) ΔH2=Q2 kJ·mol-1
③C2H5OH(g)+3O2(g)===2CO2(g)+3H2O(g)
ΔH3=Q3 kJ·mol-1
则反应C2H5OH(l)+3O2(g)===2CO2(g)+3H2O(l)的反应热ΔH为( )
A.(Q1+Q2+Q3) kJ·mol-1 B.(3Q1+Q2+Q3) kJ·mol-1
C.(Q1-3Q2+Q3) kJ·mol-1 D.(3Q1-Q2+Q3) kJ·mol-1
【解析】 本题考查对盖斯定律的理解和应用,解答此类问题的常用方法有虚拟途径法和加合法两种,具体求算如下:
(1)设计反应的虚拟过程如下:
则有ΔH=-ΔH2+ΔH3+3ΔH1
=(-Q2+Q3+3Q1) kJ·mol-1。
(2)根据盖斯定律(加合法),令①×3+③-②,
整理得C2H5OH(l)+3O2(g)===2CO2(g)+3H2O(l)
ΔH=3ΔH1+ΔH3-ΔH2=(3Q1+Q3-Q2) kJ·mol-1。
【答案】 D
例3:写出石墨变成金刚石的热化学方程式 (25℃,101kPa时)
查燃烧热表知:
①C(石墨,s)+O2(g)= CO2(g) △H1=-393.5kJ/mol
②C(金刚石,s)+O2(g)= CO2(g) △H2=-395.0kJ/mol
解:①- ②得:
C(石墨,s)= C(金刚石,s) ; △H=+1.5kJ/mol
练习1:已知下列各反应的焓变
①Ca(s)+C(s,石墨)+3/2O2(g)=CaCO3(s) △H1 = -1206.8 kJ/mol
②Ca(s)+1/2O2(g)=CaO(s) △H2= -635.1 kJ/mol
③C(s,石墨)+O2(g)=CO2(g) △H3 = -393.5 kJ/mol
试求④CaCO3(s)=CaO(s)+CO2(g)的焓变
△H4=+178.2kJ/mol
④=②+③-①
练习2:按照盖斯定律,结合下述反应方程式回答问题,已知:
①NH3(g)+HCl(g)=NH4Cl(s) △H1=-176kJ/mol
②NH3(g)+H2O(l)=NH3(aq) △H2=-35.1kJ/mol
③HCl(g) +H2O(l)=HCl(aq) △H3=-72.3kJ/mol
④NH3(aq)+ HCl(aq)=NH4Cl(aq) △H4=-52.3kJ/mol
⑤NH4Cl(s)+2H2O(l)= NH4Cl(aq) △H5=?
则第⑤个方程式中的反应热△H是________。
根据盖斯定律和上述反应方程式得:
⑤=④+③+②-①,
即△H5 = +16.3kJ/mol
“三步”确定热化学方程式或ΔH
找出
调整
加和
根据待求解的热化学方程式中的反应物和生成物找出可用的已知热化学方程式。
①根据待求解的热化学方程式调整可用热化学方程式的方向,同时调整△H的符号。
②根据待求解的热化学方程式将调整好的热化学方程式进行缩小或扩大相应的倍数,同时调整△H的值。
将调整好的热化学方程式和△H分别进行求△H加和。确定目标反应的焓变△H。
1.判断正误(正确的打“√”,错误的打“×”)(1)一个反应一步完成或分几步完成,两者相比,经过的步骤越多,放出的热量越多。 ( )(2)化学反应的反应热与化学反应的始态有关,与终态无关。
( )(3)同一反应的反应热ΔH与化学计量数成正比。 ( )
(3)利用盖斯定律,可计算某些反应的反应热。 ( )
(4)任何化学反应的反应热都可以直接测定。 ( )
×
×
√
√
×
2.下列说法不正确的是( )
①在热化学方程式中无论是反应物还是生成物都必须标明状态 ②所有的化学反应都伴随着能量变化 ③放热反应发生时不必加热 ④吸热反应在加热后才能发生 ⑤化学反应的热效应数值只与参加反应的物质的多少有关 ⑥一般来说,吸热反应在一定条件下也能发生 ⑦根据盖斯定律,反应焓变的大小与反应的途径有关,无论是一步完成还是分几步完成,其总的热效应完全相同
A.②③⑥⑦ B.③④⑤⑦ C.④⑤⑦ D.①③④⑦
B
【解析】放热反应有时需要加热才能实现,如燃烧反应,③错误;有些吸热反应不需要加热就能发生,如铵盐与Ba(OH)2混合研磨就能反应,④错误;化学反应的热效应不仅与反应物的多少有关,还与物质的状态有关,⑤错误;从盖斯定律来看,反应焓变的大小与途径无关,故⑦错误。
3.能源问题是人类社会面临的重大课题,H2、CO、CH3OH都是重要的能源物质,它们的燃烧热依次为285.8 kJ·mol-1、282.5 kJ·mol-1、726.7 kJ·mol-1。已知CO和H2在一定条件下可以合成甲醇CO(g)+2H2(g)===CH3OH(l)。则CO与H2反应合成甲醇的热化学方程式为( )
A.CO(g)+2H2(g)===CH3OH(l) ΔH=-127.4 kJ·mol-1
B.CO(g)+2H2(g)===CH3OH(l) ΔH=+127.4 kJ·mol-1
C.CO(g)+2H2(g)===CH3OH(g) ΔH=-127.4 kJ·mol-1
D.CO(g)+2H2(g)===CH3OH(g) ΔH=+127.4 kJ·mol-1
【解析】 根据题给三种物质的燃烧热可以写出:
H2(g)+1/2O2(g)===H2O(l) ΔH1=-285.8 kJ·mol-1①
CO(g)+1/2O2(g)===CO2(g) ΔH2=-282.5 kJ·mol-1②
CH3OH(l)+3/2O2(g)===CO2(g)+2H2O(l) ΔH3=-726.7 kJ·mol-1③
运用盖斯定律进行计算,即①×2+②-③可得:
CO(g)+2H2(g)===CH3OH(l) ΔH=2ΔH1+ΔH2-ΔH3
=2×(-285.8 kJ·mol-1)+(-282.5 kJ·mol-1)-(-726.7 kJ·mol-1)=-127.4 kJ·mol-1。
A
4.化学反应N2(g)+3H2(g)===2NH3(l)的能量变化如图所示,该反应的ΔH等于( )
A.+2(a-b-c) kJ·mol-1 B.+2(b-a) kJ·mol-1
C.+(b+c-a) kJ·mol-1 D.+(a+b) kJ·mol-1
【解析】 由题图知N2(g)+H2(g)===NH3(l)
需放出(b+c-a)kJ的热量,
故N2(g)+3H2(g)===2NH3(l) ΔH=-2(b+c-a) kJ·mol-1 =2(a-b-c) kJ·mol-1 ,A项正确。
A
小 结
一、盖斯定律
1、定义:
不管化学反应是一步完成或分几步完成,其反应热是相同。
2、特点:
反应的热效应只与始终态有关,与反应途径无关。
正、逆反应的反应热数值相等,符号相反。
3、影响反应热的因素:
温度、压强,物质状态,反应物用量等。
4、应用:
间接计算难以直接测定的反应热。
关键:
目标方程式的“四则运算式”的导出。
方法:
写出目标方程式确定“过渡物质” (要消去的物质)然后用消元法逐一消去“过渡物质”,导出“四则运算式”。
途径:
①虚拟路径法; ②加合法。
第一章 化学反应的热效应
第二节 反应热的计算
第一课时 盖斯定律
在化学科研中,经常要通过实验测定物质在发生时化学反应所放出或吸收的热量。但是某些物质的反应热,由于种种原因不能直接测得,只能通过化学计算的方式间接获得。在生产中,对燃料的燃烧、反应条件的控制以及废热的利用,也需要反应热计算 。
【思考】
C的燃烧,很难控制C只生成CO而不继续生成CO2,C(s)+ O2(g)=CO(g)因此这个反应的ΔH无法直接测得。但这个反应的反应热是冶金工业中非常有用的数据,应该如何获得呢?能否利用一些已知反应的反应热来计算其他反应的反应热呢?
答案自然是肯定的
应用盖斯定律,可间接地把它的反应热计算出来。
1840年,盖斯(G.H. Hess,俄国化学家)从大量的实验事实中总结出一条规律:化学反应不管是一步完成还是分几步完成,其反应热是相同的。也就是说,化学反应的反应热只与反应的始态(各反应物)和终态
(各生成物)有关,而与具体反应进行的途径无关。
如果一个反应可以分几步进行,则各分步反应的
反应热之和与该反应一步完成时的反应热是相同的,
这就是盖斯定律。
用这一定律可以从已精确测定的反应的热效应来计算难于测量或不能测量的反应的热效应。
【化学史料】
一.盖斯定律
1.盖斯定律的内容:不管化学反应是一步完成或分几步完成,其反应热相同。换句话说,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。
2.盖斯定律直观化
△H=△H1+△H2
殊途同归
则ΔH=ΔH1+ΔH2=ΔH3+ΔH4+ΔH5
再如
如同山的绝对高度与上山的途径无关一样,A点相当于反应体系的始态,B点相当于反应体系的终态,山的高度相当于化学反应的反应热。同一起点登山至山顶,不管选哪一条路走,历经不同的途径和不同的方式,但山的高度是不变的。
3.理解
(1)途径角度
终态(L)
始态(S)
反应热
经过一个循环,体系仍处于S态,因为物质没有发生变化,所以就不能引发能量变化,即 H1+ H2=0
先从始态S变化到终态L 体系放出热量( H1 <0)
始态(S)
然后从L到S,体系吸收热量( H2>0)
终态(L)
推论:同一个热化学反应方程式,正向反应 H1与逆向反应 H2大小相等,符号相反,即: H1= – H2
(2)能量守恒角度
△H1 +△H2 ≡ 0
能量的吸收和释放是以发生变化的物质为基础的,两者密不可分,但以物质为主。如果物质没有变化,就不能引起能量的变化,前者为因,后者为果。
对于任意一个反应,无论该反应从什么途径发生,从反应开始到反应结束,能量既不增加,也不减少,只是从一种形式转化成另一种形式
4.图例说明
从反应途径角度:A→D:
ΔH=ΔH1+ΔH2+ΔH3=-(ΔH4+ΔH5+ΔH6);
从能量守恒角度:
ΔH1+ΔH2+ΔH3+ΔH4+ΔH5+ΔH6=0。
【例1】下列关于盖斯定律描述不正确的是( )
A.化学反应的反应热不仅与反应体系的始态和终态有关,也与反应的途径有关
B.盖斯定律遵守能量守恒定律
C.利用盖斯定律可间接计算通过实验难测定的反应的反应热
D.利用盖斯定律可以计算有副反应发生的反应的反应热
A
【例2】已知在298 K时下述反应的有关数据:
C(s)+1/2O2(g)===CO(g) ΔH1=-110.5 kJ·mol-1
C(s)+O2(g)===CO2(g) ΔH2=-393.5 kJ·mol-1,
则C(s)+CO2(g)===2CO(g)的ΔH为( )
A.+283.5 kJ·mol-1 B.+172.5 kJ·mol-1
C.-172.5 kJ·mol-1 D.-504 kJ·mol-1
【解析】 ①2C(s)+O2(g)===2CO(g) ΔH3=-221 kJ·mol-1②CO2(g)===C(s)+O2(g) ΔH4=+393.5 kJ·mol-1利用盖斯定律,①+②可得C(s)+CO2(g)===2CO(g) ΔH=-221 kJ·mol-1+393.5 kJ·mol-1=+172.5 kJ·mol-1。
B
5、盖斯定律在科学研究中的重要意义:
有些反应进行得很慢;
有些反应不容易直接发生;
有些反应的产品不纯(有副反应发生)。
这些都给测量反应热造成了困难,利用盖斯定律可以间接地把它们的反应热计算出来
上述三个反应具有如下关系:
C(s)+O2(g)
CO2(g)
H1
H3
H2
途径一
途径二
根据盖斯定律,则有:
=-393.5kJ/mol-(-283.0kJ/mol)
=-110.5kJ/mol
H1= H2+ H3
H3= H1- H2
下列数据表示H2的燃烧热吗?Why?
H2(g)+1/2O2(g) = H2O (g)
△H1=-241.8kJ/mol
H2O(g) = H2O (l)
△H2=-44 kJ/mol
已知
H2(g)+1/2O2(g) = H2O (l)
△H=△H1+ △H2=-285.8kJ/mol
实例1
同素异形体相互转化但反应热相当小而且转化速率慢,有时还很不完全,测定反应热很困难。现在可根据盖斯提出的观点“不管化学反应是一步完成或分几步完成,这个总过程的热效应是相同的”。已知:
P4(s、白磷)+5O2(g)=P4O10(s); = -2983.2 kJ/mol
H1
P(s、红磷)+5/4O2(g)=1/4P4O10(s); = -738.5 kJ/mol
H2
试写出白磷转化为红磷的热化学方程式
_________________________________。
P4(白磷、s) = 4 P(红磷、s); = -29.2 kJ/mol
H
实例2
①-4×②:
有些化学反应进行很慢或不易直接发生,很难直接测得这些反应的反应热,可通过盖斯定律获得它们的反应热数据。
二.盖斯定律的应用
①虚拟路径法
若反应物A变为生成物D,可以有两种途径:
(a)由A直接变成D,反应热为ΔH;
(b)由A经过B变成C,再由C变成D,每步的反应热分别为ΔH1、ΔH2、ΔH3。
如图所示:
则有:ΔH=ΔH1+ΔH2+ΔH3
C(s)+ O2(g)
CO2(g)
△H1
△H3
△H1= △H2 + △H3
CO(g) + O2(g)
1
2
△H2
△H3 =△H1 - △H2
C(s) + O2(g) = CO(g) △H3=?
CO(g)+ O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s) + O2(g) = CO2(g) △H1=-393.5 kJ/mol
+)
△H3 =△H1 - △H2
= -393.5 kJ/mol -(-283.0 kJ/mol)
= -110.5 kJ/mol
1
2
1
2
C(s) + O2(g) = CO(g) △H3= -110.5 kJ/mol
1
2
②加合法
即运用所给热化学方程式通过加减的方法得到所求热化学方程式。
关键:目标方程式的“四则运算式”的导出(消元法)
方法:写出目标方程式确定“过渡物质” (要消去的物质)然后用消元法逐一消去“过渡物质”,导出“四则运算式”。
根据盖斯定律书写热化学方程式的方法:
(1)确定待求反应的热化学方程式;
(2)找出待求热化学方程式中各物质出现在已知方程式中的位置(是同侧还是异侧);
(3)利用同侧相加、异侧相减进行处理;
(4)根据未知方程式中各物质的化学计量数通过乘除来调整已知反应的化学计量数,并消去中间产物;
(5)实施叠加并确定反应热的变化。
①热化学方程式中物质的化学计量数同乘以某一数时,反应热数值也必须乘以该数;
②热化学方程式相加减时,同种物质之间可相加减,反应热也随之相加减;
③将一个热化学方程式颠倒时,△H的数值不变,但“+”、“—”号必须随之改变;
④若热化学方程式相减,最好能先把被减方程式进行颠倒,然后相加,更不易出错。
应用盖斯定律计算反应热应注意:
【例1】已知① CO(g) + 1/2 O2(g) = CO2(g) ; ΔH1= -283.0 kJ/mol
② H2(g) + 1/2 O2(g) = H2O(l) ; ΔH2= -285.8 kJ/mol
③C2H5OH(l) + 3 O2(g) = 2 CO2(g) + 3H2O(l);
ΔH3=-1370 kJ/mol
试计算: ④ 2CO(g)+ 4 H2(g) = H2O(l)+ C2H5OH (l) 的ΔH
【解】:①×2 + ②×4 - ③ = ④
ΔH=ΔH1×2 +ΔH2×4 -ΔH3
=-283.2×2 -285.8×4 +1370 =-339.2 kJ/mol
【例2】 已知:①H2O(g)===H2O(l) ΔH1=Q1 kJ·mol-1
②C2H5OH(g)===C2H5OH(l) ΔH2=Q2 kJ·mol-1
③C2H5OH(g)+3O2(g)===2CO2(g)+3H2O(g)
ΔH3=Q3 kJ·mol-1
则反应C2H5OH(l)+3O2(g)===2CO2(g)+3H2O(l)的反应热ΔH为( )
A.(Q1+Q2+Q3) kJ·mol-1 B.(3Q1+Q2+Q3) kJ·mol-1
C.(Q1-3Q2+Q3) kJ·mol-1 D.(3Q1-Q2+Q3) kJ·mol-1
【解析】 本题考查对盖斯定律的理解和应用,解答此类问题的常用方法有虚拟途径法和加合法两种,具体求算如下:
(1)设计反应的虚拟过程如下:
则有ΔH=-ΔH2+ΔH3+3ΔH1
=(-Q2+Q3+3Q1) kJ·mol-1。
(2)根据盖斯定律(加合法),令①×3+③-②,
整理得C2H5OH(l)+3O2(g)===2CO2(g)+3H2O(l)
ΔH=3ΔH1+ΔH3-ΔH2=(3Q1+Q3-Q2) kJ·mol-1。
【答案】 D
例3:写出石墨变成金刚石的热化学方程式 (25℃,101kPa时)
查燃烧热表知:
①C(石墨,s)+O2(g)= CO2(g) △H1=-393.5kJ/mol
②C(金刚石,s)+O2(g)= CO2(g) △H2=-395.0kJ/mol
解:①- ②得:
C(石墨,s)= C(金刚石,s) ; △H=+1.5kJ/mol
练习1:已知下列各反应的焓变
①Ca(s)+C(s,石墨)+3/2O2(g)=CaCO3(s) △H1 = -1206.8 kJ/mol
②Ca(s)+1/2O2(g)=CaO(s) △H2= -635.1 kJ/mol
③C(s,石墨)+O2(g)=CO2(g) △H3 = -393.5 kJ/mol
试求④CaCO3(s)=CaO(s)+CO2(g)的焓变
△H4=+178.2kJ/mol
④=②+③-①
练习2:按照盖斯定律,结合下述反应方程式回答问题,已知:
①NH3(g)+HCl(g)=NH4Cl(s) △H1=-176kJ/mol
②NH3(g)+H2O(l)=NH3(aq) △H2=-35.1kJ/mol
③HCl(g) +H2O(l)=HCl(aq) △H3=-72.3kJ/mol
④NH3(aq)+ HCl(aq)=NH4Cl(aq) △H4=-52.3kJ/mol
⑤NH4Cl(s)+2H2O(l)= NH4Cl(aq) △H5=?
则第⑤个方程式中的反应热△H是________。
根据盖斯定律和上述反应方程式得:
⑤=④+③+②-①,
即△H5 = +16.3kJ/mol
“三步”确定热化学方程式或ΔH
找出
调整
加和
根据待求解的热化学方程式中的反应物和生成物找出可用的已知热化学方程式。
①根据待求解的热化学方程式调整可用热化学方程式的方向,同时调整△H的符号。
②根据待求解的热化学方程式将调整好的热化学方程式进行缩小或扩大相应的倍数,同时调整△H的值。
将调整好的热化学方程式和△H分别进行求△H加和。确定目标反应的焓变△H。
1.判断正误(正确的打“√”,错误的打“×”)(1)一个反应一步完成或分几步完成,两者相比,经过的步骤越多,放出的热量越多。 ( )(2)化学反应的反应热与化学反应的始态有关,与终态无关。
( )(3)同一反应的反应热ΔH与化学计量数成正比。 ( )
(3)利用盖斯定律,可计算某些反应的反应热。 ( )
(4)任何化学反应的反应热都可以直接测定。 ( )
×
×
√
√
×
2.下列说法不正确的是( )
①在热化学方程式中无论是反应物还是生成物都必须标明状态 ②所有的化学反应都伴随着能量变化 ③放热反应发生时不必加热 ④吸热反应在加热后才能发生 ⑤化学反应的热效应数值只与参加反应的物质的多少有关 ⑥一般来说,吸热反应在一定条件下也能发生 ⑦根据盖斯定律,反应焓变的大小与反应的途径有关,无论是一步完成还是分几步完成,其总的热效应完全相同
A.②③⑥⑦ B.③④⑤⑦ C.④⑤⑦ D.①③④⑦
B
【解析】放热反应有时需要加热才能实现,如燃烧反应,③错误;有些吸热反应不需要加热就能发生,如铵盐与Ba(OH)2混合研磨就能反应,④错误;化学反应的热效应不仅与反应物的多少有关,还与物质的状态有关,⑤错误;从盖斯定律来看,反应焓变的大小与途径无关,故⑦错误。
3.能源问题是人类社会面临的重大课题,H2、CO、CH3OH都是重要的能源物质,它们的燃烧热依次为285.8 kJ·mol-1、282.5 kJ·mol-1、726.7 kJ·mol-1。已知CO和H2在一定条件下可以合成甲醇CO(g)+2H2(g)===CH3OH(l)。则CO与H2反应合成甲醇的热化学方程式为( )
A.CO(g)+2H2(g)===CH3OH(l) ΔH=-127.4 kJ·mol-1
B.CO(g)+2H2(g)===CH3OH(l) ΔH=+127.4 kJ·mol-1
C.CO(g)+2H2(g)===CH3OH(g) ΔH=-127.4 kJ·mol-1
D.CO(g)+2H2(g)===CH3OH(g) ΔH=+127.4 kJ·mol-1
【解析】 根据题给三种物质的燃烧热可以写出:
H2(g)+1/2O2(g)===H2O(l) ΔH1=-285.8 kJ·mol-1①
CO(g)+1/2O2(g)===CO2(g) ΔH2=-282.5 kJ·mol-1②
CH3OH(l)+3/2O2(g)===CO2(g)+2H2O(l) ΔH3=-726.7 kJ·mol-1③
运用盖斯定律进行计算,即①×2+②-③可得:
CO(g)+2H2(g)===CH3OH(l) ΔH=2ΔH1+ΔH2-ΔH3
=2×(-285.8 kJ·mol-1)+(-282.5 kJ·mol-1)-(-726.7 kJ·mol-1)=-127.4 kJ·mol-1。
A
4.化学反应N2(g)+3H2(g)===2NH3(l)的能量变化如图所示,该反应的ΔH等于( )
A.+2(a-b-c) kJ·mol-1 B.+2(b-a) kJ·mol-1
C.+(b+c-a) kJ·mol-1 D.+(a+b) kJ·mol-1
【解析】 由题图知N2(g)+H2(g)===NH3(l)
需放出(b+c-a)kJ的热量,
故N2(g)+3H2(g)===2NH3(l) ΔH=-2(b+c-a) kJ·mol-1 =2(a-b-c) kJ·mol-1 ,A项正确。
A
小 结
一、盖斯定律
1、定义:
不管化学反应是一步完成或分几步完成,其反应热是相同。
2、特点:
反应的热效应只与始终态有关,与反应途径无关。
正、逆反应的反应热数值相等,符号相反。
3、影响反应热的因素:
温度、压强,物质状态,反应物用量等。
4、应用:
间接计算难以直接测定的反应热。
关键:
目标方程式的“四则运算式”的导出。
方法:
写出目标方程式确定“过渡物质” (要消去的物质)然后用消元法逐一消去“过渡物质”,导出“四则运算式”。
途径:
①虚拟路径法; ②加合法。
