人教版数学九年级上册24.1.3 弧、弦、圆心角 说课课件(共35张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1.3 弧、弦、圆心角 说课课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 548.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-31 12:22:59 | ||
图片预览









文档简介
(共35张PPT)
弧、弦、圆心角说课
1.教材的地位和作用
2. 教学重、难点
教材分析
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
本节教学内容是人教版九年级(上)第二十四章第一节圆的第三课时。本节内容是前面圆的性质的重要体现,是圆的中心对称性的具体化,也是论证同圆或等圆中线段相等、角相等、弧相等的主要依据,同时也是为进行圆的计算提供了方法和依据,所以它在教材中处于重要的位置。
1.教材的地位和作用
教材分析
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教学重点: 圆心角、弧、弦之间关系定理
2.教学重难点
教学难点:“圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明
教材分析
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教材分析
教 学 目 标
教学知识点
1.圆的旋转不变性.
2. 圆心角的概念
3.圆心角、弧、弦之间相等关系定理.
能力训练要求:
1.通过观察、比较、操作、推理、归纳等活动,发展空间观念、推理能力以及概括问题的能力.
2.了解圆心角的概念,学会辨别圆心角。
3.利用圆的旋转不变性,研究圆心角、弧、弦之间相等关系定理
情感与价值观要求:
培养学生积极探索数学问题的态度及方法,渗透旋转变换的思想及由特殊到一般的认识规律。
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教材分析
教法分析
我在本课中借助直观的多媒体教学手段,采取了引导发现法和直观演示法
学法分析
目标分析
教法分析
学法分析
教学设计
板书设计
本节课的教学,引导学生自己动手、动脑,学会观察、归纳,分析、讨论、得出结论。鼓励他们自主探索、合作交流,发扬集体主义精神,从而顺利完成教学目标
教材分析
评价设计
目标分析
教法分析
学法分析
教学设计
活动一:创设情境
活动三:探究定理
活动四:应用新知
活动五:巩固练习
活动六:总结反思
活动二:探索新知
板书设计
教材分析
活动七:布置作业
评价设计
创设情境
(2) ⊙O绕圆心O旋转180度后,你发现了什么?
实物演示:
(1)平行四边形绕对角线交点O旋转180度后,你发现了什么?
(3)平行四边形绕对角线交点O任意旋转一个角度
后,你发现了什么?把⊙O绕圆心O旋转任意一个
角度后,你发现了什么?
设计意图:让学生在实际操作中发现圆的旋转不变性
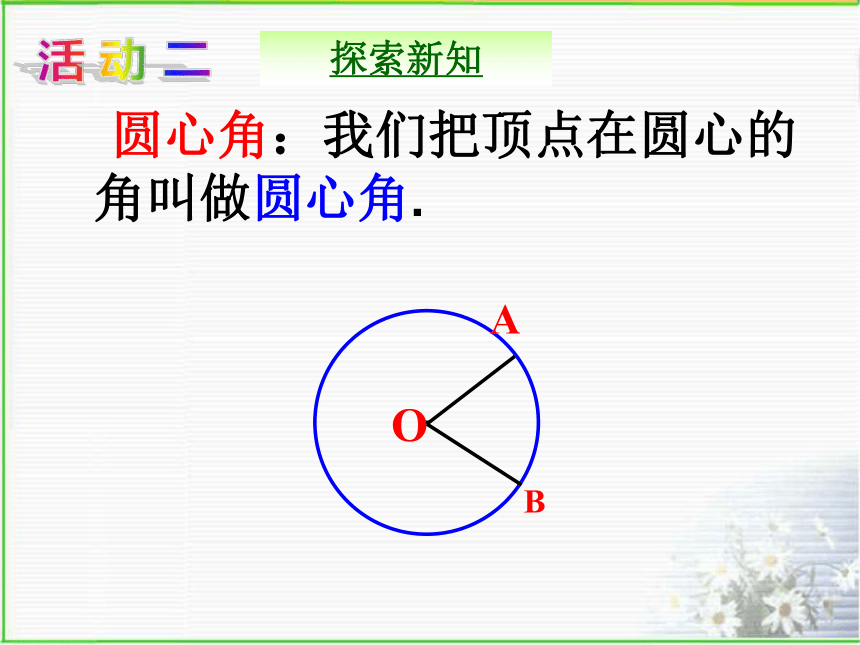
圆心角:我们把顶点在圆心的角叫做圆心角.
·
O
B
A
探索新知
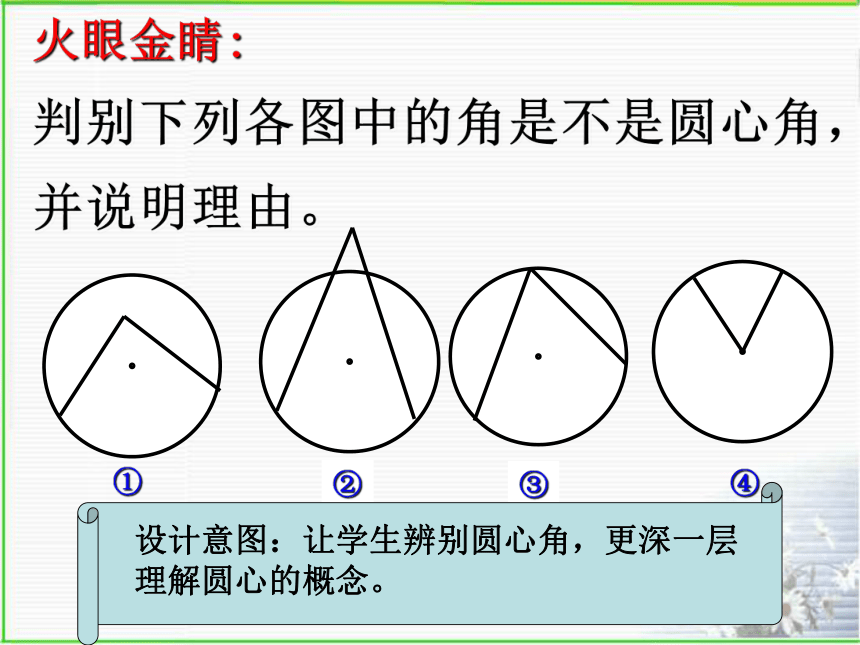
火眼金睛:
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
设计意图:让学生辨别圆心角,更深一层理解圆心的概念。
A
B
C
D
o
下面我们一起来观察一下:在⊙O中有哪些圆心角?
(并说出圆心
角所对的弧,
弦。)
如果: ∠AOB=∠ COD
探究定理
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
∵OA=OC =OB=OD,
∠AOB=∠COD,
当点A与点C重合时,
点B与点D也重合
∴ AB=CD, AB=CD
⌒
⌒
设计意图:通过多媒体动态演示及动手操作,让学生更直观地体会定理。突破重难点。
在同圆或等圆中,相等的弧所对的
圆心角____, 所对的弦____;
在同圆或等圆中,相等的弦所对的
圆心角___,所对的弧____.
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
同圆或等圆中,
两个圆心角、两
条弧、两条弦中
有一组量相等,
它们所对应的其
余各组量也相
等.
定理
如图,因为
,
AB=CD吗?
弧AB与弧CD呢?
O
A
B
C
D
∠AOB=∠COD
设计意图:通过举反例强化对定理的理解突破难点
1. 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___,____.
(2)如果AB=CD ,那么___,______.
(3)如果∠AOB=∠COD,那么_______,______.
·
C
B
A
D
O
⌒ ⌒
应用新知
变式一:在∠AOB= ∠COD的前提下,若将∠AOB和∠COD旋转一定的角度如图所示那么你可以得到哪些结论?
若改变条件如图A,B,C,D是⊙O上的点,∠1=∠2。那么AB还与CD相等吗?
D
B
A
C
1
2
O
·
A
B
C
O
变式二:若AB=CD,将∠AOB和∠COD旋转如图所示使A与D重合,连接BC,且∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
设计意图:变换条件和结论,让学生多角度探索问题,有利于加深学生对定理的应用和对知识内在联系的更深刻的认识。旋转贯穿始终有利于突破难点体现重点。
请同学进一步的思考和想象,你是否可以适当改变条件或旋转图形的方法来给同学出个题互相考验一下?
各显其能
备用题. 将∠AOB和∠COD旋转如图所示且AC、DB是⊙O的两条直径,E是⊙O上一点,AD=EB。求证:BE=CB
⌒
⌒
O
E
C
A
D
B
设计意图:防止学生的不确定性,由此题作为补充。
1.AB为⊙O的直径,AC为弦,
半径OD∥AC
求证:D为BC中点
⌒
C
A
D
B
O
巩固练习
2.如图,以 的顶点A为圆心,AB为半径作 ,分别交BD、AC与E、F两点,交BA的延长线与G.判断 和 是否相等,并说明理由.
B
A
G
F
D
C
E
3. 如图,AB、CD是⊙O的两条弦.
如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
设计意图:对定理进一步的加深理解。
能说出你这节课的收获和体验让大家与你分享吗?
总结反思
分层作业
一、 习题24.1 第2、3题(必做)
二、习题24.1 第10、12题(选做)
布置作业
设计意图:面对学生个体差异,加深对定理的理解
三、为建设我们美丽的校园,学校准备把圆形花坛的外沿分成相等的三部分,每部分用不同颜色的花砖砌成,请你用所学知识帮助设计一种施工方案.
目标分析
教法分析
学法分析
教学设计
板书设计
评价设计
教材分析
§24.1.3 弧、弦、圆心角
一、圆的旋转不变性
二、弧、弦、圆心角
关系定理 学生板演区
三、圆中圆心角、弧、弦
之间的关系定理应用
及其变式
设计意图:体现学生为主体、教师为主导的新课改理念
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教材分析
为了给学生营造一个民主、平等而又富有诗意的课堂,我以新数学课程标准下的基本理念和总体目标为指导思想在教学过程中始终面向全体学生,依据学生的实际水平,选择适当的教学起点和教学方法,充分让学生参与教学,在合作交流的过程中,获得良好的情感体验。通过“实验--观察--猜想--证明”的思想,让每个学生都有所得,我注意前后知识的链接,例题的变式,为学生提供了广阔的思考空间,在学习中感悟生活中的数学美。
弧、弦、圆心角说课
1.教材的地位和作用
2. 教学重、难点
教材分析
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
本节教学内容是人教版九年级(上)第二十四章第一节圆的第三课时。本节内容是前面圆的性质的重要体现,是圆的中心对称性的具体化,也是论证同圆或等圆中线段相等、角相等、弧相等的主要依据,同时也是为进行圆的计算提供了方法和依据,所以它在教材中处于重要的位置。
1.教材的地位和作用
教材分析
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教学重点: 圆心角、弧、弦之间关系定理
2.教学重难点
教学难点:“圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明
教材分析
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教材分析
教 学 目 标
教学知识点
1.圆的旋转不变性.
2. 圆心角的概念
3.圆心角、弧、弦之间相等关系定理.
能力训练要求:
1.通过观察、比较、操作、推理、归纳等活动,发展空间观念、推理能力以及概括问题的能力.
2.了解圆心角的概念,学会辨别圆心角。
3.利用圆的旋转不变性,研究圆心角、弧、弦之间相等关系定理
情感与价值观要求:
培养学生积极探索数学问题的态度及方法,渗透旋转变换的思想及由特殊到一般的认识规律。
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教材分析
教法分析
我在本课中借助直观的多媒体教学手段,采取了引导发现法和直观演示法
学法分析
目标分析
教法分析
学法分析
教学设计
板书设计
本节课的教学,引导学生自己动手、动脑,学会观察、归纳,分析、讨论、得出结论。鼓励他们自主探索、合作交流,发扬集体主义精神,从而顺利完成教学目标
教材分析
评价设计
目标分析
教法分析
学法分析
教学设计
活动一:创设情境
活动三:探究定理
活动四:应用新知
活动五:巩固练习
活动六:总结反思
活动二:探索新知
板书设计
教材分析
活动七:布置作业
评价设计
创设情境
(2) ⊙O绕圆心O旋转180度后,你发现了什么?
实物演示:
(1)平行四边形绕对角线交点O旋转180度后,你发现了什么?
(3)平行四边形绕对角线交点O任意旋转一个角度
后,你发现了什么?把⊙O绕圆心O旋转任意一个
角度后,你发现了什么?
设计意图:让学生在实际操作中发现圆的旋转不变性
圆心角:我们把顶点在圆心的角叫做圆心角.
·
O
B
A
探索新知
火眼金睛:
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
设计意图:让学生辨别圆心角,更深一层理解圆心的概念。
A
B
C
D
o
下面我们一起来观察一下:在⊙O中有哪些圆心角?
(并说出圆心
角所对的弧,
弦。)
如果: ∠AOB=∠ COD
探究定理
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
A
B
C
D
o
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?
如图: ∠AOB=∠ COD
A
B
C
D
o
∵OA=OC =OB=OD,
∠AOB=∠COD,
当点A与点C重合时,
点B与点D也重合
∴ AB=CD, AB=CD
⌒
⌒
设计意图:通过多媒体动态演示及动手操作,让学生更直观地体会定理。突破重难点。
在同圆或等圆中,相等的弧所对的
圆心角____, 所对的弦____;
在同圆或等圆中,相等的弦所对的
圆心角___,所对的弧____.
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
同圆或等圆中,
两个圆心角、两
条弧、两条弦中
有一组量相等,
它们所对应的其
余各组量也相
等.
定理
如图,因为
,
AB=CD吗?
弧AB与弧CD呢?
O
A
B
C
D
∠AOB=∠COD
设计意图:通过举反例强化对定理的理解突破难点
1. 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___,____.
(2)如果AB=CD ,那么___,______.
(3)如果∠AOB=∠COD,那么_______,______.
·
C
B
A
D
O
⌒ ⌒
应用新知
变式一:在∠AOB= ∠COD的前提下,若将∠AOB和∠COD旋转一定的角度如图所示那么你可以得到哪些结论?
若改变条件如图A,B,C,D是⊙O上的点,∠1=∠2。那么AB还与CD相等吗?
D
B
A
C
1
2
O
·
A
B
C
O
变式二:若AB=CD,将∠AOB和∠COD旋转如图所示使A与D重合,连接BC,且∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
设计意图:变换条件和结论,让学生多角度探索问题,有利于加深学生对定理的应用和对知识内在联系的更深刻的认识。旋转贯穿始终有利于突破难点体现重点。
请同学进一步的思考和想象,你是否可以适当改变条件或旋转图形的方法来给同学出个题互相考验一下?
各显其能
备用题. 将∠AOB和∠COD旋转如图所示且AC、DB是⊙O的两条直径,E是⊙O上一点,AD=EB。求证:BE=CB
⌒
⌒
O
E
C
A
D
B
设计意图:防止学生的不确定性,由此题作为补充。
1.AB为⊙O的直径,AC为弦,
半径OD∥AC
求证:D为BC中点
⌒
C
A
D
B
O
巩固练习
2.如图,以 的顶点A为圆心,AB为半径作 ,分别交BD、AC与E、F两点,交BA的延长线与G.判断 和 是否相等,并说明理由.
B
A
G
F
D
C
E
3. 如图,AB、CD是⊙O的两条弦.
如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
设计意图:对定理进一步的加深理解。
能说出你这节课的收获和体验让大家与你分享吗?
总结反思
分层作业
一、 习题24.1 第2、3题(必做)
二、习题24.1 第10、12题(选做)
布置作业
设计意图:面对学生个体差异,加深对定理的理解
三、为建设我们美丽的校园,学校准备把圆形花坛的外沿分成相等的三部分,每部分用不同颜色的花砖砌成,请你用所学知识帮助设计一种施工方案.
目标分析
教法分析
学法分析
教学设计
板书设计
评价设计
教材分析
§24.1.3 弧、弦、圆心角
一、圆的旋转不变性
二、弧、弦、圆心角
关系定理 学生板演区
三、圆中圆心角、弧、弦
之间的关系定理应用
及其变式
设计意图:体现学生为主体、教师为主导的新课改理念
目标分析
教法分析
学法分析
教学设计
评价设计
板书设计
教材分析
为了给学生营造一个民主、平等而又富有诗意的课堂,我以新数学课程标准下的基本理念和总体目标为指导思想在教学过程中始终面向全体学生,依据学生的实际水平,选择适当的教学起点和教学方法,充分让学生参与教学,在合作交流的过程中,获得良好的情感体验。通过“实验--观察--猜想--证明”的思想,让每个学生都有所得,我注意前后知识的链接,例题的变式,为学生提供了广阔的思考空间,在学习中感悟生活中的数学美。
同课章节目录
