华师版数学八年级上册 13.5逆命题与逆定理第2课时 线段垂直平分线课件(共15张PPT)
文档属性
| 名称 | 华师版数学八年级上册 13.5逆命题与逆定理第2课时 线段垂直平分线课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 647.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-31 15:18:46 | ||
图片预览




文档简介
(共15张PPT)
13.5 逆命题与逆定理
第2课时 线段垂直平分线
学习目标
1. 掌握线段的垂直平分线的定理及其逆定理.
2. 会运用线段垂直平分线的性质定理及逆定理解决有关问题.
复习引入
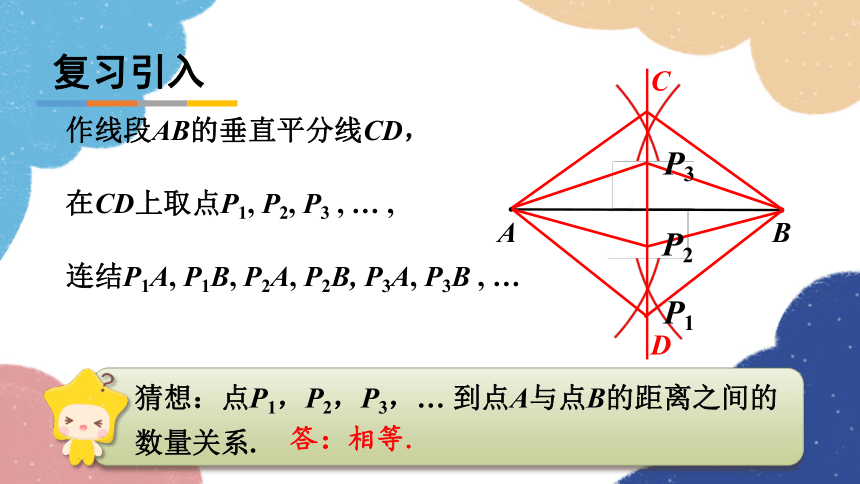
作线段AB的垂直平分线CD,
在CD上取点P1, P2, P3 , … ,
连结P1A, P1B, P2A, P2B, P3A, P3B , …
D
C
A
B
猜想:点P1,P2,P3,… 到点A与点B的距离之间的数量关系.
P1
P2
P3
答:相等.
探究新知
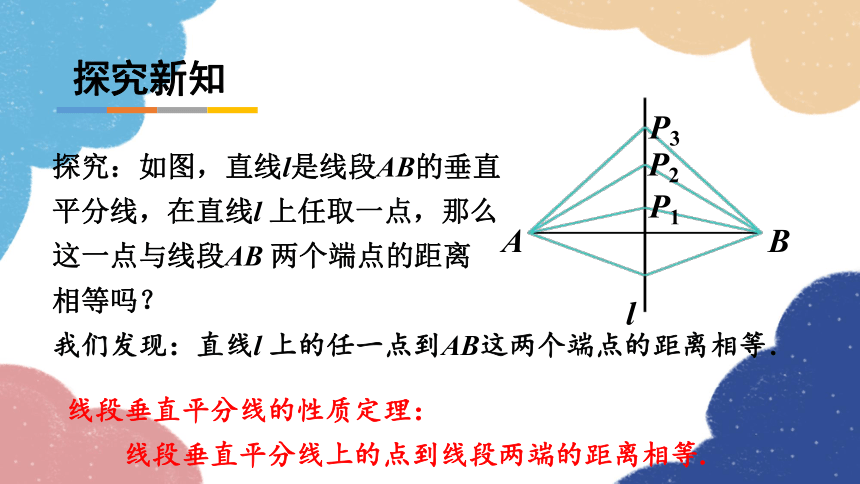
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等.
探究:如图,直线l是线段AB的垂直
平分线,在直线l 上任取一点,那么
这一点与线段AB 两个端点的距离
相等吗?
我们发现:直线l 上的任一点到AB这两个端点的距离相等.
A
B
l
P1
P2
P3
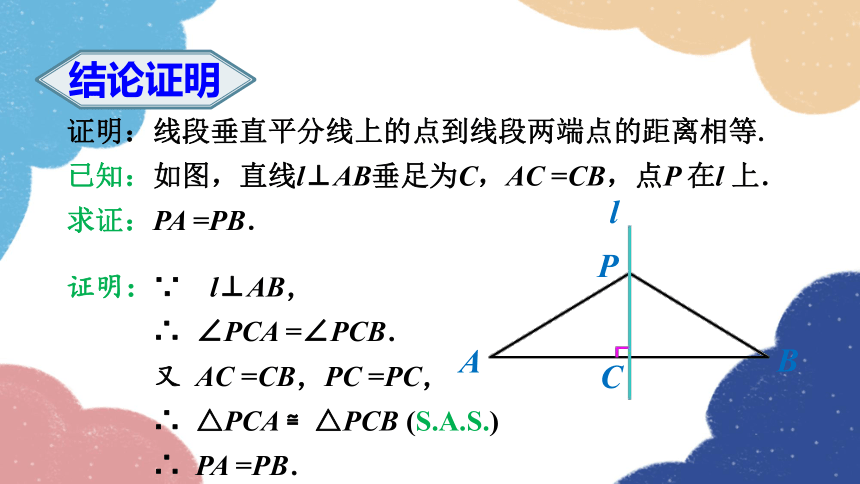
证明:线段垂直平分线上的点到线段两端点的距离相等.
已知:如图,直线l⊥AB垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB (S.A.S.)
∴ PA =PB.
A
B
P
C
l
结论证明
思考:
通过探究已经知道了线段垂直平分线上的点到线段两端点的距离相等. 那么它的逆命题“到线段两端距离相等的点在线段的垂直平分线上”是否为真命题呢?
你能自己证一证这个命题吗?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
证明:如图,过点P 作线段AB 的垂线PC,垂足为C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(H.L.).
∴ AC =BC.又 ∵PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
结论证明
归纳总结
线段垂直平分线的性质定理
①文字语言:线段垂直平分线上的点到线段两端的距离相等.
②几何语言:∵点P 在AB 的垂直平分线上,
∴ PA =PB.
线段垂直平分线性质定理的逆定理
①文字语言:到线段两端距离相等的点在线段的垂直平分线上.
②几何语言:∵PA =PB, ∴点P 在AB 的垂直平分线上.
P
A
B
C
典例精讲
解:∵AD⊥BC,BD =DC,
∴AD 是BC 的垂直平分线,
∴AB =AC.
又∵点C 在AE 的垂直平分线上,
∴AC =CE,∴AB =AC =CE.
又∵BD =DC,∴AB +BD =CD +CE,即AB +BD =DE .
例1 如图, AD⊥BC, BD =DC, 点C在AE的垂直平分线上, AB, AC, CE的长度有什么关系?AB+BD与DE有什么关系?
A
B
C
D
E
例2 在△ABC中,PD,PE分别是AB,AC的垂直平分线,相交于点P,求证:点P也在BC的垂直平分线上.
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
证明:连结PA,PB,PC.
∵ PD,PE分别是AB,AC的垂直平分线,
∴ PA=PB,PA=PC(线段垂直平分线
上的点到线段两端的距离相等).
∴ PB=PC(等量代换),
P
D
E
A
B
C
三角形三边的垂直平分线交于一点,并且这点到三顶点的距离相等.
典例精讲
P
D
E
A
B
C
F
随堂练习
解:∵AB =AC,
∴点A 在BC 的垂直平分线上.
又∵MB =MC,
∴点M 在BC 的垂直平分线上,
∴直线AM 是线段BC 的垂直平分线.
A
B
C
D
M
1. 如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
2. 如图,若AC=12,BC=7,AB的垂直平分线交AB于E,
交AC于D,求△BCD的周长.
D
C
B
E
A
解:∵ED是线段AB的垂直平分线,
∴BD=AD,
又∵ △BCD的周长=BD+DC+BC,
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7
=19.
3. 某区政府为了方便居民的生活,计划在三个住宅小区A、
B、C之间修建一个购物中心.试问:该购物中心应建于
何处,才能使得它到三个小区的距离相等.
A
B
C
分析:作AB、 BC的垂直平分线,交点就是要建的购物中心.
课堂小结
线段垂直平分线上的点到线段两端的距离相等.
到线段两端距离相等的点在线段的垂直平分线上.
互逆定理
线段垂直平分线
13.5 逆命题与逆定理
第2课时 线段垂直平分线
学习目标
1. 掌握线段的垂直平分线的定理及其逆定理.
2. 会运用线段垂直平分线的性质定理及逆定理解决有关问题.
复习引入
作线段AB的垂直平分线CD,
在CD上取点P1, P2, P3 , … ,
连结P1A, P1B, P2A, P2B, P3A, P3B , …
D
C
A
B
猜想:点P1,P2,P3,… 到点A与点B的距离之间的数量关系.
P1
P2
P3
答:相等.
探究新知
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等.
探究:如图,直线l是线段AB的垂直
平分线,在直线l 上任取一点,那么
这一点与线段AB 两个端点的距离
相等吗?
我们发现:直线l 上的任一点到AB这两个端点的距离相等.
A
B
l
P1
P2
P3
证明:线段垂直平分线上的点到线段两端点的距离相等.
已知:如图,直线l⊥AB垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB (S.A.S.)
∴ PA =PB.
A
B
P
C
l
结论证明
思考:
通过探究已经知道了线段垂直平分线上的点到线段两端点的距离相等. 那么它的逆命题“到线段两端距离相等的点在线段的垂直平分线上”是否为真命题呢?
你能自己证一证这个命题吗?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
证明:如图,过点P 作线段AB 的垂线PC,垂足为C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(H.L.).
∴ AC =BC.又 ∵PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
结论证明
归纳总结
线段垂直平分线的性质定理
①文字语言:线段垂直平分线上的点到线段两端的距离相等.
②几何语言:∵点P 在AB 的垂直平分线上,
∴ PA =PB.
线段垂直平分线性质定理的逆定理
①文字语言:到线段两端距离相等的点在线段的垂直平分线上.
②几何语言:∵PA =PB, ∴点P 在AB 的垂直平分线上.
P
A
B
C
典例精讲
解:∵AD⊥BC,BD =DC,
∴AD 是BC 的垂直平分线,
∴AB =AC.
又∵点C 在AE 的垂直平分线上,
∴AC =CE,∴AB =AC =CE.
又∵BD =DC,∴AB +BD =CD +CE,即AB +BD =DE .
例1 如图, AD⊥BC, BD =DC, 点C在AE的垂直平分线上, AB, AC, CE的长度有什么关系?AB+BD与DE有什么关系?
A
B
C
D
E
例2 在△ABC中,PD,PE分别是AB,AC的垂直平分线,相交于点P,求证:点P也在BC的垂直平分线上.
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
证明:连结PA,PB,PC.
∵ PD,PE分别是AB,AC的垂直平分线,
∴ PA=PB,PA=PC(线段垂直平分线
上的点到线段两端的距离相等).
∴ PB=PC(等量代换),
P
D
E
A
B
C
三角形三边的垂直平分线交于一点,并且这点到三顶点的距离相等.
典例精讲
P
D
E
A
B
C
F
随堂练习
解:∵AB =AC,
∴点A 在BC 的垂直平分线上.
又∵MB =MC,
∴点M 在BC 的垂直平分线上,
∴直线AM 是线段BC 的垂直平分线.
A
B
C
D
M
1. 如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
2. 如图,若AC=12,BC=7,AB的垂直平分线交AB于E,
交AC于D,求△BCD的周长.
D
C
B
E
A
解:∵ED是线段AB的垂直平分线,
∴BD=AD,
又∵ △BCD的周长=BD+DC+BC,
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7
=19.
3. 某区政府为了方便居民的生活,计划在三个住宅小区A、
B、C之间修建一个购物中心.试问:该购物中心应建于
何处,才能使得它到三个小区的距离相等.
A
B
C
分析:作AB、 BC的垂直平分线,交点就是要建的购物中心.
课堂小结
线段垂直平分线上的点到线段两端的距离相等.
到线段两端距离相等的点在线段的垂直平分线上.
互逆定理
线段垂直平分线
