江苏省东台中学2024届高三上学期第一次阶段性测试数学试题(PDF版无答案)
文档属性
| 名称 | 江苏省东台中学2024届高三上学期第一次阶段性测试数学试题(PDF版无答案) | 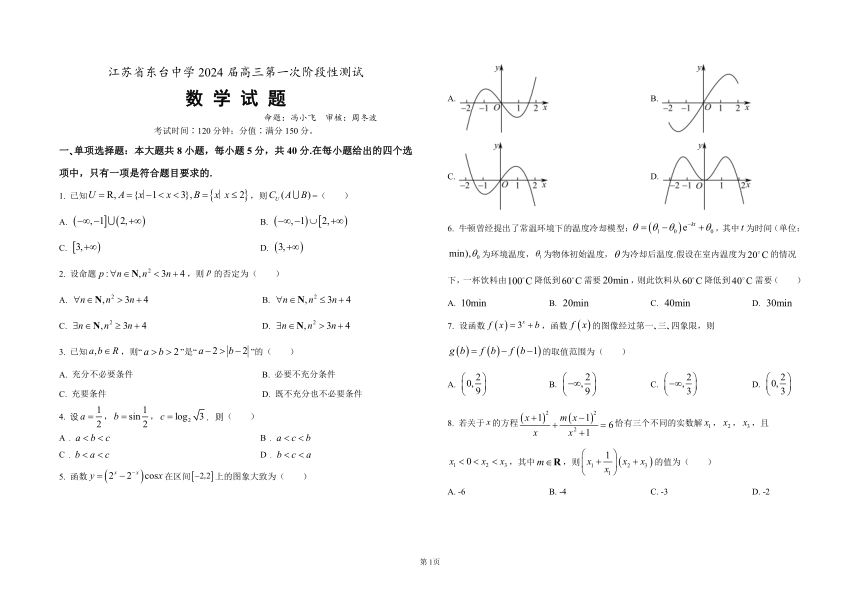 | |
| 格式 | |||
| 文件大小 | 539.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 18:19:40 | ||
图片预览

文档简介
江苏省东台中学 2024届高三第一次阶段性测试
数 学 试 题 A. B.
命题:冯小飞 审核:周冬波
考试时间∶120分钟;分值∶满分 150分。
一 单项选择题:本大题共 8小题,每小题 5分,共 40分.在每小题给出的四个选
项中,只有一项是符合题目要求的. C. D.
1. 已知U R, A {x∣ 1 x 3},B x∣x 2 ,则CU (A B) =( )
A. , 1 2, B. , 1 2,
6. kt牛顿曾经提出了常温环境下的温度冷却模型: 1 0 e 0,其中 t为时间(单位:
C. 3, D. 3, min), 0 为环境温度, 1为物体初始温度, 为冷却后温度.假设在室内温度为 20oC的情况
2. 设命题 p : n N,n2 3n 4,则 p的否定为( )
下,一杯饮料由100 C降低到60 C需要 20min,则此饮料从60 C降低到 40oC需要( )
A. n N,n2 3n 4 B. n N,n2 3n 4 A. 10min B. 20min C. 40min D. 30min
C. n N,n2 3n 4 D. n N,n2 3n 4 7. 设函数 f x 3x b,函数 f x 的图像经过第一 三 四象限,则
3. 已知 a,b R,则“ a b 2 ”是“ a 2 b 2 ”的( ) g b f b f b 1 的取值范围为( )
A. 充分不必要条件 B. 必要不充分条件
A. 0,
2 2 2 2
B. ,
C. , D. 0,
C. 充要条件 D. 既不充分也不必要条件 9 9 3 3
1 1
4. 设 a ,b sin , c log2 3,则
2
( )
2 2 8. x x 1 m x 1
2
若关于 的方程 6恰有三个不同的实数解 x2 1, x2, x3,且
A.a b c B. a c b x x 1
C.b a c D.b c a
x 0 x x x 1
1 2 3 ,其中m R,则 1 x2 x3 的值为( )
5. 函数 y 2x 2 x cosx x1 在区间 2,2 上的图象大致为( )
A. -6 B. -4 C. -3 D. -2
第 1页
{#{QQABAYCAggCAAgBAABgCUQXACkGQkACCAAgGRAAAsAIByANABAA=}#}
二 多选题:本大题共 4小题,每小题 5分,共 20分.在每小题给出的四个选项中, 三 填空题:本大题共 4小题,每小题 5分,共 20分.把答案填在答题卡中的横线.
有多项符合题目要求,全部选对的得 5分,选对但不全的得 2分,有选错的或不 13. 已知函数 y=ax2 +bx+c(a 0) 的图象经过点 ( 1,3)和 (1,1)两点,若 0 c 1,则 a的取值
选的得 0分.
范围是__________.
2sin x cos x
9. 的值可能为( ).
1 cos2 x 1 sin2 x
14. 已知7 3sin 1 7cos .则sin 2 __________.A.0 B.1 C.2 D.3 6
10. 将函数 y 2cos x 1 1图象上的各点的横坐标缩短到原来的 ,纵坐标不变,再向左平移 15. 在中国古代数学著作《九章算术》的“方田”篇中,有一篇关于
2
环形田的面积计算问题:今有环田,中周九十二步,外周一百二十
个单位,得到 f (x)的图象,下列说法正确的是( ).
12 二步,径五步,问为田几何?答:二亩五十五步,其大致意思为:
A. 点 ( ,0)是函数 f (x)图象的对称中心
6 现有一个环形田(如图),中周长 92步,外周长 122步,径长 5步,
5
B. 函数 f (x)在 (0, )上单调递减 问田的面积是多少?答:2亩 55步 2 ,则根据该问题中的相关数据
12
可知该题所取的圆周率 的近似值是______;若已知某环形田的中
C. 函数 f (x) 2 的图象与函数 g(x) 2sin(2x ) 1的图象相同
3
周长 l1步,外周长 l2步,径长 c步,则该环形田的面积为______.(单位:步 2 ).
D. 若 x1, x2是函数的零点,则 x1 x2 是 的整数倍
16. 已知实数 x, y满足 x2 2xy 3y2 4,则 2x2 y2 的最小值是___________.
11. 设函数 y f x 的定义域为R ,且满足 f 1 x f 1 x , f x 2 f x 0,则
四 解答题:本大题共 6小题,共 70分.解答应写出文字说明 证明过程或演算步
下列说法正确的是( )
骤.
A. y f x 1 是偶函数 B. y f x 3 为奇函数
1
17.设全集U R,集合 A x∣ 2x 64
,B x∣y lg x 5 .4
C. f x 是周期为 4的周期函数 D. f 1 0
(1)求 A CUB;
12. 已知 f x x∣x 0 x x 0 (2)设 a为实数,集合C {x | x a} a是定义在 上的奇函数,当 时, .若“ x B ”是“ x C ”的充分条件,求 的取值范围.2 1
x1x2 f x1 f x2 x1 x2 0恒成立,则( )
1
A. y f x 在 ( ,0)上单调递增 B. y f x 在 (0, )上单调递减
2x
C. f 2 1 1 f 3 D. f 2 f 3
6 6
第 2页
{#{QQABAYCAggCAAgBAABgCUQXACkGQkACCAAgGRAAAsAIByANABAA=}#}
x2 2x, (x 0) 21.如图,已知函数 f (x) sin( x )( 0,0 ) ,点 A,B分别是 f (x)的图象与 y
18.已知函数 f (x) 0, (x 0) 是奇函数. 轴、x轴的交点,C,D分别是 f (x)的图象上横坐标为 、 的两点,CD / /x轴,A,B,
x
2 mx, (x 0) 2 3
D共线.
(1)求实数 m的值; (1)求 , 的值;
(2)若函数 f(x)在区间[-1,a-2]上单调递增,求实数 a的取值范围. (2)若关于 x的方程 f (x) k sin 2x [
, 在区间 ]上恰有唯一实根,求实数 k的取值范
12 2
围.
19.已知函数 f x sin x cos x f 1,且 , 0,π .
5
(1)求 f 的值;
1 π(2)若 cos , 0,
,求 cos .3 2
ln 1 x 1 , 2 x 022.已知函数 f x .
ln x , x 0
(1)求函数 f x 的单调递增区间;
20.某服装厂生产一批羽绒服,由于受生产能力和技术水平的限制,会产生一些次品,其次品率 p
1
,0 x m (2)若关于 x的方程 f 2x 1 m有 4个不同的解,记为 x1,x2,x3 ,x4 x1 x2 x 3
x4 ,
x( ) 12 x与日产量 万件 之间满足关系: p (其中m为小于 12的正整数)
3 , x m x 1
4 且
3 x1x2 恒成立,求 的取值范围.x 5
已知每生产 1万件合格的羽绒服可以盈利 3万元,但每生产 1万件次品将亏损 1万元, 4故厂方希
望定出合适的日产量(注:次品率=次品数/生产量,如P=0.1表示每生产 10件产品,有 1件为次品,
其余为合格品).
(1) 试将生产这批羽绒服每天的盈利额 y(万元)表示为日产量 x(万件)的函数;
(2) 当日产量为多少时,可获得最大利润
第 3页
{#{QQABAYCAggCAAgBAABgCUQXACkGQkACCAAgGRAAAsAIByANABAA=}#}
数 学 试 题 A. B.
命题:冯小飞 审核:周冬波
考试时间∶120分钟;分值∶满分 150分。
一 单项选择题:本大题共 8小题,每小题 5分,共 40分.在每小题给出的四个选
项中,只有一项是符合题目要求的. C. D.
1. 已知U R, A {x∣ 1 x 3},B x∣x 2 ,则CU (A B) =( )
A. , 1 2, B. , 1 2,
6. kt牛顿曾经提出了常温环境下的温度冷却模型: 1 0 e 0,其中 t为时间(单位:
C. 3, D. 3, min), 0 为环境温度, 1为物体初始温度, 为冷却后温度.假设在室内温度为 20oC的情况
2. 设命题 p : n N,n2 3n 4,则 p的否定为( )
下,一杯饮料由100 C降低到60 C需要 20min,则此饮料从60 C降低到 40oC需要( )
A. n N,n2 3n 4 B. n N,n2 3n 4 A. 10min B. 20min C. 40min D. 30min
C. n N,n2 3n 4 D. n N,n2 3n 4 7. 设函数 f x 3x b,函数 f x 的图像经过第一 三 四象限,则
3. 已知 a,b R,则“ a b 2 ”是“ a 2 b 2 ”的( ) g b f b f b 1 的取值范围为( )
A. 充分不必要条件 B. 必要不充分条件
A. 0,
2 2 2 2
B. ,
C. , D. 0,
C. 充要条件 D. 既不充分也不必要条件 9 9 3 3
1 1
4. 设 a ,b sin , c log2 3,则
2
( )
2 2 8. x x 1 m x 1
2
若关于 的方程 6恰有三个不同的实数解 x2 1, x2, x3,且
A.a b c B. a c b x x 1
C.b a c D.b c a
x 0 x x x 1
1 2 3 ,其中m R,则 1 x2 x3 的值为( )
5. 函数 y 2x 2 x cosx x1 在区间 2,2 上的图象大致为( )
A. -6 B. -4 C. -3 D. -2
第 1页
{#{QQABAYCAggCAAgBAABgCUQXACkGQkACCAAgGRAAAsAIByANABAA=}#}
二 多选题:本大题共 4小题,每小题 5分,共 20分.在每小题给出的四个选项中, 三 填空题:本大题共 4小题,每小题 5分,共 20分.把答案填在答题卡中的横线.
有多项符合题目要求,全部选对的得 5分,选对但不全的得 2分,有选错的或不 13. 已知函数 y=ax2 +bx+c(a 0) 的图象经过点 ( 1,3)和 (1,1)两点,若 0 c 1,则 a的取值
选的得 0分.
范围是__________.
2sin x cos x
9. 的值可能为( ).
1 cos2 x 1 sin2 x
14. 已知7 3sin 1 7cos .则sin 2 __________.A.0 B.1 C.2 D.3 6
10. 将函数 y 2cos x 1 1图象上的各点的横坐标缩短到原来的 ,纵坐标不变,再向左平移 15. 在中国古代数学著作《九章算术》的“方田”篇中,有一篇关于
2
环形田的面积计算问题:今有环田,中周九十二步,外周一百二十
个单位,得到 f (x)的图象,下列说法正确的是( ).
12 二步,径五步,问为田几何?答:二亩五十五步,其大致意思为:
A. 点 ( ,0)是函数 f (x)图象的对称中心
6 现有一个环形田(如图),中周长 92步,外周长 122步,径长 5步,
5
B. 函数 f (x)在 (0, )上单调递减 问田的面积是多少?答:2亩 55步 2 ,则根据该问题中的相关数据
12
可知该题所取的圆周率 的近似值是______;若已知某环形田的中
C. 函数 f (x) 2 的图象与函数 g(x) 2sin(2x ) 1的图象相同
3
周长 l1步,外周长 l2步,径长 c步,则该环形田的面积为______.(单位:步 2 ).
D. 若 x1, x2是函数的零点,则 x1 x2 是 的整数倍
16. 已知实数 x, y满足 x2 2xy 3y2 4,则 2x2 y2 的最小值是___________.
11. 设函数 y f x 的定义域为R ,且满足 f 1 x f 1 x , f x 2 f x 0,则
四 解答题:本大题共 6小题,共 70分.解答应写出文字说明 证明过程或演算步
下列说法正确的是( )
骤.
A. y f x 1 是偶函数 B. y f x 3 为奇函数
1
17.设全集U R,集合 A x∣ 2x 64
,B x∣y lg x 5 .4
C. f x 是周期为 4的周期函数 D. f 1 0
(1)求 A CUB;
12. 已知 f x x∣x 0 x x 0 (2)设 a为实数,集合C {x | x a} a是定义在 上的奇函数,当 时, .若“ x B ”是“ x C ”的充分条件,求 的取值范围.2 1
x1x2 f x1 f x2 x1 x2 0恒成立,则( )
1
A. y f x 在 ( ,0)上单调递增 B. y f x 在 (0, )上单调递减
2x
C. f 2 1 1 f 3 D. f 2 f 3
6 6
第 2页
{#{QQABAYCAggCAAgBAABgCUQXACkGQkACCAAgGRAAAsAIByANABAA=}#}
x2 2x, (x 0) 21.如图,已知函数 f (x) sin( x )( 0,0 ) ,点 A,B分别是 f (x)的图象与 y
18.已知函数 f (x) 0, (x 0) 是奇函数. 轴、x轴的交点,C,D分别是 f (x)的图象上横坐标为 、 的两点,CD / /x轴,A,B,
x
2 mx, (x 0) 2 3
D共线.
(1)求实数 m的值; (1)求 , 的值;
(2)若函数 f(x)在区间[-1,a-2]上单调递增,求实数 a的取值范围. (2)若关于 x的方程 f (x) k sin 2x [
, 在区间 ]上恰有唯一实根,求实数 k的取值范
12 2
围.
19.已知函数 f x sin x cos x f 1,且 , 0,π .
5
(1)求 f 的值;
1 π(2)若 cos , 0,
,求 cos .3 2
ln 1 x 1 , 2 x 022.已知函数 f x .
ln x , x 0
(1)求函数 f x 的单调递增区间;
20.某服装厂生产一批羽绒服,由于受生产能力和技术水平的限制,会产生一些次品,其次品率 p
1
,0 x m (2)若关于 x的方程 f 2x 1 m有 4个不同的解,记为 x1,x2,x3 ,x4 x1 x2 x 3
x4 ,
x( ) 12 x与日产量 万件 之间满足关系: p (其中m为小于 12的正整数)
3 , x m x 1
4 且
3 x1x2 恒成立,求 的取值范围.x 5
已知每生产 1万件合格的羽绒服可以盈利 3万元,但每生产 1万件次品将亏损 1万元, 4故厂方希
望定出合适的日产量(注:次品率=次品数/生产量,如P=0.1表示每生产 10件产品,有 1件为次品,
其余为合格品).
(1) 试将生产这批羽绒服每天的盈利额 y(万元)表示为日产量 x(万件)的函数;
(2) 当日产量为多少时,可获得最大利润
第 3页
{#{QQABAYCAggCAAgBAABgCUQXACkGQkACCAAgGRAAAsAIByANABAA=}#}
同课章节目录
