1.3.1函数的单调性与最大(小)值第二课时(安徽省巢湖地区巢湖市)
文档属性
| 名称 | 1.3.1函数的单调性与最大(小)值第二课时(安徽省巢湖地区巢湖市) | 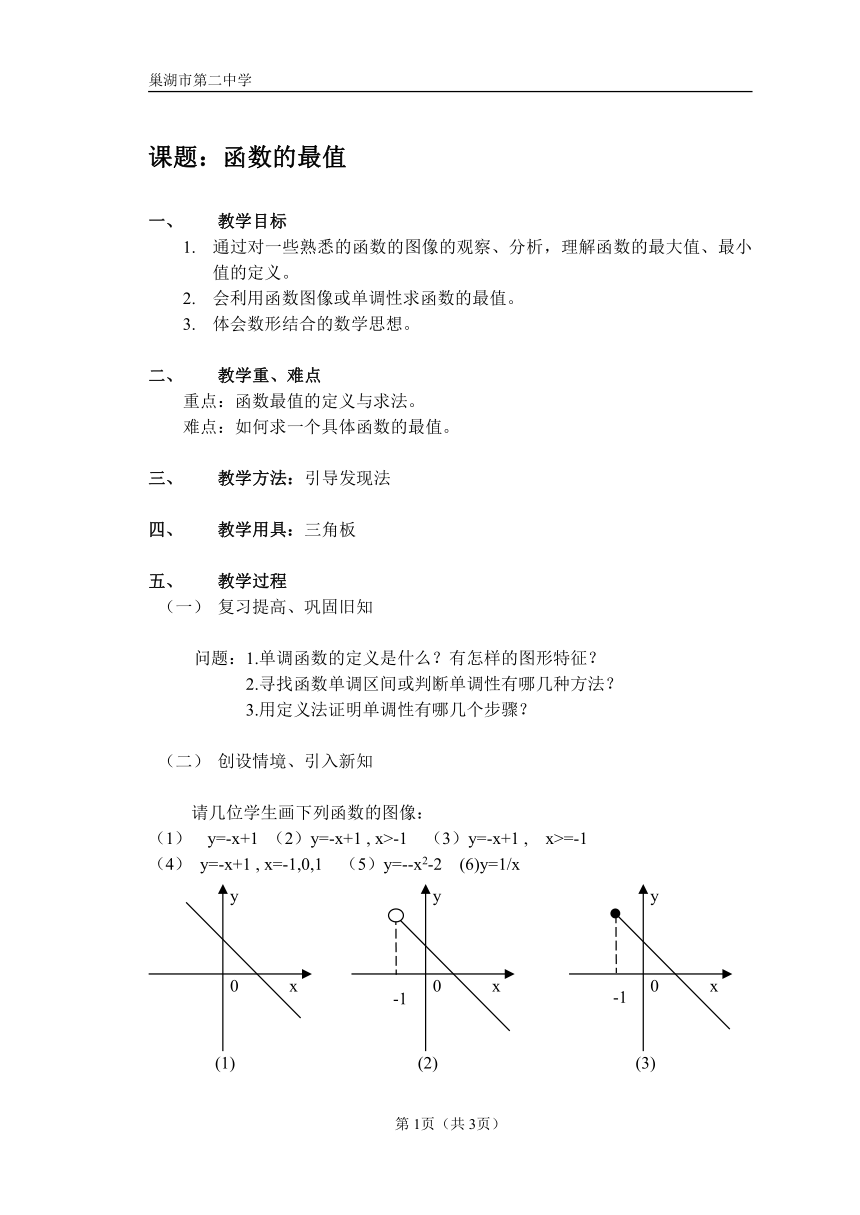 | |
| 格式 | rar | ||
| 文件大小 | 15.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-12 15:01:00 | ||
图片预览

文档简介
巢湖市第二中学
课题:函数的最值
1、 教学目标
1. 通过对一些熟悉的函数的图像的观察、分析,理解函数的最大值、最小值的定义。
2. 会利用函数图像或单调性求函数的最值。
3. 体会数形结合的数学思想。
2、 教学重、难点
重点:函数最值的定义与求法。
难点:如何求一个具体函数的最值。
3、 教学方法:引导发现法
4、 教学用具:三角板
5、 教学过程
(1) 复习提高、巩固旧知
问题:1.单调函数的定义是什么?有怎样的图形特征?
2.寻找函数单调区间或判断单调性有哪几种方法?
3.用定义法证明单调性有哪几个步骤?
(2) 创设情境、引入新知
请几位学生画下列函数的图像:
(1) y=-x+1 (2)y=-x+1 , x>-1 (3)y=-x+1 , x>=-1
(4) y=-x+1 , x=-1,0,1 (5)y=--x2-2 (6)y=1/x
观察以上图像,哪些函数有最大值?由此你能归纳出最大值的定义吗?
(学生观察、比较,用自己的语言描述最大值的定义)
(三)新课学习
1.最大值、最小值的定义
最大值:设函数y=f(x)定义域为I,如果存在实数M满足:
(1) 对于I中任意的x,都有f (x)<=M;
(2) I中存在一个数x0使得f(x0)=M。
则称M是函数y=f(x)的最大值,记作f(x)max=f(x0)=M
最小值:设函数y=f(x)定义域为I,如果存在实数M满足:
(3) 对于I中任意的x,都有f(x)>=M;
(4) I中存在一个数x0使得f(x0)=M。
则称M是函数y=f(x)的最小值,记作f(x)min=f(x0)=M
2.点拨与说明
(1)函数最值的图形特征:函数的最大(小)值是函数图像上最高(低)点的纵坐标。
(2)二次函数y=ax2+bx=c (a不为0)的最值:
①a<0,当x=时,。
②a>0,当x=时,。
(3)若f(x)在[a,b]上为增函数,则f(x)min=f(a), f(x)max=f(b);
若f(x)在[a,b]上为减函数,则f(x)min=f(b), f(x)max=f(a)。
(4) 若f(x)值域为[a,b],则f(x)min=a, f(x)max=b。
3.求函数最值的方法
根据以上的点拨与说明,我们要求函数的最值可以用什么方法?
(1)图像法(2)二次函数法(3)单调性法(4)求值域法
4.反复实践,认识升华
课本例3教学。
对应练习1:(1)函数y=-x2+2x的最大值为 。
(2)函数y=-x2+2x (2=说明:(1)分组讨论,合作交流完成。
(2)思考两题的结果为什么不同。
(3)当二次函数的定义域被限制时,如何求最值。
课本例4教学
说明:利用单调性求最值的解答题,单调性的理由要用定义法书写。
对应练习2:求函数的最大值和最小值。
(请两位成绩较好的学生板演,其他学生在下面做)
五、课堂小结
1.最值的定义及几何特征。
2.求函数求最值的方法
(1)图像法(2)二次函数法(3)单调性法(4)求值域法
3. 利用单调性求最值的解答题,单调性的理由要用定义法书写。
六、作业:习题1.3 A组 5 B组 1、2
七、板书设计:
课题:函数的最值 三、求函数最值的方法:
一、最值的定义 1.
最大值:…… 2.
最小值:…… 3.
二、点拔与说明 4.
1.
2.
3.
4.
八、教后反思:(待定)
-1
(3)
x
y
0
-1
(2)
x
y
0
(1)
x
y
(6)
x
y
0
0
(5)
x
y
0
(4)
x
y
0
第1页(共3页)
课题:函数的最值
1、 教学目标
1. 通过对一些熟悉的函数的图像的观察、分析,理解函数的最大值、最小值的定义。
2. 会利用函数图像或单调性求函数的最值。
3. 体会数形结合的数学思想。
2、 教学重、难点
重点:函数最值的定义与求法。
难点:如何求一个具体函数的最值。
3、 教学方法:引导发现法
4、 教学用具:三角板
5、 教学过程
(1) 复习提高、巩固旧知
问题:1.单调函数的定义是什么?有怎样的图形特征?
2.寻找函数单调区间或判断单调性有哪几种方法?
3.用定义法证明单调性有哪几个步骤?
(2) 创设情境、引入新知
请几位学生画下列函数的图像:
(1) y=-x+1 (2)y=-x+1 , x>-1 (3)y=-x+1 , x>=-1
(4) y=-x+1 , x=-1,0,1 (5)y=--x2-2 (6)y=1/x
观察以上图像,哪些函数有最大值?由此你能归纳出最大值的定义吗?
(学生观察、比较,用自己的语言描述最大值的定义)
(三)新课学习
1.最大值、最小值的定义
最大值:设函数y=f(x)定义域为I,如果存在实数M满足:
(1) 对于I中任意的x,都有f (x)<=M;
(2) I中存在一个数x0使得f(x0)=M。
则称M是函数y=f(x)的最大值,记作f(x)max=f(x0)=M
最小值:设函数y=f(x)定义域为I,如果存在实数M满足:
(3) 对于I中任意的x,都有f(x)>=M;
(4) I中存在一个数x0使得f(x0)=M。
则称M是函数y=f(x)的最小值,记作f(x)min=f(x0)=M
2.点拨与说明
(1)函数最值的图形特征:函数的最大(小)值是函数图像上最高(低)点的纵坐标。
(2)二次函数y=ax2+bx=c (a不为0)的最值:
①a<0,当x=时,。
②a>0,当x=时,。
(3)若f(x)在[a,b]上为增函数,则f(x)min=f(a), f(x)max=f(b);
若f(x)在[a,b]上为减函数,则f(x)min=f(b), f(x)max=f(a)。
(4) 若f(x)值域为[a,b],则f(x)min=a, f(x)max=b。
3.求函数最值的方法
根据以上的点拨与说明,我们要求函数的最值可以用什么方法?
(1)图像法(2)二次函数法(3)单调性法(4)求值域法
4.反复实践,认识升华
课本例3教学。
对应练习1:(1)函数y=-x2+2x的最大值为 。
(2)函数y=-x2+2x (2=
(2)思考两题的结果为什么不同。
(3)当二次函数的定义域被限制时,如何求最值。
课本例4教学
说明:利用单调性求最值的解答题,单调性的理由要用定义法书写。
对应练习2:求函数的最大值和最小值。
(请两位成绩较好的学生板演,其他学生在下面做)
五、课堂小结
1.最值的定义及几何特征。
2.求函数求最值的方法
(1)图像法(2)二次函数法(3)单调性法(4)求值域法
3. 利用单调性求最值的解答题,单调性的理由要用定义法书写。
六、作业:习题1.3 A组 5 B组 1、2
七、板书设计:
课题:函数的最值 三、求函数最值的方法:
一、最值的定义 1.
最大值:…… 2.
最小值:…… 3.
二、点拔与说明 4.
1.
2.
3.
4.
八、教后反思:(待定)
-1
(3)
x
y
0
-1
(2)
x
y
0
(1)
x
y
(6)
x
y
0
0
(5)
x
y
0
(4)
x
y
0
第1页(共3页)
