安徽省芜湖市沈巷中学2023-2024学年八年级上学期开学考试数学试题(含答案)
文档属性
| 名称 | 安徽省芜湖市沈巷中学2023-2024学年八年级上学期开学考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 739.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-31 20:51:45 | ||
图片预览

文档简介
2023-2024学年芜湖市沈巷中学八年级(上)开学
数学试卷
一、选择题(本大题共10小题,每题4分,共40分)
1.已知点M(3,-2)与点在同一条平行于x轴的直线上,且到y轴的距离等于4,那么点的坐标是()
A.(4,2)或(-4,2) B.(4,-2)或(-4,-2)
C.(4,-2)或(-5,-2) D.(4,-2)或(-1,-2)
2.下列说法:①都是27的立方根;②的算术平方根是;③;④的平方根是;⑤-9是81的算术平方根,其中正确的有()
A.1个 B.2个 C.3个 D.4个
3.定义:对于实数a,符号表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-π]=-4,如果,则x的取值范围是()
A. B. C. D.
4.若关于x的不等式组恰好有3个整数解,且关于y的方程的解是非负数,则符合条件的所有整数m之和是()
A.-6 B.-5 C.-3 D.-2
5.如图,点B、D在线段AC上,,E是AB的中点,F是CD的中点,EF=5,则AB的长为()
A.5 B.6 C.7 D.8
6.三角形的三边长分别为5,8,x,则最长边x的取值范围是()
A. B. C. D.
7.一个多边形截取一个角后,形成另一个多边形的内角和是1620,则原来多边形的边数是()
A.10 B.11 C.12 D.以上都有可能
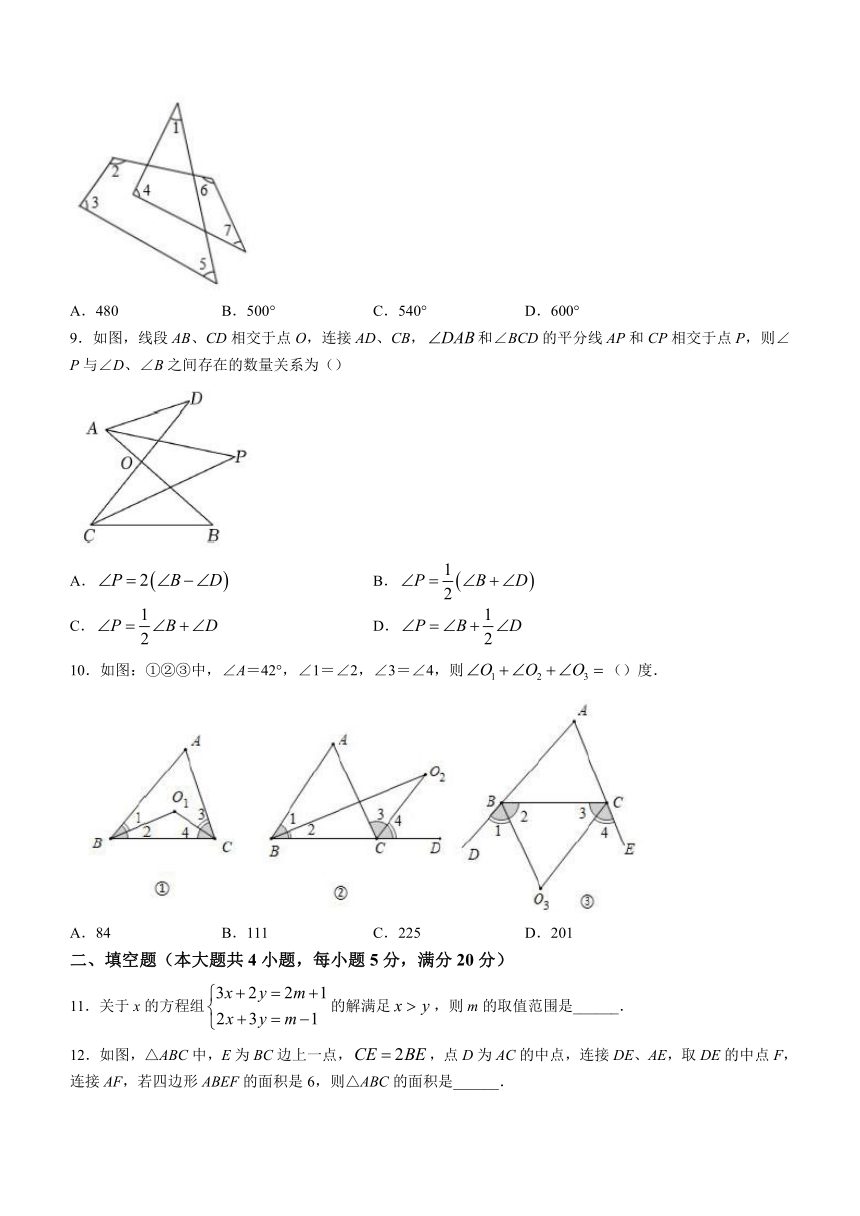
8.如图,()
A.480 B.500° C.540° D.600°
9.如图,线段AB、CD相交于点O,连接AD、CB,和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为()
A. B.
C. D.
10.如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则()度.
A.84 B.111 C.225 D.201
二、填空题(本大题共4小题,每小题5分,满分20分)
11.关于x的方程组的解满足,则m的取值范围是______.
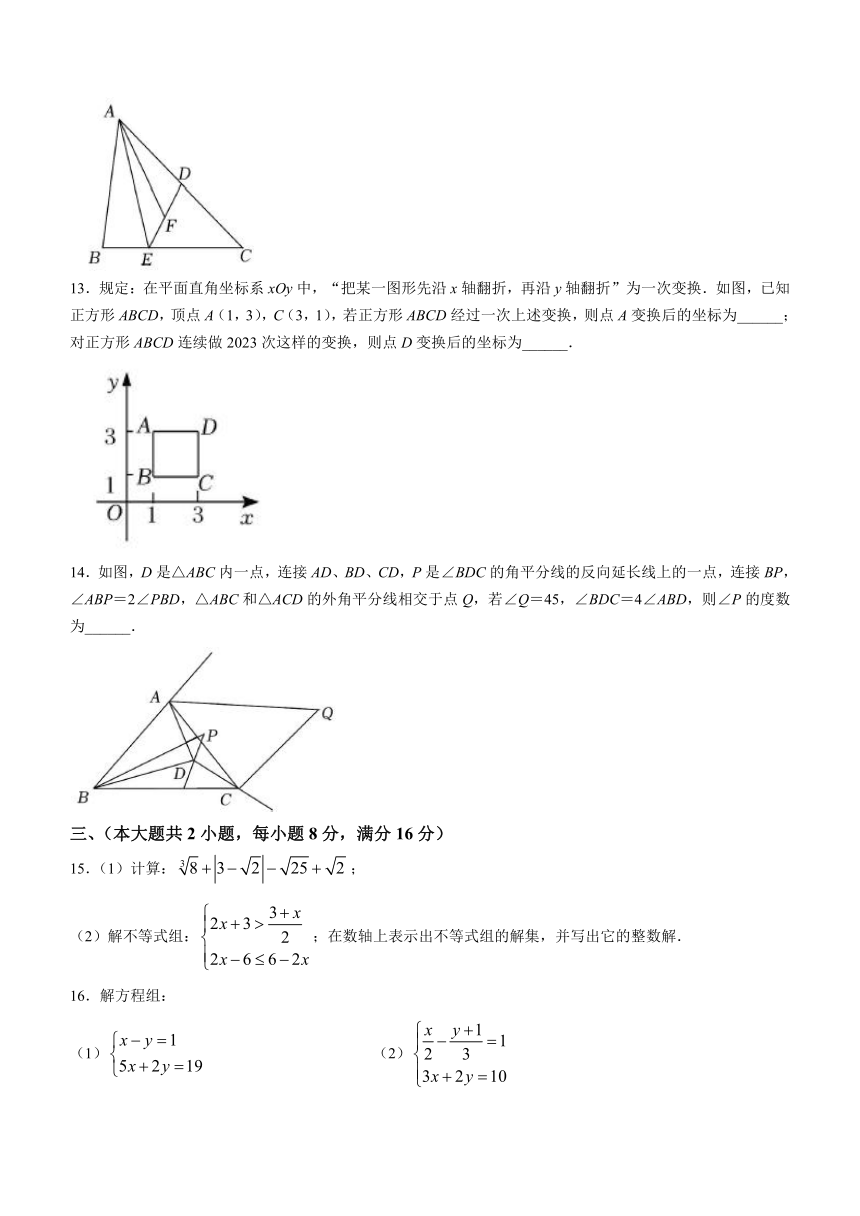
12.如图,△ABC中,E为BC边上一点,,点D为AC的中点,连接DE、AE,取DE的中点F,连接AF,若四边形ABEF的面积是6,则△ABC的面积是______.
13.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变换.如图,已知正方形ABCD,顶点A(1,3),C(3,1),若正方形ABCD经过一次上述变换,则点A变换后的坐标为______;对正方形ABCD连续做2023次这样的变换,则点D变换后的坐标为______.
14.如图,D是△ABC内一点,连接AD、BD、CD,P是∠BDC的角平分线的反向延长线上的一点,连接BP,∠ABP=2∠PBD,△ABC和△ACD的外角平分线相交于点Q,若∠Q=45,∠BDC=4∠ABD,则∠P的度数为______.
三、(本大题共2小题,每小题8分,满分16分)
15.(1)计算:;
(2)解不等式组:;在数轴上表示出不等式组的解集,并写出它的整数解.
16.解方程组:
(1) (2)
四、(本大题共2小题,每小题8分,满分16分)
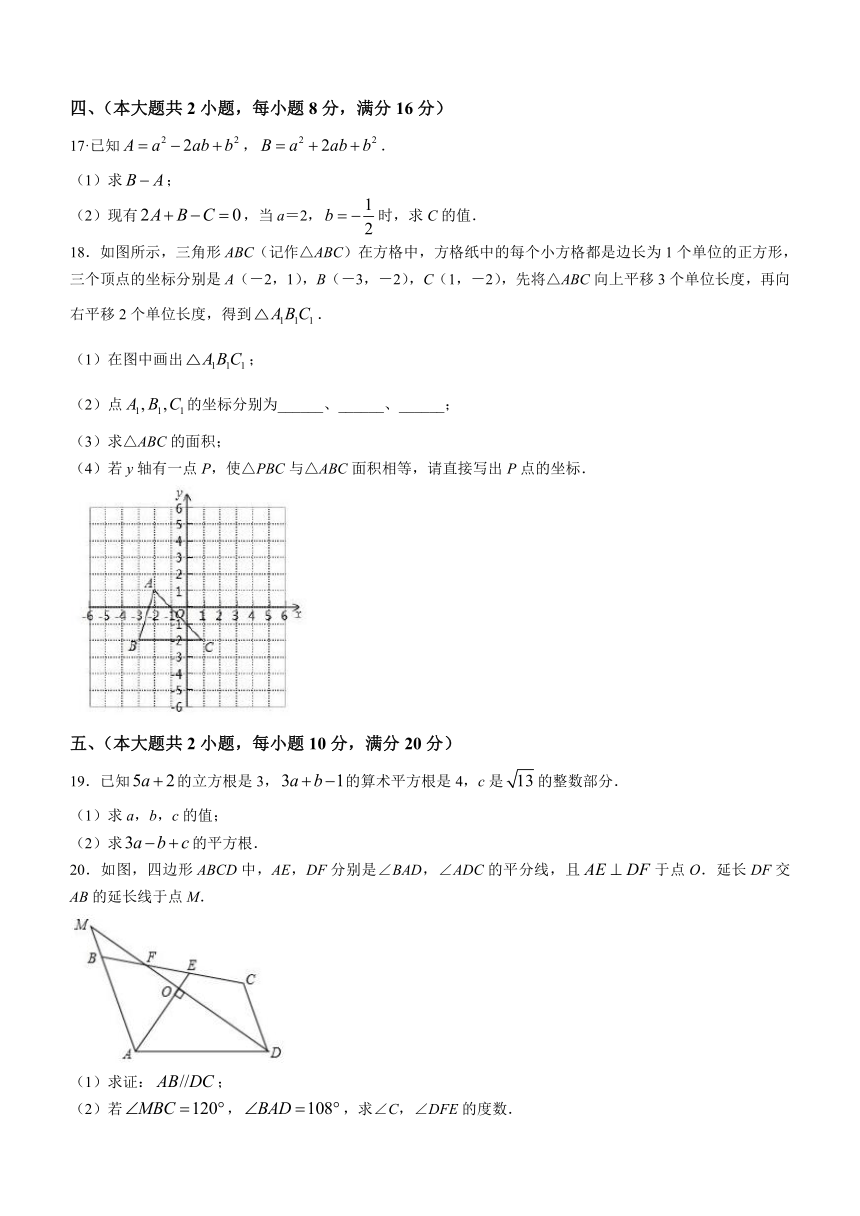
17·已知,.
(1)求;
(2)现有,当a=2,时,求C的值.
18.如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(-2,1),B(-3,-2),C(1,-2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出;
(2)点的坐标分别为______、______、______;
(3)求△ABC的面积;
(4)若y轴有一点P,使△PBC与△ABC面积相等,请直接写出P点的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.已知的立方根是3,的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
20.如图,四边形ABCD中,AE,DF分别是∠BAD,∠ADC的平分线,且于点O.延长DF交AB的延长线于点M.
(1)求证:;
(2)若,,求∠C,∠DFE的度数.
六、(本题满分12分)
21·对于x,y定义一种新运算T,规定:(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:.
(1)已知.
①求a,b的值;
②若关于m的不等式组恰好有三个整数解,求实数k的取值范围.
(2)若对于任意不相等的实数x,y都成立,求a与b满足的关系式.
七、(本题满分12分)
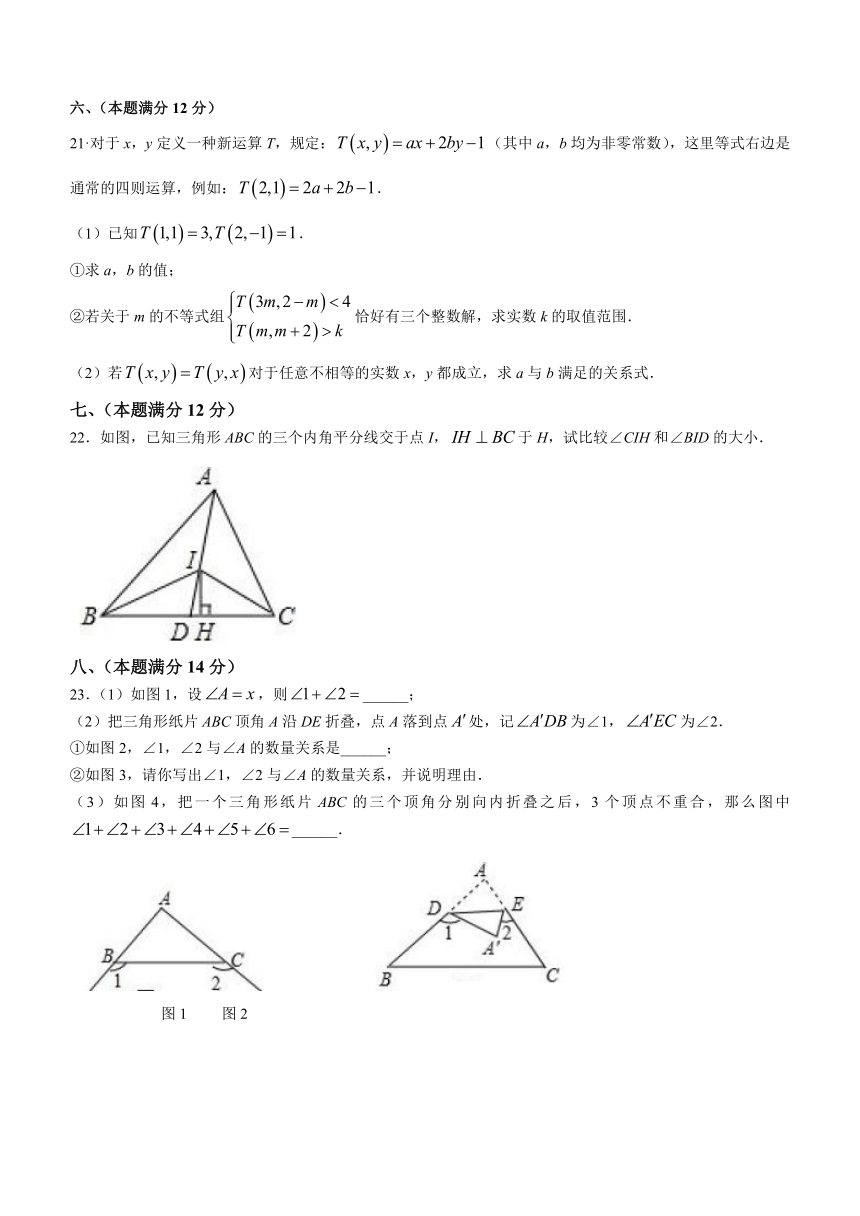
22.如图,已知三角形ABC的三个内角平分线交于点I,于H,试比较∠CIH和∠BID的大小.
八、(本题满分14分)
23.(1)如图1,设,则______;
(2)把三角形纸片ABC顶角A沿DE折叠,点A落到点处,记为∠1,为∠2.
①如图2,∠1,∠2与∠A的数量关系是______;
②如图3,请你写出∠1,∠2与∠A的数量关系,并说明理由.
(3)如图4,把一个三角形纸片ABC的三个顶角分别向内折叠之后,3个顶点不重合,那么图中______.
图1 图2
图3 图4
2023-2024学年芜湖市沈巷中学八年级(上)开学数学试卷
参考答案与评分细则
一、选择题(本大题共10小题,每题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B D D C B D
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 12.12 13.(-3,-3) 14.50
三、(本大题共2小题,每小题8分,满分16分)
15.解:(1)
;
(2),
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:
该不等式组的整数解为:0,1,2,3. 8分
16.解:(1),
,
解得,
把代入①,得,
∴此方程组的解 8分
四、(本大题共2小题,每小题8分,满分16分)
17.解:(1)∵,,
∴
; 4分
(2)∵,
∴
,
当a=2,时,
. 8分
18.解:(1)如图,即为所求作. 2分
(2). 4分
(3) 6分
(4)如图,满足条件的点P的坐标为(0,1)或(0,-5). 8分
五、(本大题共2小题,每小题10分,满分20分)
19.解:(1)∵的立方根是3,的算术平方根是4,
∴,,
∴,,
∵c是的整数部分,
∴. 5分
(2)将a=5,b=2,c=3代入得:,
∴的平方根是. 10分
20·解:(1)证明:∵AE,DF分别是∠BAD,∠ADC的平分线,
∴,,
∵,
∴.
∴,
∴,
∴; 5分
(2)∵
∴.
∵,
∴∠C=120°,
∵∠BAD=108°,
∴∠ADC=72°,
∴
∴. 10分
六.(本题满分12分)
21.解:(1)①根据题意得:,,
解得:a=2,b=1;
②根据题意得:,
由①得:;
由②得:
∴不等式组的解集为,
∵不等式组恰好有3个整数解,即m=0,-1,-2,
∴,
解得; 8分
(2)由,得到,
整理得:,
∵对任意实数x,y都成立.
∴,即. 12分
七、(本题满分12分)
22.解:因为AI、BI、CI为三角形ABC的角平分线,
所以,
. 3分
所以
. 8分
所以.
又因为,,
,
,
所以.
所以和是相等的关系. 12分
八.(本题满分14分)
23.解:(1);
故答案为:; 2分
(2)①如图2,猜想:,理由是:
由折叠得:
∵,
∴,
∴;
故答案为:; 6分
②如图3,,理由是:
∵,
∴,
∵,
∴,
∴; 10分
(3)如图4,由题意知,
又∵,
,
∴
故答案为:. 4分
图4 图3
数学试卷
一、选择题(本大题共10小题,每题4分,共40分)
1.已知点M(3,-2)与点在同一条平行于x轴的直线上,且到y轴的距离等于4,那么点的坐标是()
A.(4,2)或(-4,2) B.(4,-2)或(-4,-2)
C.(4,-2)或(-5,-2) D.(4,-2)或(-1,-2)
2.下列说法:①都是27的立方根;②的算术平方根是;③;④的平方根是;⑤-9是81的算术平方根,其中正确的有()
A.1个 B.2个 C.3个 D.4个
3.定义:对于实数a,符号表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-π]=-4,如果,则x的取值范围是()
A. B. C. D.
4.若关于x的不等式组恰好有3个整数解,且关于y的方程的解是非负数,则符合条件的所有整数m之和是()
A.-6 B.-5 C.-3 D.-2
5.如图,点B、D在线段AC上,,E是AB的中点,F是CD的中点,EF=5,则AB的长为()
A.5 B.6 C.7 D.8
6.三角形的三边长分别为5,8,x,则最长边x的取值范围是()
A. B. C. D.
7.一个多边形截取一个角后,形成另一个多边形的内角和是1620,则原来多边形的边数是()
A.10 B.11 C.12 D.以上都有可能
8.如图,()
A.480 B.500° C.540° D.600°
9.如图,线段AB、CD相交于点O,连接AD、CB,和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为()
A. B.
C. D.
10.如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则()度.
A.84 B.111 C.225 D.201
二、填空题(本大题共4小题,每小题5分,满分20分)
11.关于x的方程组的解满足,则m的取值范围是______.
12.如图,△ABC中,E为BC边上一点,,点D为AC的中点,连接DE、AE,取DE的中点F,连接AF,若四边形ABEF的面积是6,则△ABC的面积是______.
13.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变换.如图,已知正方形ABCD,顶点A(1,3),C(3,1),若正方形ABCD经过一次上述变换,则点A变换后的坐标为______;对正方形ABCD连续做2023次这样的变换,则点D变换后的坐标为______.
14.如图,D是△ABC内一点,连接AD、BD、CD,P是∠BDC的角平分线的反向延长线上的一点,连接BP,∠ABP=2∠PBD,△ABC和△ACD的外角平分线相交于点Q,若∠Q=45,∠BDC=4∠ABD,则∠P的度数为______.
三、(本大题共2小题,每小题8分,满分16分)
15.(1)计算:;
(2)解不等式组:;在数轴上表示出不等式组的解集,并写出它的整数解.
16.解方程组:
(1) (2)
四、(本大题共2小题,每小题8分,满分16分)
17·已知,.
(1)求;
(2)现有,当a=2,时,求C的值.
18.如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(-2,1),B(-3,-2),C(1,-2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出;
(2)点的坐标分别为______、______、______;
(3)求△ABC的面积;
(4)若y轴有一点P,使△PBC与△ABC面积相等,请直接写出P点的坐标.
五、(本大题共2小题,每小题10分,满分20分)
19.已知的立方根是3,的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
20.如图,四边形ABCD中,AE,DF分别是∠BAD,∠ADC的平分线,且于点O.延长DF交AB的延长线于点M.
(1)求证:;
(2)若,,求∠C,∠DFE的度数.
六、(本题满分12分)
21·对于x,y定义一种新运算T,规定:(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:.
(1)已知.
①求a,b的值;
②若关于m的不等式组恰好有三个整数解,求实数k的取值范围.
(2)若对于任意不相等的实数x,y都成立,求a与b满足的关系式.
七、(本题满分12分)
22.如图,已知三角形ABC的三个内角平分线交于点I,于H,试比较∠CIH和∠BID的大小.
八、(本题满分14分)
23.(1)如图1,设,则______;
(2)把三角形纸片ABC顶角A沿DE折叠,点A落到点处,记为∠1,为∠2.
①如图2,∠1,∠2与∠A的数量关系是______;
②如图3,请你写出∠1,∠2与∠A的数量关系,并说明理由.
(3)如图4,把一个三角形纸片ABC的三个顶角分别向内折叠之后,3个顶点不重合,那么图中______.
图1 图2
图3 图4
2023-2024学年芜湖市沈巷中学八年级(上)开学数学试卷
参考答案与评分细则
一、选择题(本大题共10小题,每题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B D D C B D
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 12.12 13.(-3,-3) 14.50
三、(本大题共2小题,每小题8分,满分16分)
15.解:(1)
;
(2),
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:
该不等式组的整数解为:0,1,2,3. 8分
16.解:(1),
,
解得,
把代入①,得,
∴此方程组的解 8分
四、(本大题共2小题,每小题8分,满分16分)
17.解:(1)∵,,
∴
; 4分
(2)∵,
∴
,
当a=2,时,
. 8分
18.解:(1)如图,即为所求作. 2分
(2). 4分
(3) 6分
(4)如图,满足条件的点P的坐标为(0,1)或(0,-5). 8分
五、(本大题共2小题,每小题10分,满分20分)
19.解:(1)∵的立方根是3,的算术平方根是4,
∴,,
∴,,
∵c是的整数部分,
∴. 5分
(2)将a=5,b=2,c=3代入得:,
∴的平方根是. 10分
20·解:(1)证明:∵AE,DF分别是∠BAD,∠ADC的平分线,
∴,,
∵,
∴.
∴,
∴,
∴; 5分
(2)∵
∴.
∵,
∴∠C=120°,
∵∠BAD=108°,
∴∠ADC=72°,
∴
∴. 10分
六.(本题满分12分)
21.解:(1)①根据题意得:,,
解得:a=2,b=1;
②根据题意得:,
由①得:;
由②得:
∴不等式组的解集为,
∵不等式组恰好有3个整数解,即m=0,-1,-2,
∴,
解得; 8分
(2)由,得到,
整理得:,
∵对任意实数x,y都成立.
∴,即. 12分
七、(本题满分12分)
22.解:因为AI、BI、CI为三角形ABC的角平分线,
所以,
. 3分
所以
. 8分
所以.
又因为,,
,
,
所以.
所以和是相等的关系. 12分
八.(本题满分14分)
23.解:(1);
故答案为:; 2分
(2)①如图2,猜想:,理由是:
由折叠得:
∵,
∴,
∴;
故答案为:; 6分
②如图3,,理由是:
∵,
∴,
∵,
∴,
∴; 10分
(3)如图4,由题意知,
又∵,
,
∴
故答案为:. 4分
图4 图3
同课章节目录
