14.2 勾股定理的应用[上学期]
图片预览






文档简介
(共18张PPT)
勾股定理的应用
连云港市海州区新坝中学 张才宝
同学们看过斜拉桥吗?
斜拉桥上可以看到许多直角三角形。
如果知道桥面以上的索塔AB的高,怎么计算各条拉索AC、AD、AE……的长?
如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,如何求梯子的顶端与地面的距离h
我知道了,要解决上面的问题,必须要用
勾股定理
在西方又称毕达哥拉斯定理耶!
直角三角形中,两直角边的平方和等于斜边平方。
C
B
a 勾
股
c 弦
b
勾股定理
用数学式子可表示为:
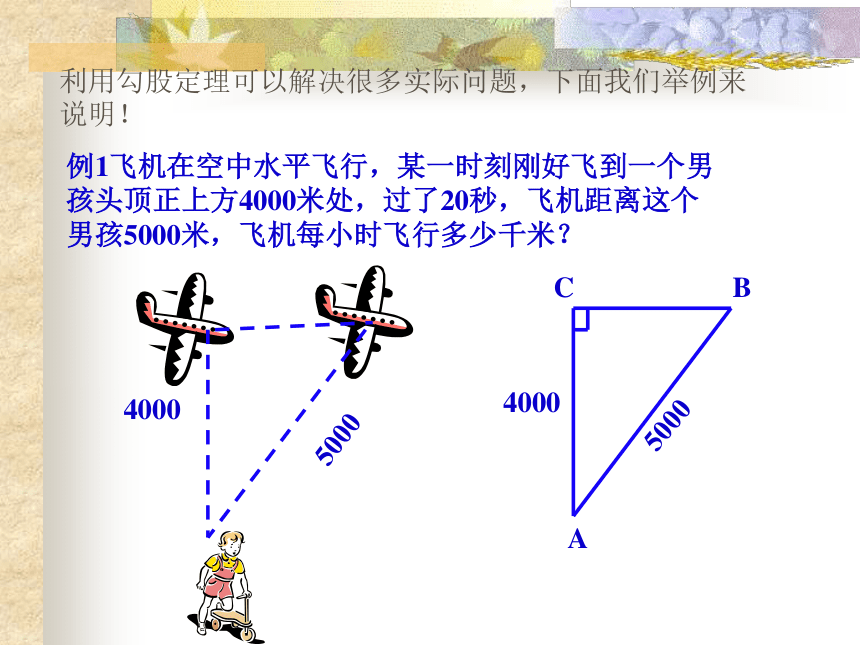
利用勾股定理可以解决很多实际问题,下面我们举例来说明!
5000
4000
C
B
A
5000
4000
例1飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
知识链接
例2从地图上看,南京玄武湖东西向隧道与中央路北段及龙蟠路大致成直角三角形。从B处到C处,如果直接走湖底隧道BC,将比绕道BA(约1.36km),和AC (约2.95km)减少多少行程
(精确到0.1km)
A
B
C
解:在Rt ABC中,由勾股定理得
画板
例4.某农民开垦出一块三边长分别为7m,8m,9m三角形地块准备种植花生,聪明的同学你能帮他算一算这块地的面积吗?
不是直角三角形怎么办呢?
我有办法可以把它转化为直角三角形,问题不就容易了吗?
D
我的具体做法如下:
P83(1),P84(2)
本节课你最大的收获是什么?
再见
勾股定理的应用
连云港市海州区新坝中学 张才宝
同学们看过斜拉桥吗?
斜拉桥上可以看到许多直角三角形。
如果知道桥面以上的索塔AB的高,怎么计算各条拉索AC、AD、AE……的长?
如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,如何求梯子的顶端与地面的距离h
我知道了,要解决上面的问题,必须要用
勾股定理
在西方又称毕达哥拉斯定理耶!
直角三角形中,两直角边的平方和等于斜边平方。
C
B
a 勾
股
c 弦
b
勾股定理
用数学式子可表示为:
利用勾股定理可以解决很多实际问题,下面我们举例来说明!
5000
4000
C
B
A
5000
4000
例1飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
知识链接
例2从地图上看,南京玄武湖东西向隧道与中央路北段及龙蟠路大致成直角三角形。从B处到C处,如果直接走湖底隧道BC,将比绕道BA(约1.36km),和AC (约2.95km)减少多少行程
(精确到0.1km)
A
B
C
解:在Rt ABC中,由勾股定理得
画板
例4.某农民开垦出一块三边长分别为7m,8m,9m三角形地块准备种植花生,聪明的同学你能帮他算一算这块地的面积吗?
不是直角三角形怎么办呢?
我有办法可以把它转化为直角三角形,问题不就容易了吗?
D
我的具体做法如下:
P83(1),P84(2)
本节课你最大的收获是什么?
再见
