数学人教A版(2019)必修第一册1.5.1全称量词与存在量词 课件(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册1.5.1全称量词与存在量词 课件(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 20:20:26 | ||
图片预览






文档简介
(共16张PPT)
1.5 全称量词与存在量词
美国著名作家马克-吐温有一次演说,当谈到国会中某些议员卑鄙龌龊的行径时,情绪激动,不能自已,说道:“美国国会中有些议员不是东西!”事后,某些议员联合起来攻击马克-吐温,要求他赔礼道歉,承认错误,并扬言如不照办,就要向法院控告他的诽谤罪。
马克-吐温于是在报纸上发表了这样一个声明:
“本人上次谈话时说‘美国国会中有些议员是混蛋’,确有不妥之处,而且不符合事实。现郑重声明如下:美国国会中有些议员是东西。――马克-吐温。”
这一来,那些议员无法追究他的诽谤罪了,但却陷入了更尴尬的处境。
下列语句是命题吗?
(1)
(2)2是整数
(3)对所有的,
(4)对任意一个,2是整数
用一个短语对变量的取值范围进行限定,使它们成为一个命题,这样的短语称为量词。
全称量词
还有哪些常见的全称量词?
全称量词 定义 短语“ ”“ ”在逻辑中通常叫做全称量词
符号表示 ___
全称量词命题 定义 含有 量词的命题,叫做全称量词命题
一般形式 对M中 x,p(x)成立
符号表示 ,p(x)
所有的
任意一个
全称
任意一个
x∈M
全称量词与全称量词命题:
阅读课本P27 例1,完成P28练习T1
下列语句是命题吗?
(1)
(2)能被2和3整除
(3)存在一个,使
(4)至少有一个,能被2和3整除
存在量词
还有哪些常见的存在量词?
存在量词与存在量词命题:
存在 量词 定义 短语“ ”“ ”在逻辑中通常叫做存在量词
符号表示 _____
存在量词命题 定义 含有 量词的命题,叫做存在量词命题
一般形式 M中的元素x,p(x)成立
符号表示 ,p(x)
存在一个
至少有一个
存在
存在
x∈M
阅读课本P28 例2,完成P28练习T2
例题1 下列命题是全称量词命题还是存在量词命题,并判断其真假.
(1)任意实数的平方都是正数;
(2)0乘以任何数都等于0;
(3)有的老师既能教中学数学,也能教中学物理;
(4)某些三角形的三内角都小于60°;
(5)任何一个实数都有相反数.
全称量词命题(假)
全称量词命题(真)
存在量词命题
(真)
存在量词命题(假)
全称量词命题(真)
x∈M,p(x)为真:能在集合M中找出一个元素x,使p(x)成立;
x∈M,p(x)为假:在集合M中,使p(x)成立的元素x不存在.
判定一个存在量词命题的真假:
x∈M,p(x)为真:对集合M中每一个元素x,
都有p(x)成立;
x∈M,p(x)为假:在集合M中存在一个元素x,
使得p(x)不成立.
判定一个全称量词命题的真假:
例题2 判断下列命题的真假.
(1) x∈R,x2>x;
(2) x∈Q,x2-8=0;
(3) x∈R,x2+x+1>0;
(4) x∈{x|x是无理数},x2是无理数;
(5) a,b∈R,a2+b2≥2ab
真
假
真
真
真
量词
全称量词
存在量词
全称量词命题
存在量词命题
x∈M,p(x)
x∈M,p(x)
判断命题真假
如何判断全称量词命题与存在量词命题的真假
假命题
真命题
对任意x∈M
都有p(x)成立
存在x∈M
使得p(x)成立
x∈M,p(x)
x∈M,p(x)
存在x∈M使
得p(x)不成立
对任意x∈M
p(x)不成立
课后练习
1.下列命题中,不是全称量词命题的是( )
A.任何一个实数乘0都等于0
B.自然数都是正整数
C.对于任意x∈Z,2x+1是奇数
D.一定存在没有最大值的二次函数
D
2.下列命题中,存在量词命题的个数是( )
①有些自然数是偶数;
②正方形是菱形;
③能被6整除的数也能被3整除;
④对任意实数a,b,c关于x的方程ax2+bx+c=0都有两个实数解.
A.0 B.1
C.2 D.3
课后练习
B
3.下列命题是“ x∈R,x2>3”的另一种表述方法的是( )
A.有一个x∈R,使x2>3成立
B.对有些x∈R,使x2>3成立
C.任选一个x∈R,使x2>3成立
D.至少有一个x∈R,使x2>3成立
课后练习
C
4.对任意x>8,x>a恒成立,则实数a的取值范围是________.
课后练习
答案:a≤8
课后练习
1.5 全称量词与存在量词
美国著名作家马克-吐温有一次演说,当谈到国会中某些议员卑鄙龌龊的行径时,情绪激动,不能自已,说道:“美国国会中有些议员不是东西!”事后,某些议员联合起来攻击马克-吐温,要求他赔礼道歉,承认错误,并扬言如不照办,就要向法院控告他的诽谤罪。
马克-吐温于是在报纸上发表了这样一个声明:
“本人上次谈话时说‘美国国会中有些议员是混蛋’,确有不妥之处,而且不符合事实。现郑重声明如下:美国国会中有些议员是东西。――马克-吐温。”
这一来,那些议员无法追究他的诽谤罪了,但却陷入了更尴尬的处境。
下列语句是命题吗?
(1)
(2)2是整数
(3)对所有的,
(4)对任意一个,2是整数
用一个短语对变量的取值范围进行限定,使它们成为一个命题,这样的短语称为量词。
全称量词
还有哪些常见的全称量词?
全称量词 定义 短语“ ”“ ”在逻辑中通常叫做全称量词
符号表示 ___
全称量词命题 定义 含有 量词的命题,叫做全称量词命题
一般形式 对M中 x,p(x)成立
符号表示 ,p(x)
所有的
任意一个
全称
任意一个
x∈M
全称量词与全称量词命题:
阅读课本P27 例1,完成P28练习T1
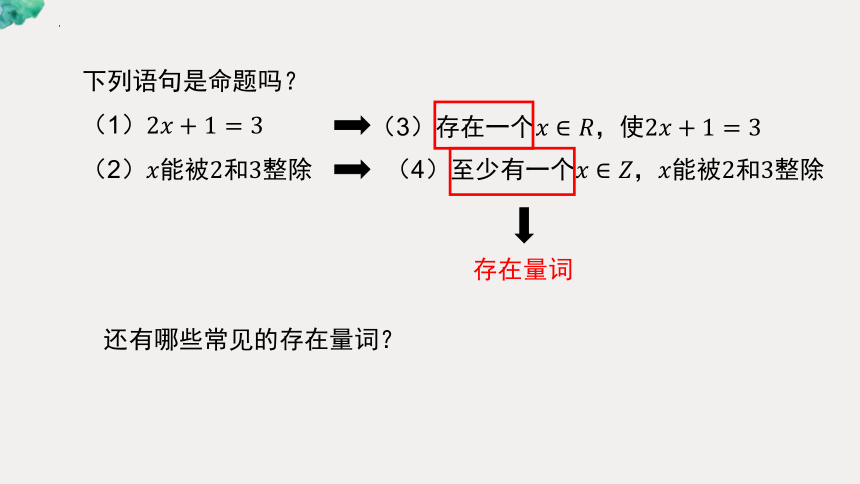
下列语句是命题吗?
(1)
(2)能被2和3整除
(3)存在一个,使
(4)至少有一个,能被2和3整除
存在量词
还有哪些常见的存在量词?
存在量词与存在量词命题:
存在 量词 定义 短语“ ”“ ”在逻辑中通常叫做存在量词
符号表示 _____
存在量词命题 定义 含有 量词的命题,叫做存在量词命题
一般形式 M中的元素x,p(x)成立
符号表示 ,p(x)
存在一个
至少有一个
存在
存在
x∈M
阅读课本P28 例2,完成P28练习T2
例题1 下列命题是全称量词命题还是存在量词命题,并判断其真假.
(1)任意实数的平方都是正数;
(2)0乘以任何数都等于0;
(3)有的老师既能教中学数学,也能教中学物理;
(4)某些三角形的三内角都小于60°;
(5)任何一个实数都有相反数.
全称量词命题(假)
全称量词命题(真)
存在量词命题
(真)
存在量词命题(假)
全称量词命题(真)
x∈M,p(x)为真:能在集合M中找出一个元素x,使p(x)成立;
x∈M,p(x)为假:在集合M中,使p(x)成立的元素x不存在.
判定一个存在量词命题的真假:
x∈M,p(x)为真:对集合M中每一个元素x,
都有p(x)成立;
x∈M,p(x)为假:在集合M中存在一个元素x,
使得p(x)不成立.
判定一个全称量词命题的真假:
例题2 判断下列命题的真假.
(1) x∈R,x2>x;
(2) x∈Q,x2-8=0;
(3) x∈R,x2+x+1>0;
(4) x∈{x|x是无理数},x2是无理数;
(5) a,b∈R,a2+b2≥2ab
真
假
真
真
真
量词
全称量词
存在量词
全称量词命题
存在量词命题
x∈M,p(x)
x∈M,p(x)
判断命题真假
如何判断全称量词命题与存在量词命题的真假
假命题
真命题
对任意x∈M
都有p(x)成立
存在x∈M
使得p(x)成立
x∈M,p(x)
x∈M,p(x)
存在x∈M使
得p(x)不成立
对任意x∈M
p(x)不成立
课后练习
1.下列命题中,不是全称量词命题的是( )
A.任何一个实数乘0都等于0
B.自然数都是正整数
C.对于任意x∈Z,2x+1是奇数
D.一定存在没有最大值的二次函数
D
2.下列命题中,存在量词命题的个数是( )
①有些自然数是偶数;
②正方形是菱形;
③能被6整除的数也能被3整除;
④对任意实数a,b,c关于x的方程ax2+bx+c=0都有两个实数解.
A.0 B.1
C.2 D.3
课后练习
B
3.下列命题是“ x∈R,x2>3”的另一种表述方法的是( )
A.有一个x∈R,使x2>3成立
B.对有些x∈R,使x2>3成立
C.任选一个x∈R,使x2>3成立
D.至少有一个x∈R,使x2>3成立
课后练习
C
4.对任意x>8,x>a恒成立,则实数a的取值范围是________.
课后练习
答案:a≤8
课后练习
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
