11.1.1三角形的边 课件(共26张PPT)
文档属性
| 名称 | 11.1.1三角形的边 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 20:50:15 | ||
图片预览





文档简介
(共26张PPT)
人教七上数学同步精品课件
人教版七年级上册
第十一章 三角形
11.1.1 三角形的边
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解三角形的定义,认识三角形的边、角、顶点;
2.能用符号语言表示三角形,能识别不同形状的三角形;
3.掌握三角形的三边关系,并能用它解决相关问题.
学习目标
重点
重点
难点
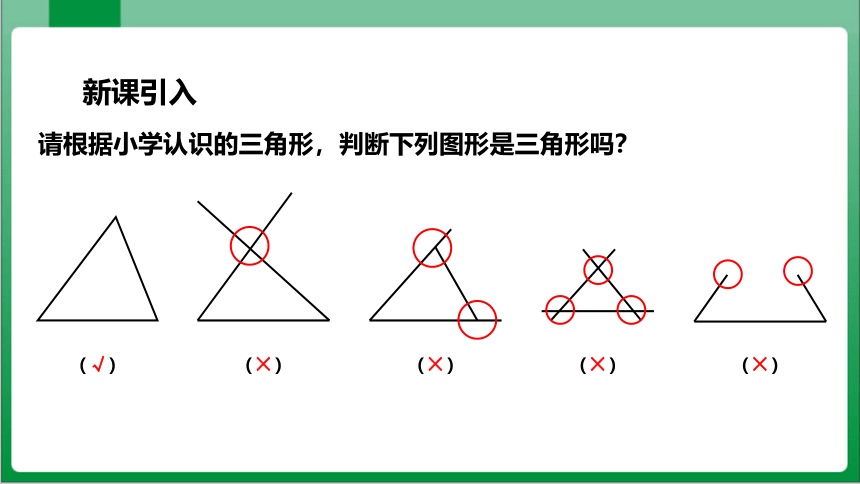
请根据小学认识的三角形,判断下列图形是三角形吗?
( )
( )
( )
( )
( )
√
×
×
×
×
新课引入
一 三角形的相关概念
A
B
C
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
边:如图,线段 AB,BC,CA 是三角形的边.
顶点:如图,点 A,B,C 是三角形的顶点.
角:如图,∠A,∠B,∠C 叫做三角形的内角,
简称三角形的角.
新知学习
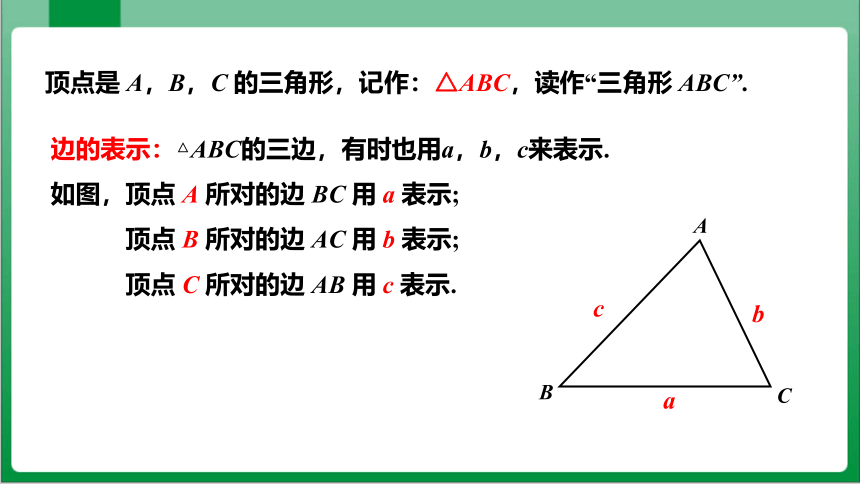
顶点是 A,B,C 的三角形,记作:△ABC,读作“三角形 ABC”.
A
B
C
a
b
c
边的表示:△ABC的三边,有时也用a,b,c来表示.
如图,顶点 A 所对的边 BC 用 a 表示;
顶点 B 所对的边 AC 用 b 表示;
顶点 C 所对的边 AB 用 c 表示.
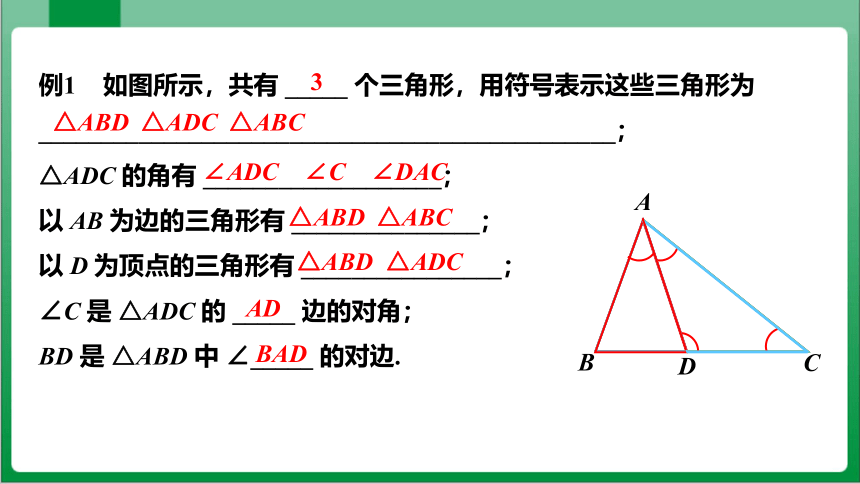
例1 如图所示,共有 _____ 个三角形,用符号表示这些三角形为 ______________________________________________;
△ADC 的角有 ___________________;
以 AB 为边的三角形有 _______________;
以 D 为顶点的三角形有 ________________;
∠C 是 △ADC 的 _____ 边的对角;
BD 是 △ABD 中 ∠_____ 的对边.
C
D
A
B
3
△ABD
△ADC
△ABC
∠ADC
∠C
∠DAC
△ABD
△ABC
△ABD
△ADC
AD
BAD
二 三角形的分类
我们知道:
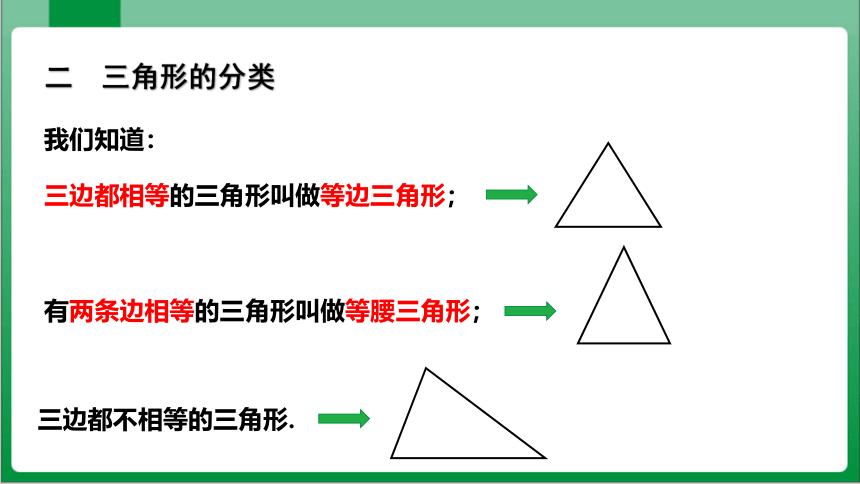
三边都不相等的三角形.
三边都相等的三角形叫做等边三角形;
有两条边相等的三角形叫做等腰三角形;
思考
如何按照边的关系对三角形进行分类呢?
以“是否有边相等”,可以将三角形分为两类:
三边都
不相等
的三角形
等腰
三角形
等边
三角形
三角形
三边都不相等的三角形
等腰三角形
等边三角形
底边和腰不相等的等腰三角形
是不是也可以按照角的大小对三角形分类呢?
观察下图,按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
∟
腰
腰
底边
顶角
底角
底角
在等腰三角形中:
腰:相等的两边都叫做腰;
底边:另一边叫做底边;
顶角:两腰的夹角叫做顶角;
底角:腰和底边的夹角叫做底角.
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
底边和腰相等
例1 判断下列说法是否正确.
①等腰三角形是等边三角形; ( )
②三角形按边可分为等腰三角形、等边三角形和不等边三角形; ( )
③等腰三角形至少有两边相等; ( )
④三角形按角可分为锐角三角形、直角三角形和钝角三角形. ( )
√
√
三 三角形的三边关系
探究
任意画一个△ABC,从点 B 出发,沿着三角形的边到点 C,有几条路线可以选择?各条路线的长有什么关系?能证明你的结论吗?
A
B
C
有2条路线可以选择,
分别是B → C, B → A → C.
AB + AC > BC.
A
B
C
对于任意一个△ABC,如果把其中任意两个顶点(例如B、C)看成定点,由“两点之间,线段最短”,得
AB + AC > BC, ①
同理,AC + BC > AB, ②
AB + BC > AC, ③
三角形任意两边之和大于第三边.
证明
三角形任意两边之差小于第三边.
AB + AC > BC, ①
AC + BC > AB, ②
AB + BC > AC, ③
由不等式②③移项可得:
BC > AB - AC,
BC > AC - AB.
A
B
C
例2 有两根长度分别为 5cm 和 8cm 的木棒,用长度为 2cm 的木棒与它们能组成三角形吗?为什么?长度为 13cm 的木棒呢?
分析: 5 + 8 > 2,
8 + 2 > 5,
5 + 2 < 8 .
√
√
×
5 + 8 = 13,
8 + 13 > 5,
5 + 13 > 8 .
×
√
√
发现:判断三条线段是否可以组成三角形,只需判断两条较短线段的和是否大于第三条线段即可.
不能.
不能.
1. 三角形两边的和大于第三边;
(可用来判断三条线段能否组成三角形:只需判断两条较短线段的和是否大于第三条线段即可)
2. 三角形两边的差小于第三边.
三角形的三边关系:
归纳
注意:由三角形的三边关系可得到,三角形第三边的取值范围:
两边的差 < 第三边 < 两边的和
例3 用一条长为 18 cm 的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的 2 倍,那么各边的长是多少?
解:(1) 设底边长为 x cm,则腰长为 2x cm,
x + 2x + 2x = 18,
解得 x = 3.6.
∴ 三边长分别为 3.6 cm、7.2 cm、7.2 cm.
解:(2) ∵ 长为 4 cm 的边可能是腰,也可能是底边,需要分情况讨论:
①若4 cm长的边为底边 ,设腰长为 x cm,则有
4 + 2x = 18, 解得 x = 7.
②若4 cm长的边为腰,设底边长为 x cm,则有
2×4 + x = 18, 解得 x = 10.
因为 4 + 4<10,不符合三角形两边的和大于第三边,所以不能围成腰长是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是 4 cm的等腰三角形.
(2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
1. 已知等腰三角形的两边长分别为 8 cm,3 cm,则这个三角形的周长为 _______.
19 cm
变式 已知等腰三角形的两边长分别为 8 cm,6 cm,则这个三角形的周长为 _____________.
20 cm或22cm
随堂练习
解:设第三根木棒长为 x,则应有
7 - 2 < x < 7 + 2,
即 5 < x < 9.
第三根木棒长的范围为 5 < x < 9.
2.一根木棒长为 7,另一根木棒长为 2,则第三根木棒长应在什么范围?
3.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
= - (a-b-c)-(b-c-a)+(c+a-b)
=-a+b+c-b+c+a+c+a-b
=3c+a-b.
分类
定义
顶点、角、边
按边分:三边都不相等的三角形和等腰三角形
按角分:锐角三角形、直角三角形、钝角三角形
1.判断三条线段能否组成三角形;
2.求第三边长或取值范围.
三角形
应用
三边关系
1. 三角形两边的和大于第三边;
2. 三角形两边的差小于第三边.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第十一章 三角形
11.1.1 三角形的边
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解三角形的定义,认识三角形的边、角、顶点;
2.能用符号语言表示三角形,能识别不同形状的三角形;
3.掌握三角形的三边关系,并能用它解决相关问题.
学习目标
重点
重点
难点
请根据小学认识的三角形,判断下列图形是三角形吗?
( )
( )
( )
( )
( )
√
×
×
×
×
新课引入
一 三角形的相关概念
A
B
C
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
边:如图,线段 AB,BC,CA 是三角形的边.
顶点:如图,点 A,B,C 是三角形的顶点.
角:如图,∠A,∠B,∠C 叫做三角形的内角,
简称三角形的角.
新知学习
顶点是 A,B,C 的三角形,记作:△ABC,读作“三角形 ABC”.
A
B
C
a
b
c
边的表示:△ABC的三边,有时也用a,b,c来表示.
如图,顶点 A 所对的边 BC 用 a 表示;
顶点 B 所对的边 AC 用 b 表示;
顶点 C 所对的边 AB 用 c 表示.
例1 如图所示,共有 _____ 个三角形,用符号表示这些三角形为 ______________________________________________;
△ADC 的角有 ___________________;
以 AB 为边的三角形有 _______________;
以 D 为顶点的三角形有 ________________;
∠C 是 △ADC 的 _____ 边的对角;
BD 是 △ABD 中 ∠_____ 的对边.
C
D
A
B
3
△ABD
△ADC
△ABC
∠ADC
∠C
∠DAC
△ABD
△ABC
△ABD
△ADC
AD
BAD
二 三角形的分类
我们知道:
三边都不相等的三角形.
三边都相等的三角形叫做等边三角形;
有两条边相等的三角形叫做等腰三角形;
思考
如何按照边的关系对三角形进行分类呢?
以“是否有边相等”,可以将三角形分为两类:
三边都
不相等
的三角形
等腰
三角形
等边
三角形
三角形
三边都不相等的三角形
等腰三角形
等边三角形
底边和腰不相等的等腰三角形
是不是也可以按照角的大小对三角形分类呢?
观察下图,按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
∟
腰
腰
底边
顶角
底角
底角
在等腰三角形中:
腰:相等的两边都叫做腰;
底边:另一边叫做底边;
顶角:两腰的夹角叫做顶角;
底角:腰和底边的夹角叫做底角.
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
底边和腰相等
例1 判断下列说法是否正确.
①等腰三角形是等边三角形; ( )
②三角形按边可分为等腰三角形、等边三角形和不等边三角形; ( )
③等腰三角形至少有两边相等; ( )
④三角形按角可分为锐角三角形、直角三角形和钝角三角形. ( )
√
√
三 三角形的三边关系
探究
任意画一个△ABC,从点 B 出发,沿着三角形的边到点 C,有几条路线可以选择?各条路线的长有什么关系?能证明你的结论吗?
A
B
C
有2条路线可以选择,
分别是B → C, B → A → C.
AB + AC > BC.
A
B
C
对于任意一个△ABC,如果把其中任意两个顶点(例如B、C)看成定点,由“两点之间,线段最短”,得
AB + AC > BC, ①
同理,AC + BC > AB, ②
AB + BC > AC, ③
三角形任意两边之和大于第三边.
证明
三角形任意两边之差小于第三边.
AB + AC > BC, ①
AC + BC > AB, ②
AB + BC > AC, ③
由不等式②③移项可得:
BC > AB - AC,
BC > AC - AB.
A
B
C
例2 有两根长度分别为 5cm 和 8cm 的木棒,用长度为 2cm 的木棒与它们能组成三角形吗?为什么?长度为 13cm 的木棒呢?
分析: 5 + 8 > 2,
8 + 2 > 5,
5 + 2 < 8 .
√
√
×
5 + 8 = 13,
8 + 13 > 5,
5 + 13 > 8 .
×
√
√
发现:判断三条线段是否可以组成三角形,只需判断两条较短线段的和是否大于第三条线段即可.
不能.
不能.
1. 三角形两边的和大于第三边;
(可用来判断三条线段能否组成三角形:只需判断两条较短线段的和是否大于第三条线段即可)
2. 三角形两边的差小于第三边.
三角形的三边关系:
归纳
注意:由三角形的三边关系可得到,三角形第三边的取值范围:
两边的差 < 第三边 < 两边的和
例3 用一条长为 18 cm 的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的 2 倍,那么各边的长是多少?
解:(1) 设底边长为 x cm,则腰长为 2x cm,
x + 2x + 2x = 18,
解得 x = 3.6.
∴ 三边长分别为 3.6 cm、7.2 cm、7.2 cm.
解:(2) ∵ 长为 4 cm 的边可能是腰,也可能是底边,需要分情况讨论:
①若4 cm长的边为底边 ,设腰长为 x cm,则有
4 + 2x = 18, 解得 x = 7.
②若4 cm长的边为腰,设底边长为 x cm,则有
2×4 + x = 18, 解得 x = 10.
因为 4 + 4<10,不符合三角形两边的和大于第三边,所以不能围成腰长是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是 4 cm的等腰三角形.
(2) 能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
1. 已知等腰三角形的两边长分别为 8 cm,3 cm,则这个三角形的周长为 _______.
19 cm
变式 已知等腰三角形的两边长分别为 8 cm,6 cm,则这个三角形的周长为 _____________.
20 cm或22cm
随堂练习
解:设第三根木棒长为 x,则应有
7 - 2 < x < 7 + 2,
即 5 < x < 9.
第三根木棒长的范围为 5 < x < 9.
2.一根木棒长为 7,另一根木棒长为 2,则第三根木棒长应在什么范围?
3.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
= - (a-b-c)-(b-c-a)+(c+a-b)
=-a+b+c-b+c+a+c+a-b
=3c+a-b.
分类
定义
顶点、角、边
按边分:三边都不相等的三角形和等腰三角形
按角分:锐角三角形、直角三角形、钝角三角形
1.判断三条线段能否组成三角形;
2.求第三边长或取值范围.
三角形
应用
三边关系
1. 三角形两边的和大于第三边;
2. 三角形两边的差小于第三边.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
