11.2.1 三角形的内角第1课时 三角形的内角和定理课件(共27张PPT)
文档属性
| 名称 | 11.2.1 三角形的内角第1课时 三角形的内角和定理课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 16:16:26 | ||
图片预览






文档简介
(共27张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十一章 三角形
11.2.1 三角形的内角
第1课时 三角形的内角和定理
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索并证明三角形内角和定理.
2. 能运用三角形内角和定理解决简单问题.
学习目标
重点
难点
请同学们准备好三角形纸片、剪刀、量角器、直尺.
在小学我们已经知道任意一个三角形的三个内角和等于 180°,你还记得是怎么发现这个结论的吗?
请大家利用手中的三角形纸片进行探究.
新课引入
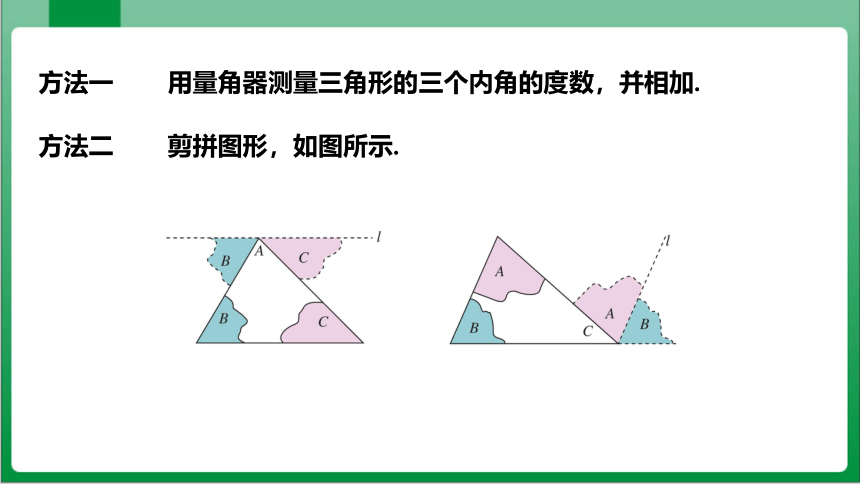
方法一 用量角器测量三角形的三个内角的度数,并相加.
方法二 剪拼图形,如图所示.
该怎么证明呢?
通过度量或剪拼的方法,可以验证三角形的内角和等于180°.但是,由于测量常常有误差,这种“验证”不是“数学证明”,不能完全让人信服;又由于形状不同的三角形有无数个,我们不可能用上述方法一一验证所有三角形的内角和等于180°.所以,需要通过推理的方法去证明:任意一个三角形的内角和一定等于180°.
一、三角形内角和定理
新知学习
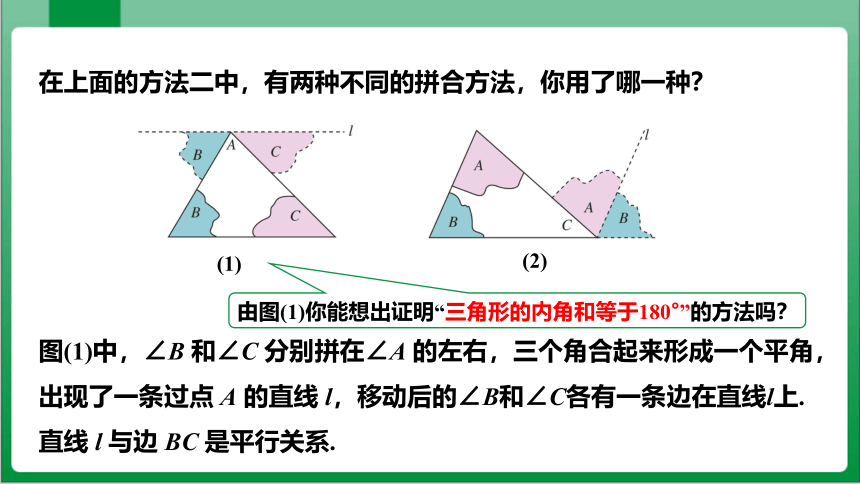
由图(1)你能想出证明“三角形的内角和等于180°”的方法吗?
在上面的方法二中,有两种不同的拼合方法,你用了哪一种?
(1)
(2)
图(1)中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点 A 的直线 l,移动后的∠B和∠C各有一条边在直线l上.直线 l 与边 BC 是平行关系.
A
B
C
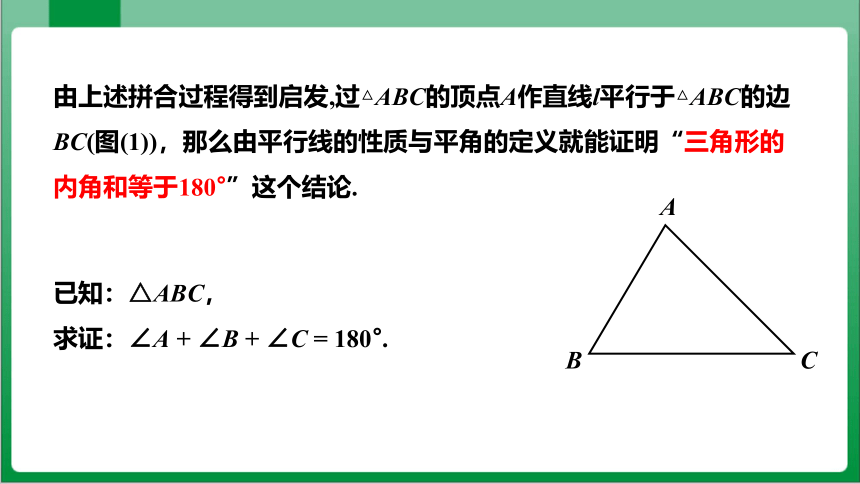
已知:△ABC,
求证:∠A + ∠B + ∠C = 180°.
由上述拼合过程得到启发,过△ABC的顶点A作直线l平行于△ABC的边BC(图(1)),那么由平行线的性质与平角的定义就能证明“三角形的内角和等于180°”这个结论.
证明:如图,过点 A 作直线 l,使l ∥ BC,
∵ l ∥ BC,
∴∠2 =∠4 ( 两直线平行,内错角相等 ).
同理∠3 =∠5.
∵∠1,∠4,∠5 组成平角,
∴∠1+∠4+∠5 = 180° ( 平角定义 ).
∴∠1+∠2+∠3 = 180° ( 等量代换 ).
l
A
C
B
1
2
3
4
5
三角形内角和定理:三角形三个内角的和等于 180° .
A
B
C
符号语言:
在△ABC 中,
∠A +∠B +∠C = 180°.
如图(2),将剪下的两个角拼在了第三个角的同一侧,这样也能形成一个平角.
你能模仿前面的证明过程,用图(2)的方法证明此定理吗
l
A
C
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
证明:如图,延长 BC,过点 C 作直线 l,使 l // AB .
∵ l //AB,
∴∠1 =∠4 ( 两直线平行,内错角相等 ),
∠2 =∠5 ( 两直线平行,同位角相等 ).
∵∠3,∠4,∠5 组成平角.
∴∠3 +∠4 +∠5 = 180° ( 平角定义 ).
∴∠1 +∠2 +∠3 = 180° ( 等量代换 ).
例1 如图,在△ABC 中,∠BAC = 40°,∠B = 75°,AD 是△ABC 的角平分线,求∠ADB 的度数.
A
C
B
D
解:由∠BAC = 40°,AD 是△ABC 的角平分线,得
∠BAD = ∠BAC = 20°
在△ABD 中,
∠ADB = 180° -∠B -∠BAD
=180° - 75° - 20° = 85° .
二 三角形内角和的应用
例2 下图是 A,B,C 三岛的平面图,C 岛在 A 岛的北偏东 50° 方向,B 岛在 A 岛的北偏东 80° 方向,C 岛在 B 岛的北偏西 40° 方向. 从 B 岛看 A,C 两岛的视角∠ABC 是多少度?从 C 岛看 A,B 两岛的视角∠ACB 呢?
A
C
B
D
E
北
北
50°
80°
40°
分析:A,B,C 三岛的连线构成△ABC,所求的∠ACB 是△ABC 的一个内角.如果能求出∠CAB,∠ABC,就能求出∠ACB.
解:∠CAB =∠BAD -∠CAD = 80° - 50° = 30°.
由 AD // BE,得∠BAD +∠ABE = 180° .
所以∠ABE = 180° -∠BAD = 180°-80° = 100°,
∠ABC =∠ABE -∠EBC = 100° - 40° = 60°.
在△ABC 中,
∠ACB = 180° -∠ABC -∠CAB = 180° - 60° - 30° = 90°
A
C
B
D
E
北
北
50°
80°
40°
答:从 B 岛看 A,C 两岛的视角∠ABC 是 60°,从 C 岛看 A,B 两岛的视角∠ACB 是 90°.
你还能想出其他解法吗?
A
C
B
D
E
北
北
50°
80°
40°
F
添加辅助线
分析:过点 C 作 CF // AD,则 CF// BE,
可得∠ACF =∠DAC = 50°,
∠BCF =∠CBE = 40°,
所以∠ACB =∠ACF +∠BCF = 90°.
∠CAB=∠DAB-∠DAC=30°,
所以∠ABC=180°-∠CAB-∠ACB=60°.
解法二:
同学们自己动手写出解法吧~
1.如图,从 A 处观测 C 处的仰角∠CAD = 30°,从 B 处观测 C 处的仰角∠CBD = 45°. 从 C 处观测 A,B 两处的视角∠ACB 是多少
∟
A
C
B
D
30°
45°
针对训练
解:∵∠CBD = 45°,
∴∠ABC = 180° - ∠CBD = 135° .
在△ABC 中,∠CAB = 30°,
根据三角形内角和定理,
∠ACB = 180° -∠CAB -∠ABC = 180°-30°-135°=15° .
还有其他解法吗?
∟
A
C
B
D
30°
45°
解法二:∵∠CBD = 45°,
∴∠BCD = 180° - ∠D-∠CBD =180° - 90 ° - 45°=45° .
在△ADC 中,∠CAD = 30°,
∴∠ACD = 180° - ∠D-∠CAD =180° - 90 ° - 30°=60° .
∴∠ACB = ∠ACD -∠BCD = 60°-45°=15° .
1. 在△ABC 中,∠A∶∠B∶∠C=1∶2∶3,则△ABC 是_______三角形.
2. 在△ABC 中,∠A =∠B + 10°,∠C =∠A + 10°,则∠A = °, ∠B = °,∠C = °.
直角
60
50
70
随堂练习
3.如图,一种滑翔伞的形状是左右对称的四边形 ABCD,其中∠A = 150°, ∠B =∠D = 40°,求∠BCD 的度数.
A
C
B
D
150°
40°
40°
分析:由四边形 ABCD 左右对称得∠BAC =∠DAC = 75°,由∠ACB = 180° -∠BAC -∠B,求出∠ACB 的度数.
A
C
B
D
150°
40°
40°
解: ∵四边形 ABCD 左右对称,
∴∠BAC =∠DAC = 75°.
∴∠ACB = 180° -∠BAC -∠B,
= 180° - 75° - 40°
= 65°.
∴∠ BCD = 2∠ACB = 2×65° = 130°.
4.如图,在△ABC 中,BP 平分∠ABC,CP 平分∠ACB.
(1)若∠A = 60°,求∠BPC 的度数.
解:在△ABC 中,∵∠A = 60°,
∴∠ABC +∠ACB = 120°.
∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB) = 60°.
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - 60° = 120°.
解:∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB).
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - (∠ABC +∠ACB)
= 180° - (180° - ∠A)
= 90° + ∠A.
(2) 你能直接写出∠BPC 与∠A 之间的数量关系吗?
1. 三角形内角和定理是什么?
2. 三角形内角和定理如何推导?
三角形三个内角的和等于 180°.
通过构造平角,利用平行线的性质转移角,利用平角的定义得到 180°.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十一章 三角形
11.2.1 三角形的内角
第1课时 三角形的内角和定理
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索并证明三角形内角和定理.
2. 能运用三角形内角和定理解决简单问题.
学习目标
重点
难点
请同学们准备好三角形纸片、剪刀、量角器、直尺.
在小学我们已经知道任意一个三角形的三个内角和等于 180°,你还记得是怎么发现这个结论的吗?
请大家利用手中的三角形纸片进行探究.
新课引入
方法一 用量角器测量三角形的三个内角的度数,并相加.
方法二 剪拼图形,如图所示.
该怎么证明呢?
通过度量或剪拼的方法,可以验证三角形的内角和等于180°.但是,由于测量常常有误差,这种“验证”不是“数学证明”,不能完全让人信服;又由于形状不同的三角形有无数个,我们不可能用上述方法一一验证所有三角形的内角和等于180°.所以,需要通过推理的方法去证明:任意一个三角形的内角和一定等于180°.
一、三角形内角和定理
新知学习
由图(1)你能想出证明“三角形的内角和等于180°”的方法吗?
在上面的方法二中,有两种不同的拼合方法,你用了哪一种?
(1)
(2)
图(1)中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点 A 的直线 l,移动后的∠B和∠C各有一条边在直线l上.直线 l 与边 BC 是平行关系.
A
B
C
已知:△ABC,
求证:∠A + ∠B + ∠C = 180°.
由上述拼合过程得到启发,过△ABC的顶点A作直线l平行于△ABC的边BC(图(1)),那么由平行线的性质与平角的定义就能证明“三角形的内角和等于180°”这个结论.
证明:如图,过点 A 作直线 l,使l ∥ BC,
∵ l ∥ BC,
∴∠2 =∠4 ( 两直线平行,内错角相等 ).
同理∠3 =∠5.
∵∠1,∠4,∠5 组成平角,
∴∠1+∠4+∠5 = 180° ( 平角定义 ).
∴∠1+∠2+∠3 = 180° ( 等量代换 ).
l
A
C
B
1
2
3
4
5
三角形内角和定理:三角形三个内角的和等于 180° .
A
B
C
符号语言:
在△ABC 中,
∠A +∠B +∠C = 180°.
如图(2),将剪下的两个角拼在了第三个角的同一侧,这样也能形成一个平角.
你能模仿前面的证明过程,用图(2)的方法证明此定理吗
l
A
C
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
证明:如图,延长 BC,过点 C 作直线 l,使 l // AB .
∵ l //AB,
∴∠1 =∠4 ( 两直线平行,内错角相等 ),
∠2 =∠5 ( 两直线平行,同位角相等 ).
∵∠3,∠4,∠5 组成平角.
∴∠3 +∠4 +∠5 = 180° ( 平角定义 ).
∴∠1 +∠2 +∠3 = 180° ( 等量代换 ).
例1 如图,在△ABC 中,∠BAC = 40°,∠B = 75°,AD 是△ABC 的角平分线,求∠ADB 的度数.
A
C
B
D
解:由∠BAC = 40°,AD 是△ABC 的角平分线,得
∠BAD = ∠BAC = 20°
在△ABD 中,
∠ADB = 180° -∠B -∠BAD
=180° - 75° - 20° = 85° .
二 三角形内角和的应用
例2 下图是 A,B,C 三岛的平面图,C 岛在 A 岛的北偏东 50° 方向,B 岛在 A 岛的北偏东 80° 方向,C 岛在 B 岛的北偏西 40° 方向. 从 B 岛看 A,C 两岛的视角∠ABC 是多少度?从 C 岛看 A,B 两岛的视角∠ACB 呢?
A
C
B
D
E
北
北
50°
80°
40°
分析:A,B,C 三岛的连线构成△ABC,所求的∠ACB 是△ABC 的一个内角.如果能求出∠CAB,∠ABC,就能求出∠ACB.
解:∠CAB =∠BAD -∠CAD = 80° - 50° = 30°.
由 AD // BE,得∠BAD +∠ABE = 180° .
所以∠ABE = 180° -∠BAD = 180°-80° = 100°,
∠ABC =∠ABE -∠EBC = 100° - 40° = 60°.
在△ABC 中,
∠ACB = 180° -∠ABC -∠CAB = 180° - 60° - 30° = 90°
A
C
B
D
E
北
北
50°
80°
40°
答:从 B 岛看 A,C 两岛的视角∠ABC 是 60°,从 C 岛看 A,B 两岛的视角∠ACB 是 90°.
你还能想出其他解法吗?
A
C
B
D
E
北
北
50°
80°
40°
F
添加辅助线
分析:过点 C 作 CF // AD,则 CF// BE,
可得∠ACF =∠DAC = 50°,
∠BCF =∠CBE = 40°,
所以∠ACB =∠ACF +∠BCF = 90°.
∠CAB=∠DAB-∠DAC=30°,
所以∠ABC=180°-∠CAB-∠ACB=60°.
解法二:
同学们自己动手写出解法吧~
1.如图,从 A 处观测 C 处的仰角∠CAD = 30°,从 B 处观测 C 处的仰角∠CBD = 45°. 从 C 处观测 A,B 两处的视角∠ACB 是多少
∟
A
C
B
D
30°
45°
针对训练
解:∵∠CBD = 45°,
∴∠ABC = 180° - ∠CBD = 135° .
在△ABC 中,∠CAB = 30°,
根据三角形内角和定理,
∠ACB = 180° -∠CAB -∠ABC = 180°-30°-135°=15° .
还有其他解法吗?
∟
A
C
B
D
30°
45°
解法二:∵∠CBD = 45°,
∴∠BCD = 180° - ∠D-∠CBD =180° - 90 ° - 45°=45° .
在△ADC 中,∠CAD = 30°,
∴∠ACD = 180° - ∠D-∠CAD =180° - 90 ° - 30°=60° .
∴∠ACB = ∠ACD -∠BCD = 60°-45°=15° .
1. 在△ABC 中,∠A∶∠B∶∠C=1∶2∶3,则△ABC 是_______三角形.
2. 在△ABC 中,∠A =∠B + 10°,∠C =∠A + 10°,则∠A = °, ∠B = °,∠C = °.
直角
60
50
70
随堂练习
3.如图,一种滑翔伞的形状是左右对称的四边形 ABCD,其中∠A = 150°, ∠B =∠D = 40°,求∠BCD 的度数.
A
C
B
D
150°
40°
40°
分析:由四边形 ABCD 左右对称得∠BAC =∠DAC = 75°,由∠ACB = 180° -∠BAC -∠B,求出∠ACB 的度数.
A
C
B
D
150°
40°
40°
解: ∵四边形 ABCD 左右对称,
∴∠BAC =∠DAC = 75°.
∴∠ACB = 180° -∠BAC -∠B,
= 180° - 75° - 40°
= 65°.
∴∠ BCD = 2∠ACB = 2×65° = 130°.
4.如图,在△ABC 中,BP 平分∠ABC,CP 平分∠ACB.
(1)若∠A = 60°,求∠BPC 的度数.
解:在△ABC 中,∵∠A = 60°,
∴∠ABC +∠ACB = 120°.
∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB) = 60°.
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - 60° = 120°.
解:∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB).
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - (∠ABC +∠ACB)
= 180° - (180° - ∠A)
= 90° + ∠A.
(2) 你能直接写出∠BPC 与∠A 之间的数量关系吗?
1. 三角形内角和定理是什么?
2. 三角形内角和定理如何推导?
三角形三个内角的和等于 180°.
通过构造平角,利用平行线的性质转移角,利用平角的定义得到 180°.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
