11.2.2三角形的外角 课件(共26张PPT)
文档属性
| 名称 | 11.2.2三角形的外角 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十一章 三角形
11.2.2 三角形的外角
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 了解三角形外角的概念和三角形外角的性质.
2. 了解三角形的外角和.
重点
重点
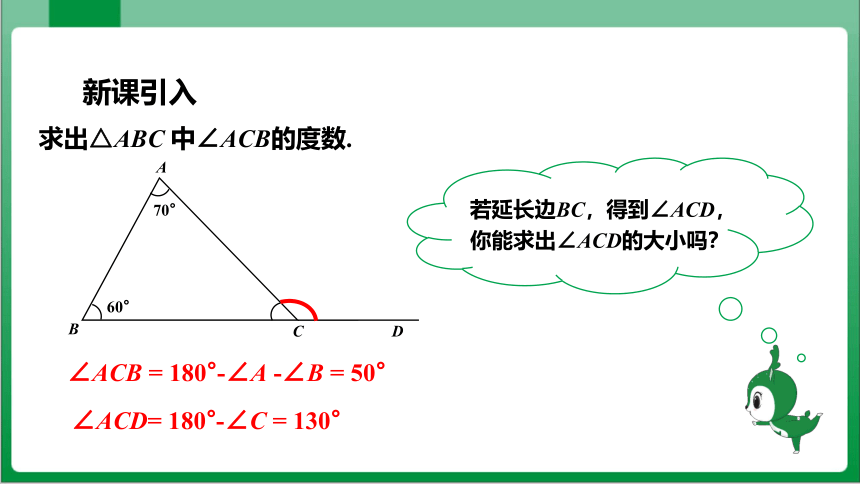
求出△ABC 中∠ACB的度数.
若延长边BC,得到∠ACD,你能求出∠ACD的大小吗?
60°
70°
B
A
C
∠ACB = 180°-∠A -∠B = 50°
D
∠ACD= 180°-∠C = 130°
新课引入
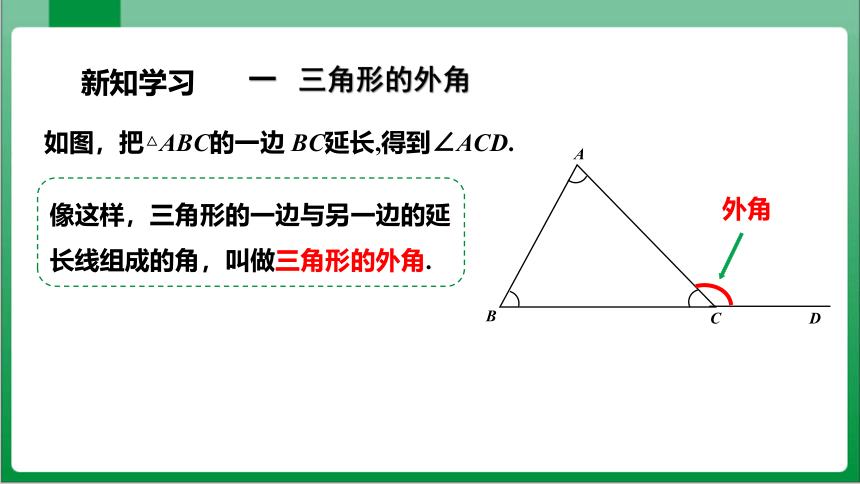
像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
一 三角形的外角
B
A
C
D
外角
如图,把△ABC的一边 BC延长,得到∠ACD.
新知学习
D
C
B
A
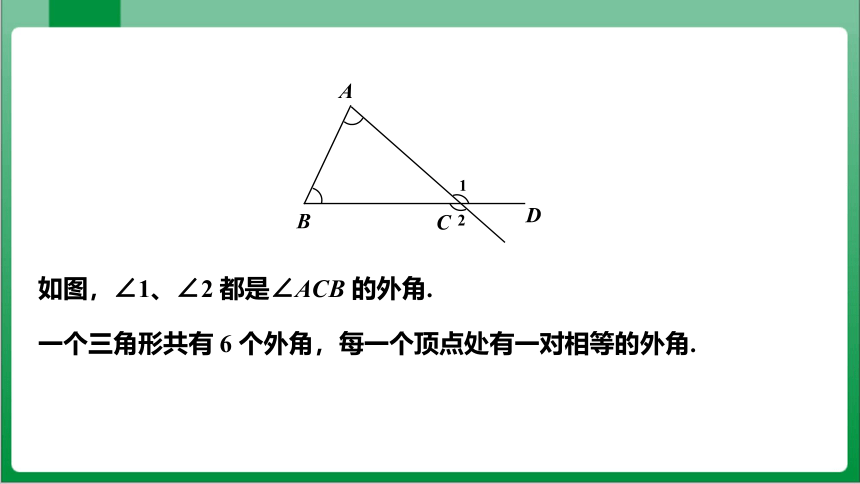
如图,∠1、∠2 都是∠ACB 的外角.
1
2
一个三角形共有 6 个外角,每一个顶点处有一对相等的外角.
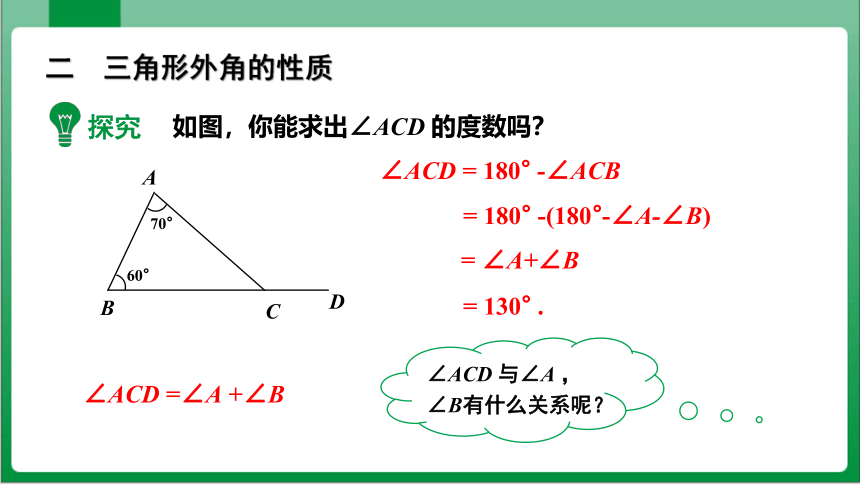
如图,你能求出∠ACD 的度数吗?
D
C
B
A
60°
70°
∠ACD = 180° -∠ACB
= 180° -(180°-∠A-∠B)
= ∠A+∠B
= 130° .
∠ACD 与∠A ,∠B有什么关系呢?
探究
∠ACD =∠A +∠B
二 三角形外角的性质
D
C
B
A
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
已知: ∠ACD 是△ABC 的一个外角,
求证: ∠ACD =∠A +∠B.
探究
证明:
∵∠A +∠B +∠ACB = 180°
∴∠ACB = 180° -∠A -∠B
∵∠ACB +∠ACD = 180°
∴∠ACD = 180° -∠ACB
=180 - ( 180° -∠A -∠B)
= ∠A +∠B.
D
C
B
A
证明
还有其他证明方法吗?
l
A
C
B
1
2
3
4
5
证明:如图,过点 C 作直线 l,使 l // AB .
∵ l //AB,
∴∠1 =∠4 ( 两直线平行,内错角相等 ),
∠2 =∠5 ( 两直线平行,同位角相等 ).
∵∠ACD = ∠4 +∠5.
∴∠ACD = ∠1+∠2.
即∠ACD = ∠A +∠B.
D
一般地,由三角形内角和定理可以推出下面的推论:
三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
符号语言
∵∠ACD 是△ABC 的外角,
∴∠ACD = ∠A +∠B.
D
C
B
A
例1 如图,请回答:
(1) ∠1 = _________ + _________;
(2) ∠2 = _________ + _________.
D
C
B
A
1
4
3
2
∠3
∠4
∠C
∠CAD
例2 如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角,它们的和是多少?
D
C
B
A
1
3
2
E
F
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
三 三角形的外角和
∴∠BAE +∠CBD +∠ACD= 2(∠1 +∠2 +∠3).
由∠1 +∠2 +∠3 = 180°,得
∴ ∠BAE +∠CBF +∠ACD =2× 180°=360°.
D
C
B
A
1
3
2
E
F
你还有其他解法吗?
D
C
B
A
1
3
2
E
F
解法二:由∠1 +∠BAE = 180°,
∠2 +∠CBF = 180°,
∠3 +∠ACD = 180°,
得∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD = 540°,
由∠1 +∠2 +∠3 = 180°,
得∠BAE +∠CBF +∠ACD = 540° - 180° = 360°.
D
C
B
A
1
3
2
E
F
三角形的每个顶点处有两个外角,它们相等,所以每个顶点处只取一个外角(按同一个方向取三个角),把它们的和叫做三角形的外角和.
三角形的外角和等于 360°.
归纳
1.判断题:
1.三角形的外角和是指三角形所有外角的和.( )
2.三角形的外角和等于它内角和的2倍.( )
3.三角形的一个外角等于两个内角的和.( )
针对训练
1. 如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
A
B
C
D
E
解:如图,∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中,
∠C+∠1+∠2=180 ,
1
2
F
G
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180 .
随堂练习
分析:延长 BP 交 AC 于 点E 或连接 AP 并延长,构造三角形的外角,即可求出∠A 的度数.
E
2.如图,P 为△ABC 内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A 的度数.
解:延长 BP 交 AC 于点 E,
则∠BPC,∠PEC 分别为△PCE,△ABE 的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A.
∴∠PEC=∠BPC-∠PCE
=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
E
变式 如图,∠A = 51°,∠B = 20°,∠C = 30°,求∠BDC 的度数.
解法一:连接 AD 并延长,如图,
在△ABD 中,∠1 +∠B =∠3,
在△ACD 中,∠2 +∠C =∠4.
∵∠BDC =∠3 +∠4,
=∠1 +∠B+∠2 +∠C
=∠BAC +∠B +∠C
= 51° + 20° + 30° = 101°.
E
)
)
1
2
)
3
)
4
A
B
C
D
解法二:延长 BD 交 AC 于点 E,如图,
在△ABE 中,∠1 =∠B +∠A,
在△ECD 中,∠BDC =∠1 +∠C.
∴∠BDC =∠A +∠B +∠C
= 51° + 20° + 30° = 101°.
解法三:延长 CD 交 AB 于点 F ,如图(解题过程同解法二).
A
B
C
D
E
)
1
A
B
C
D
)
2
F
1. 三角形的外角的定义.
2. 三角形的外角定理
3. 三角形的外角和等于多少度?
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角和等于360°.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十一章 三角形
11.2.2 三角形的外角
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 了解三角形外角的概念和三角形外角的性质.
2. 了解三角形的外角和.
重点
重点
求出△ABC 中∠ACB的度数.
若延长边BC,得到∠ACD,你能求出∠ACD的大小吗?
60°
70°
B
A
C
∠ACB = 180°-∠A -∠B = 50°
D
∠ACD= 180°-∠C = 130°
新课引入
像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
一 三角形的外角
B
A
C
D
外角
如图,把△ABC的一边 BC延长,得到∠ACD.
新知学习
D
C
B
A
如图,∠1、∠2 都是∠ACB 的外角.
1
2
一个三角形共有 6 个外角,每一个顶点处有一对相等的外角.
如图,你能求出∠ACD 的度数吗?
D
C
B
A
60°
70°
∠ACD = 180° -∠ACB
= 180° -(180°-∠A-∠B)
= ∠A+∠B
= 130° .
∠ACD 与∠A ,∠B有什么关系呢?
探究
∠ACD =∠A +∠B
二 三角形外角的性质
D
C
B
A
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
已知: ∠ACD 是△ABC 的一个外角,
求证: ∠ACD =∠A +∠B.
探究
证明:
∵∠A +∠B +∠ACB = 180°
∴∠ACB = 180° -∠A -∠B
∵∠ACB +∠ACD = 180°
∴∠ACD = 180° -∠ACB
=180 - ( 180° -∠A -∠B)
= ∠A +∠B.
D
C
B
A
证明
还有其他证明方法吗?
l
A
C
B
1
2
3
4
5
证明:如图,过点 C 作直线 l,使 l // AB .
∵ l //AB,
∴∠1 =∠4 ( 两直线平行,内错角相等 ),
∠2 =∠5 ( 两直线平行,同位角相等 ).
∵∠ACD = ∠4 +∠5.
∴∠ACD = ∠1+∠2.
即∠ACD = ∠A +∠B.
D
一般地,由三角形内角和定理可以推出下面的推论:
三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
符号语言
∵∠ACD 是△ABC 的外角,
∴∠ACD = ∠A +∠B.
D
C
B
A
例1 如图,请回答:
(1) ∠1 = _________ + _________;
(2) ∠2 = _________ + _________.
D
C
B
A
1
4
3
2
∠3
∠4
∠C
∠CAD
例2 如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角,它们的和是多少?
D
C
B
A
1
3
2
E
F
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
三 三角形的外角和
∴∠BAE +∠CBD +∠ACD= 2(∠1 +∠2 +∠3).
由∠1 +∠2 +∠3 = 180°,得
∴ ∠BAE +∠CBF +∠ACD =2× 180°=360°.
D
C
B
A
1
3
2
E
F
你还有其他解法吗?
D
C
B
A
1
3
2
E
F
解法二:由∠1 +∠BAE = 180°,
∠2 +∠CBF = 180°,
∠3 +∠ACD = 180°,
得∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD = 540°,
由∠1 +∠2 +∠3 = 180°,
得∠BAE +∠CBF +∠ACD = 540° - 180° = 360°.
D
C
B
A
1
3
2
E
F
三角形的每个顶点处有两个外角,它们相等,所以每个顶点处只取一个外角(按同一个方向取三个角),把它们的和叫做三角形的外角和.
三角形的外角和等于 360°.
归纳
1.判断题:
1.三角形的外角和是指三角形所有外角的和.( )
2.三角形的外角和等于它内角和的2倍.( )
3.三角形的一个外角等于两个内角的和.( )
针对训练
1. 如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
A
B
C
D
E
解:如图,∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中,
∠C+∠1+∠2=180 ,
1
2
F
G
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180 .
随堂练习
分析:延长 BP 交 AC 于 点E 或连接 AP 并延长,构造三角形的外角,即可求出∠A 的度数.
E
2.如图,P 为△ABC 内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A 的度数.
解:延长 BP 交 AC 于点 E,
则∠BPC,∠PEC 分别为△PCE,△ABE 的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A.
∴∠PEC=∠BPC-∠PCE
=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
E
变式 如图,∠A = 51°,∠B = 20°,∠C = 30°,求∠BDC 的度数.
解法一:连接 AD 并延长,如图,
在△ABD 中,∠1 +∠B =∠3,
在△ACD 中,∠2 +∠C =∠4.
∵∠BDC =∠3 +∠4,
=∠1 +∠B+∠2 +∠C
=∠BAC +∠B +∠C
= 51° + 20° + 30° = 101°.
E
)
)
1
2
)
3
)
4
A
B
C
D
解法二:延长 BD 交 AC 于点 E,如图,
在△ABE 中,∠1 =∠B +∠A,
在△ECD 中,∠BDC =∠1 +∠C.
∴∠BDC =∠A +∠B +∠C
= 51° + 20° + 30° = 101°.
解法三:延长 CD 交 AB 于点 F ,如图(解题过程同解法二).
A
B
C
D
E
)
1
A
B
C
D
)
2
F
1. 三角形的外角的定义.
2. 三角形的外角定理
3. 三角形的外角和等于多少度?
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角和等于360°.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
