11.3.2多边形的内角和 课件(共27张PPT)
文档属性
| 名称 | 11.3.2多边形的内角和 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 08:53:59 | ||
图片预览






文档简介
(共27张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十一章 三角形
11.3.2 多边形的内角和
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.经历探索多边形的内角和与外角和公式的过程.
2.学会运用多边形的内角和与外角和公式解决问题.
学习目标
重点
难点
那任意一个
四边形呢?
1.你知道三角形内角和是多少度吗?
三角形内角和等于180°.
长方形和正方形的内角和都是360°.
2.你知道长方形和正方形的内角和是多少度吗?
新课引入
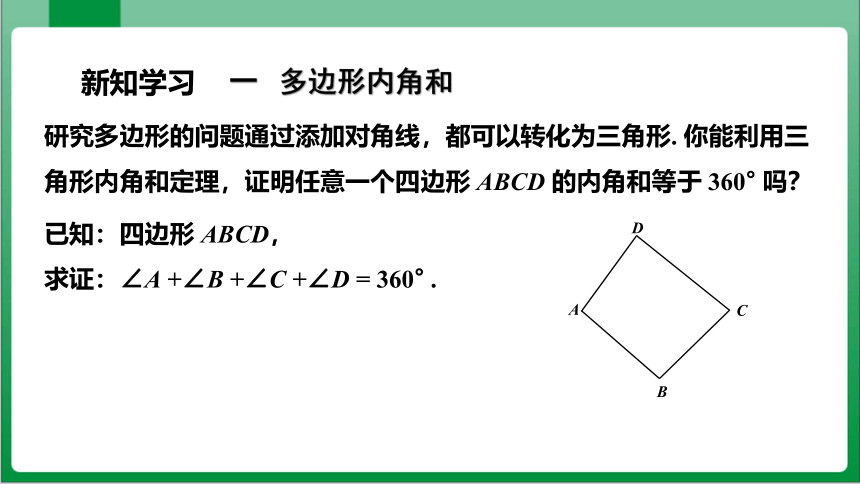
研究多边形的问题通过添加对角线,都可以转化为三角形. 你能利用三角形内角和定理,证明任意一个四边形 ABCD 的内角和等于 360° 吗?
已知:四边形 ABCD,
求证:∠A +∠B +∠C +∠D = 360° .
D
C
A
B
一 多边形内角和
新知学习
已知:四边形 ABCD,
求证:∠A +∠B +∠C +∠D = 360° .
D
C
A
B
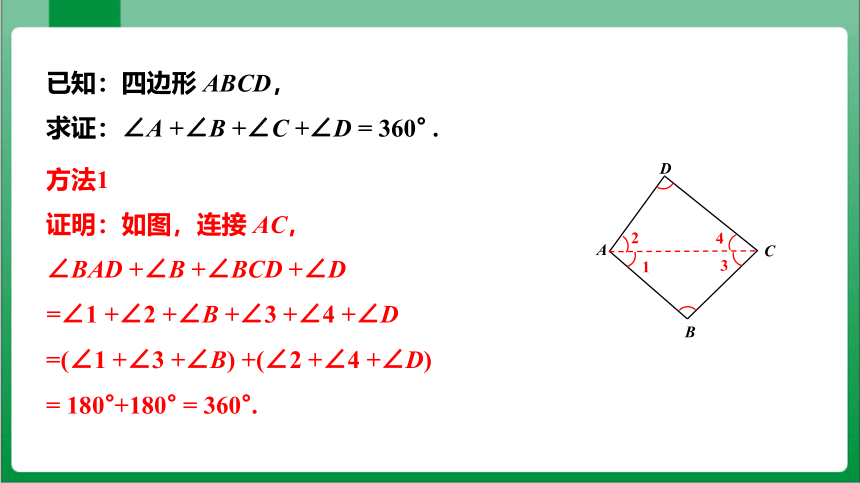
方法1
证明:如图,连接 AC,
∠BAD +∠B +∠BCD +∠D
=∠1 +∠2 +∠B +∠3 +∠4 +∠D
=(∠1 +∠3 +∠B) +(∠2 +∠4 +∠D)
= 180°+180° = 360°.
1
2
3
4
方法2
证明:如图,在四边形内部取一点 O,连接 OA,OB,OC,OD,把四边形分成四个三角形.
所以四边形 ABCD 的内角和
= 180°×4 - (∠AOB +∠AOD +∠COD +∠COB)
= 180°×4 - 360°
= 360°.
D
C
A
B
O
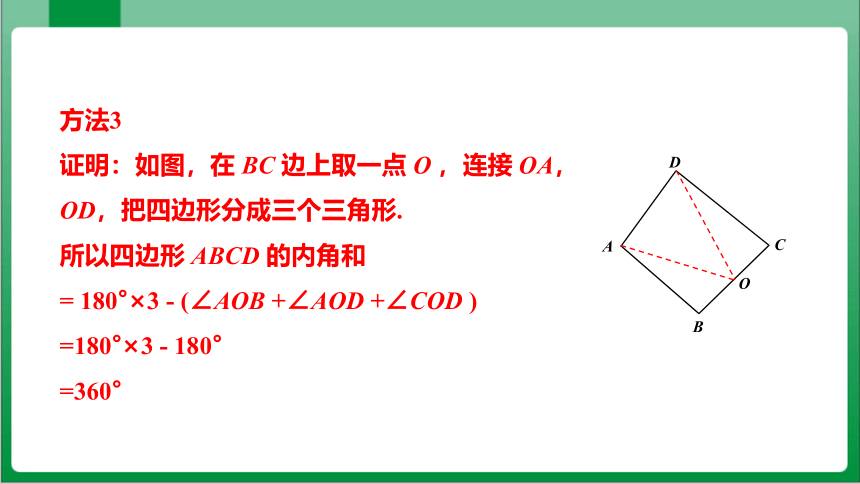
方法3
证明:如图,在 BC 边上取一点 O ,连接 OA,OD,把四边形分成三个三角形.
所以四边形 ABCD 的内角和
= 180°×3 - (∠AOB +∠AOD +∠COD )
=180°×3 - 180°
=360°
D
C
A
B
O
方法4
证明:如图,在四边形外任取一点 O,连接 OA,OB,OC,OD,把四边形转化为有一个公共顶点的三个三角形.
所以四边形 ABCD 的内角和
= 180°×3 - (∠COB +∠CBO +∠BCO )
= 180°×3 - 180°
= 360°
D
C
A
B
O
以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为已学的三角形内角和进行求解.
类比上面的过程,你能推导出五边形和六边形的内角和各是多少吗?
名称 四边形 五边形 六边形 n 边形
图形
从一个顶点出发能作的对角线条数
过一个顶点的对角线把多边形分成的三角形个数
多边形内角和
1
2
3
n-3
2
3
4
n-2
2×180°
3×180°
4×180°
(n-2)×180°
一般地,从n边形的一个顶点出发,可以作_________条对角线,它们将n边形分为__________个三角形,n边形的内角和等于______________.
(n - 3)
(n - 2)
(n - 2)×180°
归纳
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
D
C
A
B
解: 如图,在四边形 ABCD 中,
∠A +∠C = 180°,
∵∠A +∠B +∠C +∠D = 360°,
∴ ∠B +∠D = 360° - (∠A +∠C)
= 360° - 180° = 180°
如果一个四边形的一组对角互补,那么另一组对角也互补.
1.一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
解:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
所以这个正多边形是八边形.
针对训练
还有其他解法吗?
解法二:∵正多边形的每一个内角都等于135°,
∴正多边形的每一个外角都等于180°-135°=45°,
由多边形的外角和等于360°
360÷45=8
所以这个正多边形是八边形.
二 多边形的外角和
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少
分析:
1.任意一个外角同它相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角的总和是多少?
互补
6×180°=1080°
解: 六边形的任何一个外角加上与它相邻的内角都等于 180°,因此六边形的 6 个外角加上它们相邻的内角,所得的总和等于 6 × 180°.
这个总和就是六边形的外角和加上内角和,所以外角和等于总和减去内角和,即外角和等于
6 × 180° - ( 6 - 2 ) × 180°= 2 × 180°=360°
思考
如果将例2中六边形换成n边形(n是不小于3的任意整数),可以得到同样结果吗?
n边形外角和
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
n边形的外角和等于360°.
归纳
你知道正多边形的每个内角是多少度吗?每个外角呢?
每个内角的度数是
每个外角的度数是
思考
1. 一个多边形的内角和是 1620°,它是 _________ 边形.
解: 根据多边形的内角和公式,可得 ( n - 2 )·180° = 1620°,
解方程得 n = 11,所以是十一边形.
2. 一个多边形的每一个外角都等于 30°,则这个多边形为 ________ 边形.
解: 由每一个外角都等于 30°,多边形的外角和为 360°,用 360 除以 30 可得这个多边形是十二边形.
十一
十二
针对训练
4. 一个多边形的内角和与外角和相等,它是几边形?
解: 由多边形的内角和与外角和相等,
可得方程为 ( n - 2 )·180° = 360°,解得 n = 4,
所以是四边形.
3.下列角度中,不能成为多边形的内角和的是( )
A.540° B.580° C.1800° D.900°
B
1.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于外角和的2倍,
∴ (n-2) 180°=2× 360 .
解得 n=6.
所以这个多边形的边数为6.
随堂练习
2.一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.
解:设该正多边形的每个内角是 x°,相邻外角是 y°,
则得到一个方程组 解得
而任何多边形的外角和是 360°,
则该正多边形的边数为 360÷120 = 3.
故这个多边形的每个内角的度数是 60°,边数是三条.
外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
多边形的外角和等于360°,与边数无关.
多边形
正多边形
内角= ,外角= .
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十一章 三角形
11.3.2 多边形的内角和
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.经历探索多边形的内角和与外角和公式的过程.
2.学会运用多边形的内角和与外角和公式解决问题.
学习目标
重点
难点
那任意一个
四边形呢?
1.你知道三角形内角和是多少度吗?
三角形内角和等于180°.
长方形和正方形的内角和都是360°.
2.你知道长方形和正方形的内角和是多少度吗?
新课引入
研究多边形的问题通过添加对角线,都可以转化为三角形. 你能利用三角形内角和定理,证明任意一个四边形 ABCD 的内角和等于 360° 吗?
已知:四边形 ABCD,
求证:∠A +∠B +∠C +∠D = 360° .
D
C
A
B
一 多边形内角和
新知学习
已知:四边形 ABCD,
求证:∠A +∠B +∠C +∠D = 360° .
D
C
A
B
方法1
证明:如图,连接 AC,
∠BAD +∠B +∠BCD +∠D
=∠1 +∠2 +∠B +∠3 +∠4 +∠D
=(∠1 +∠3 +∠B) +(∠2 +∠4 +∠D)
= 180°+180° = 360°.
1
2
3
4
方法2
证明:如图,在四边形内部取一点 O,连接 OA,OB,OC,OD,把四边形分成四个三角形.
所以四边形 ABCD 的内角和
= 180°×4 - (∠AOB +∠AOD +∠COD +∠COB)
= 180°×4 - 360°
= 360°.
D
C
A
B
O
方法3
证明:如图,在 BC 边上取一点 O ,连接 OA,OD,把四边形分成三个三角形.
所以四边形 ABCD 的内角和
= 180°×3 - (∠AOB +∠AOD +∠COD )
=180°×3 - 180°
=360°
D
C
A
B
O
方法4
证明:如图,在四边形外任取一点 O,连接 OA,OB,OC,OD,把四边形转化为有一个公共顶点的三个三角形.
所以四边形 ABCD 的内角和
= 180°×3 - (∠COB +∠CBO +∠BCO )
= 180°×3 - 180°
= 360°
D
C
A
B
O
以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为已学的三角形内角和进行求解.
类比上面的过程,你能推导出五边形和六边形的内角和各是多少吗?
名称 四边形 五边形 六边形 n 边形
图形
从一个顶点出发能作的对角线条数
过一个顶点的对角线把多边形分成的三角形个数
多边形内角和
1
2
3
n-3
2
3
4
n-2
2×180°
3×180°
4×180°
(n-2)×180°
一般地,从n边形的一个顶点出发,可以作_________条对角线,它们将n边形分为__________个三角形,n边形的内角和等于______________.
(n - 3)
(n - 2)
(n - 2)×180°
归纳
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
D
C
A
B
解: 如图,在四边形 ABCD 中,
∠A +∠C = 180°,
∵∠A +∠B +∠C +∠D = 360°,
∴ ∠B +∠D = 360° - (∠A +∠C)
= 360° - 180° = 180°
如果一个四边形的一组对角互补,那么另一组对角也互补.
1.一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
解:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
所以这个正多边形是八边形.
针对训练
还有其他解法吗?
解法二:∵正多边形的每一个内角都等于135°,
∴正多边形的每一个外角都等于180°-135°=45°,
由多边形的外角和等于360°
360÷45=8
所以这个正多边形是八边形.
二 多边形的外角和
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少
分析:
1.任意一个外角同它相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角的总和是多少?
互补
6×180°=1080°
解: 六边形的任何一个外角加上与它相邻的内角都等于 180°,因此六边形的 6 个外角加上它们相邻的内角,所得的总和等于 6 × 180°.
这个总和就是六边形的外角和加上内角和,所以外角和等于总和减去内角和,即外角和等于
6 × 180° - ( 6 - 2 ) × 180°= 2 × 180°=360°
思考
如果将例2中六边形换成n边形(n是不小于3的任意整数),可以得到同样结果吗?
n边形外角和
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
n边形的外角和等于360°.
归纳
你知道正多边形的每个内角是多少度吗?每个外角呢?
每个内角的度数是
每个外角的度数是
思考
1. 一个多边形的内角和是 1620°,它是 _________ 边形.
解: 根据多边形的内角和公式,可得 ( n - 2 )·180° = 1620°,
解方程得 n = 11,所以是十一边形.
2. 一个多边形的每一个外角都等于 30°,则这个多边形为 ________ 边形.
解: 由每一个外角都等于 30°,多边形的外角和为 360°,用 360 除以 30 可得这个多边形是十二边形.
十一
十二
针对训练
4. 一个多边形的内角和与外角和相等,它是几边形?
解: 由多边形的内角和与外角和相等,
可得方程为 ( n - 2 )·180° = 360°,解得 n = 4,
所以是四边形.
3.下列角度中,不能成为多边形的内角和的是( )
A.540° B.580° C.1800° D.900°
B
1.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于外角和的2倍,
∴ (n-2) 180°=2× 360 .
解得 n=6.
所以这个多边形的边数为6.
随堂练习
2.一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.
解:设该正多边形的每个内角是 x°,相邻外角是 y°,
则得到一个方程组 解得
而任何多边形的外角和是 360°,
则该正多边形的边数为 360÷120 = 3.
故这个多边形的每个内角的度数是 60°,边数是三条.
外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
多边形的外角和等于360°,与边数无关.
多边形
正多边形
内角= ,外角= .
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
