22.1.2二次函数y=ax2的图象和性质(第1课时) 课件(32张PPT)
文档属性
| 名称 | 22.1.2二次函数y=ax2的图象和性质(第1课时) 课件(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 42.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 15:05:21 | ||
图片预览


文档简介
(共32张PPT)
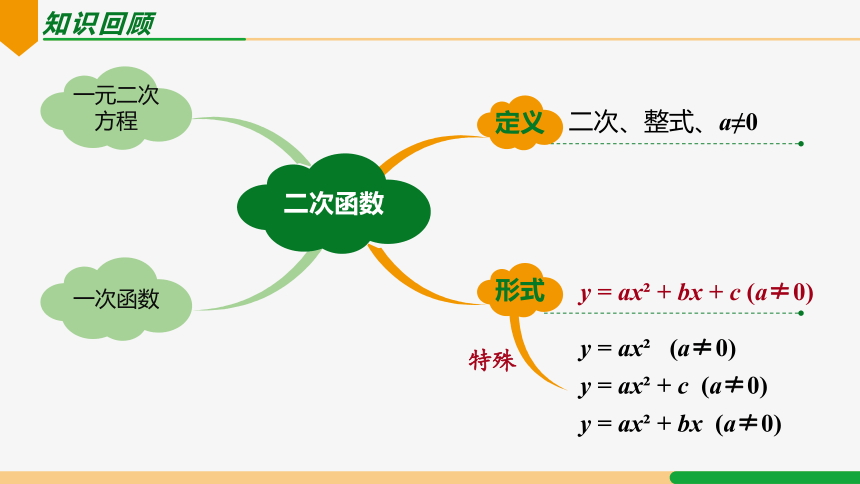
y=ax 的图象和性质
22.1.2 二次函数y=ax 的图象和性质
| 第1课时|
课堂导航
学习二次函数的基本思路和方法
y=ax 的图象和性质
二次、整式、a≠0
y = ax + bx + c (a≠0)
知识回顾
y = ax (a≠0)
y = ax + c (a≠0)
y = ax + bx (a≠0)
特殊
一元二次
方程
一次函数
定义
形式
二次函数
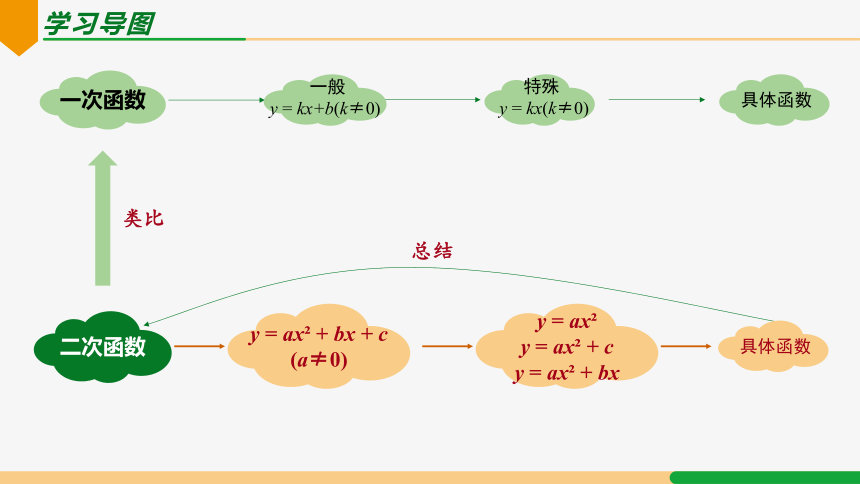
学习导图
类比
特殊
y = kx(k≠0)
一次函数
一般
y = kx+b(k≠0)
具体函数
二次函数
y = ax + bx + c
(a≠0)
y = ax
y = ax + c
y = ax + bx
具体函数
总结
新知探究
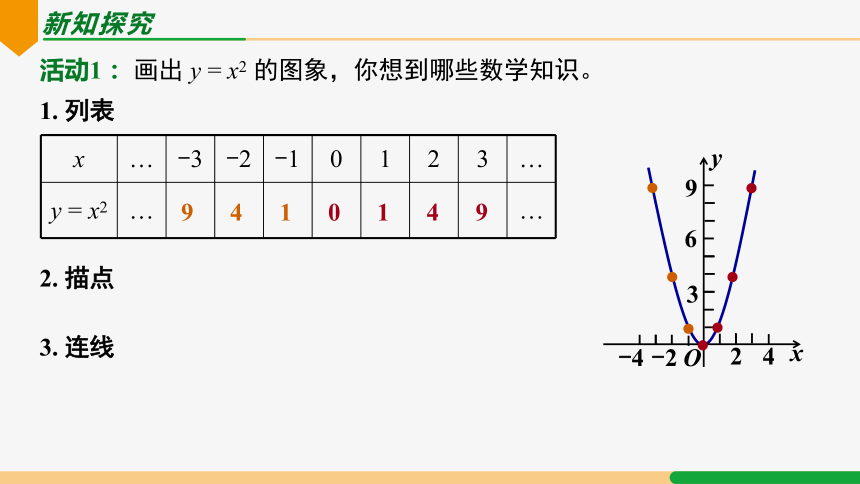
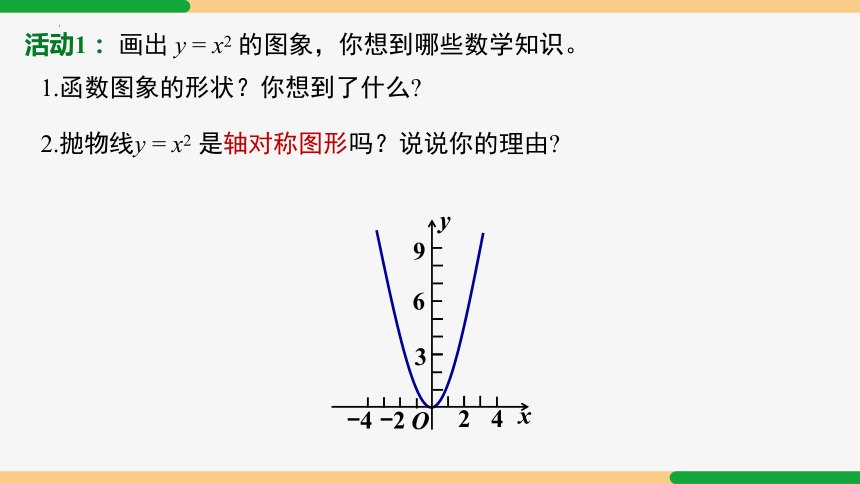
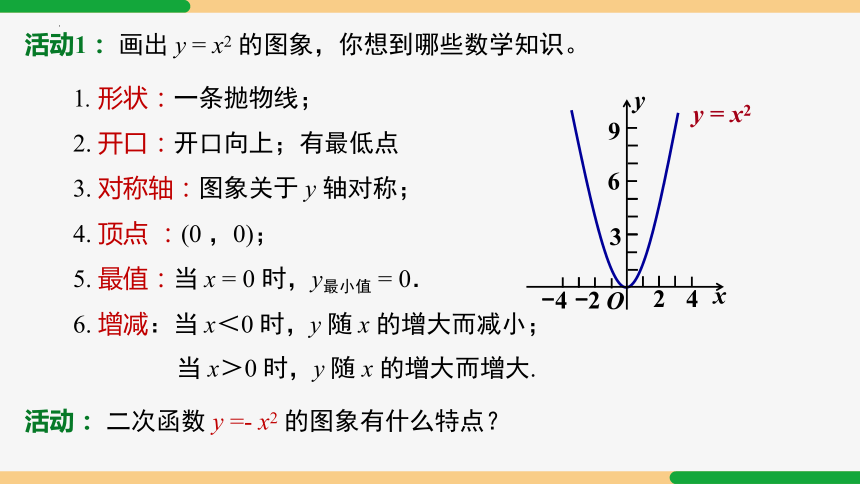
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
x … -3 -2 -1 0 1 2 3 …
y = x2 … …
9
4
1
0
1
9
4
1. 列表
2. 描点
3. 连线
2
4
-2
-4
O
3
6
9
x
y
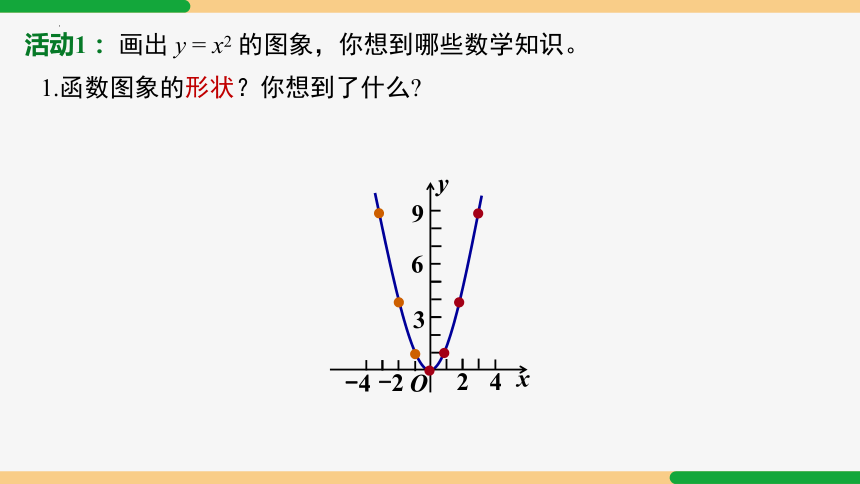
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
2
4
-2
-4
O
3
6
9
x
y
1.函数图象的形状?你想到了什么
知识要点1
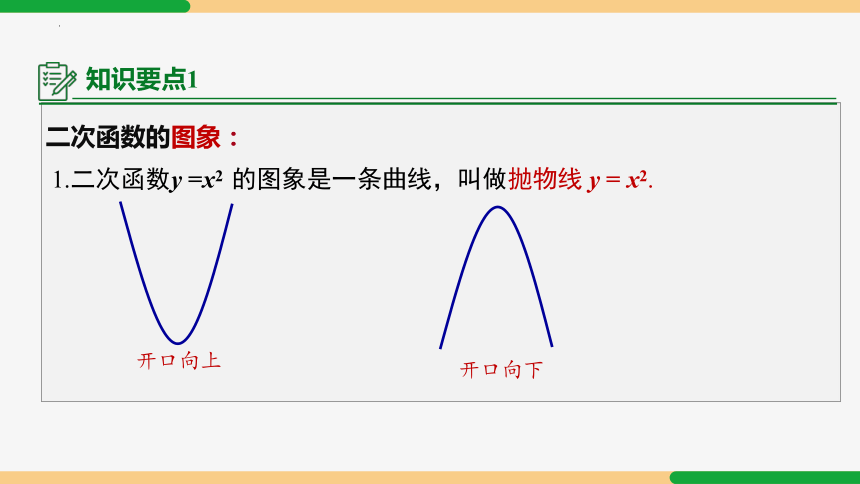
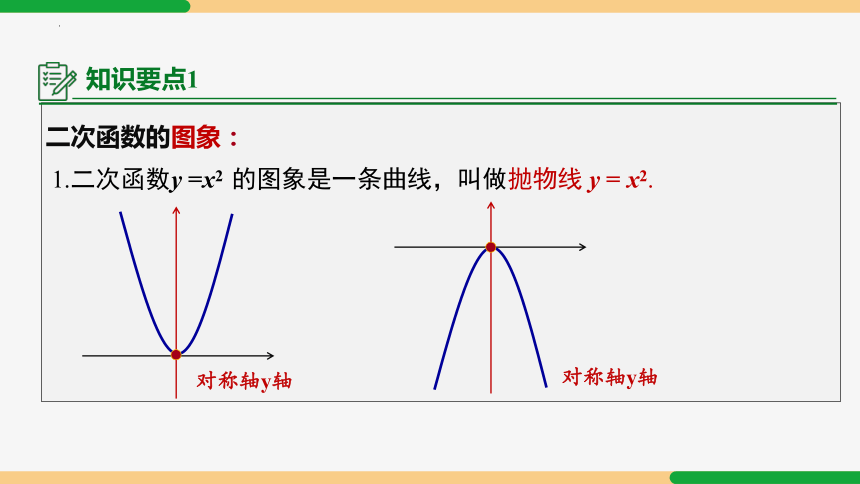
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
开口向上
开口向下
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
1.函数图象的形状?你想到了什么
2.抛物线y = x2 是轴对称图形吗?说说你的理由
2
4
-2
-4
O
3
6
9
x
y
知识要点1
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
对称轴y轴
对称轴y轴
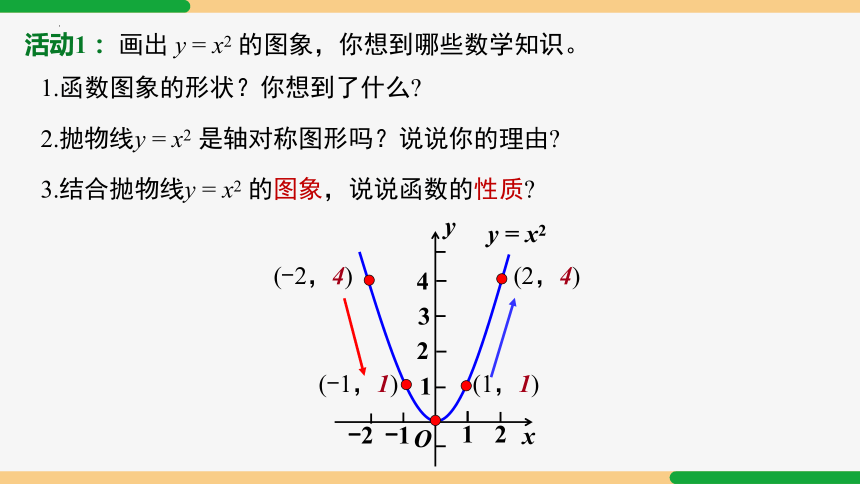
(-2,4)
(-1,1)
(2,4)
(1,1)
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
1.函数图象的形状?你想到了什么
2.抛物线y = x2 是轴对称图形吗?说说你的理由
3.结合抛物线y = x2 的图象,说说函数的性质
1
2
-2
O
-1
1
4
x
y
3
2
y = x2
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
2
4
-2
-4
O
3
6
9
x
y
y = x2
1. 形状:一条抛物线;
2. 开口:开口向上;有最低点
3. 对称轴:图象关于 y 轴对称;
4. 顶点 :(0 ,0);
5. 最值:当 x = 0 时,y最小值 = 0.
6. 增减:当 x<0 时,y 随 x 的增大而减小; 当 x>0 时,y 随 x 的增大而增大.
活动: 二次函数 y =- x2 的图象有什么特点?
x … -3 -2 -1 0 1 2 3 …
y = -x2 … …
-9
-4
-1
0
-1
-9
-4
1. 列表
2. 描点
3. 连线
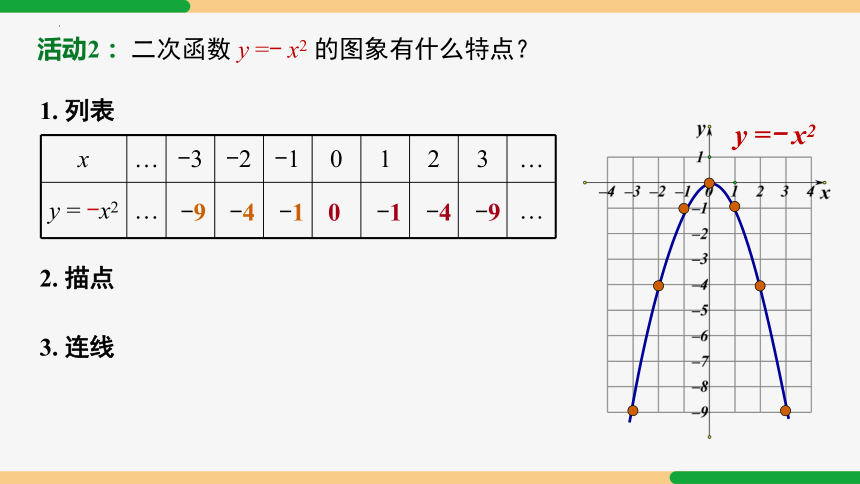
活动2: 二次函数 y =- x2 的图象有什么特点?
y =- x2
活动2: 二次函数 y =- x2 的图象有什么特点?
y =- x2
1. 形状:一条抛物线;
2. 开口:开口向下;有最高点
3. 对称轴:图象关于 y 轴对称;
4. 顶点 :(0 ,0);
5. 最值:当 x = 0 时,y最大值 = 0.
6. 增减:当 x<0 时,y 随 x 的增大而增大; 当 x>0 时,y 随 x 的增大而减小.
活动3: 在同一直角坐标系中,画出函数y =x2和 y = - x2 的草图
1.两个图象有什么相同点和不同点?
2.两个图象可以怎样变换得到?
y = x2
y =- x2
x
y
o
知识要点2
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
a>0
2.二次函数y =ax2 中的a符号决定抛物线的开口方向
a<0
典例讲解
例1 在同一直角坐标系中,画出函数 的图象.
x ··· 4 3 2 1 0 1 2 3 4 ···
··· ···
8
2
0.5
0
8
4.5
2
0.5
4.5
1.列表
x ··· 2 1.5 1 0.5 0 0.5 1 1.5 2 ···
y=2x2 ··· ···
8
2
0.5
0
8
4.5
2
0.5
4.5
例1 在同一直角坐标系中,画出函数 的图象.
O
-2
2
2
4
6
4
-4
8
x
y
y = 2x2
思考
1.两个图象有什么相同点和不同点?
2.你从中归纳总结规律?
y = x2
知识要点3
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
a>0
2.二次函数y =ax2 中的a符号决定抛物线的开口方向
a<0
知识要点3
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
2.二次函数y =ax2 中的a符号决定抛物线的开口方向
3.二次函数y =ax2 中的a大小决定抛物线的开口大小
O
x
y
y = 2x2
y = x2
O
x
y
y = 2x2
y = x2
y=ax2 a > 0
开口
对称轴
顶点
最值
增减性
开口向上
关于 y 轴对称,对称轴是直线 x=0
原点(0,0)
当 x = 0 时,y最小值 = 0
当 x < 0 时,y 随 x 增大而减小;
当 x > 0 时,y 随 x 增大而增大.
针对练习
1. 画出函数 y = 4x2 的图象的划图,填空
(1)开口 ,对称轴是 ,
(2)顶点是 ,顶点是抛物线的最 点;
(3)在对称轴的左侧,y 随 x 的增大而 ,
在对称轴的右侧,y 随 x 的增大而 ;
(4)点 A(2,y1) 在抛物线上,则 y1 = ________.
(5)点 A(2,16) 关于对称轴的对称点的坐标是_________.
向上
y 轴
(0,0)
低
减小
增大
( 2,16)
16
x ··· 4 3 2 1 0 1 2 3 4 ···
··· ···
y=-x2 ··· ···
例2 在同一直角坐标系中,画出函数 观察图象, (1)这些抛物线有什么相同点和不同点?
(2)你从中归纳总结规律?
8
2
0.5
0
8
4.5
2
0.5
4.5
1.列表
x ··· 2 1.5 1 0.5 0 0.5 1 1.5 2 ···
y=-2x2 ··· ···
9
4
1
0
1
9
4
16
16
8
2
0.5
0
8
4.5
2
0.5
4.5
例2 在同一直角坐标系中,画出函数 观察图象, (1)这些抛物线有什么相同点和不同点?
(2)你从中归纳总结规律?
2.描点
2
2
-2
-4
-6
4
4
-8
x
y
y = -2x2
O
3.连线
例2 在同一直角坐标系中,画出函数 观察图象,
2
2
-2
-4
-6
4
4
-8
x
y
y = -2x2
O
y=ax2 a < 0
开口
对称轴
顶点
最值
增减性
开口向上
关于 y 轴对称,对称轴是直线 x=0
原点(0,0)
当 x = 0 时,y最大值 = 0
当 x < 0 时,y 随 x 增大而增大;
当 x > 0 时,y 随 x 增大而减小
例3 在同一直角坐标系中,画出下列函数的草图,总结a对图象的作用。
(1) y=x2 (2)
y = 2x2
y = x2
y = -2x2
2
2
-2
-4
-6
4
4
-8
x
y
O
O
-2
2
2
4
6
4
-4
8
x
y
知识要点3
二次函数的图象:
3.二次函数y =ax2 中的a决定抛物线的开口
(1) a符号决定抛物线的开口方向,正上负下
(2) a绝对值决定抛物线的大小,|a|越大,开口越小
知识要点
y=ax2 a > 0 a < 0
图象
开口
对称轴
顶点
最值
增减性
开口向上,a 越大,开口越小
y 轴(直线 x=0)
原点(0,0)
当 x = 0 时,y最小值 = 0
当 x < 0 时,y 随 x 增大而减小;
当 x > 0 时,y 随 x 增大而增大.
开口向下,a 越大,开口越大
y 轴(直线 x=0)
原点(0,0)
当 x = 0 时,y最小值 = 0
当 x < 0 时,y 随 x 增大而减小;
当 x > 0 时,y 随 x 增大而增大.
x
y
x
y
针对练习
3. 函数 y = x2 的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;
2. 函数 y = 3x2 的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;
1. 函数 y = 4x2 的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y 轴
y 轴
(0,0)
(0,0)
4. 函数 y = 0.2x2 的图象的开口 ,对称轴是____,顶点是 .
向上
y 轴
(0,0)
向下
y 轴
(0,0)
高
低
a >0
课堂小结
图象
一次函数
二次函数
x
y
x
y
a <0
抛物线开口
抛物线对称轴
抛物线顶点
函数的最值
函数的增减
性质
y=ax2(a≠0)
类比
特例
a
课堂练习
1. 如右图,观察函数 y = (k - 1)x2 的图象,则 k 的取值范围是 .
k > 1
2. 说出下列抛物线的开口方向、对称轴和顶点.
开口方向
对称轴
顶点
向上
向下
向下
向上
y 轴
y 轴
y 轴
y 轴
(0,0)
(0,0)
(0,0)
(0,0)
x
y
O
二次函数
3.函数y=2x2的图象的开口 , 对称轴 ,顶点是 ; 在对称轴的左侧,y随x的增大而 , 在对称轴的右侧, y随x的增大而 .
4.函数y=-3x2的图象的开口 , 对称轴 ,顶点是 ; 在对称轴的左侧, y随x的增大而 , 在对称轴的右侧, y随x的增大而 .
向上
向下
y轴
y轴
(0,0)
(0,0)
减小
减小
增大
增大
5.已知二次函数 y=ax2.
(1) 若 a = 2,点( 2,y1)与(3,y2)在此二次函数的图象上, 则 y1_____ y2
<
(2) 若 a>0,点(2,y1)与(3,y2)在此二次函数的图象上, 则 y1_____ y2
(3) 若 a<0,点(-2,y1)与(3,y2),(5,y3)在此二次函数 的图象上,则y1,y2,y3的大小关系是___________.
<
y1>y2>y3
y=ax 的图象和性质
22.1.2 二次函数y=ax 的图象和性质
| 第1课时|
课堂导航
学习二次函数的基本思路和方法
y=ax 的图象和性质
二次、整式、a≠0
y = ax + bx + c (a≠0)
知识回顾
y = ax (a≠0)
y = ax + c (a≠0)
y = ax + bx (a≠0)
特殊
一元二次
方程
一次函数
定义
形式
二次函数
学习导图
类比
特殊
y = kx(k≠0)
一次函数
一般
y = kx+b(k≠0)
具体函数
二次函数
y = ax + bx + c
(a≠0)
y = ax
y = ax + c
y = ax + bx
具体函数
总结
新知探究
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
x … -3 -2 -1 0 1 2 3 …
y = x2 … …
9
4
1
0
1
9
4
1. 列表
2. 描点
3. 连线
2
4
-2
-4
O
3
6
9
x
y
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
2
4
-2
-4
O
3
6
9
x
y
1.函数图象的形状?你想到了什么
知识要点1
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
开口向上
开口向下
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
1.函数图象的形状?你想到了什么
2.抛物线y = x2 是轴对称图形吗?说说你的理由
2
4
-2
-4
O
3
6
9
x
y
知识要点1
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
对称轴y轴
对称轴y轴
(-2,4)
(-1,1)
(2,4)
(1,1)
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
1.函数图象的形状?你想到了什么
2.抛物线y = x2 是轴对称图形吗?说说你的理由
3.结合抛物线y = x2 的图象,说说函数的性质
1
2
-2
O
-1
1
4
x
y
3
2
y = x2
活动1: 画出 y = x2 的图象,你想到哪些数学知识。
2
4
-2
-4
O
3
6
9
x
y
y = x2
1. 形状:一条抛物线;
2. 开口:开口向上;有最低点
3. 对称轴:图象关于 y 轴对称;
4. 顶点 :(0 ,0);
5. 最值:当 x = 0 时,y最小值 = 0.
6. 增减:当 x<0 时,y 随 x 的增大而减小; 当 x>0 时,y 随 x 的增大而增大.
活动: 二次函数 y =- x2 的图象有什么特点?
x … -3 -2 -1 0 1 2 3 …
y = -x2 … …
-9
-4
-1
0
-1
-9
-4
1. 列表
2. 描点
3. 连线
活动2: 二次函数 y =- x2 的图象有什么特点?
y =- x2
活动2: 二次函数 y =- x2 的图象有什么特点?
y =- x2
1. 形状:一条抛物线;
2. 开口:开口向下;有最高点
3. 对称轴:图象关于 y 轴对称;
4. 顶点 :(0 ,0);
5. 最值:当 x = 0 时,y最大值 = 0.
6. 增减:当 x<0 时,y 随 x 的增大而增大; 当 x>0 时,y 随 x 的增大而减小.
活动3: 在同一直角坐标系中,画出函数y =x2和 y = - x2 的草图
1.两个图象有什么相同点和不同点?
2.两个图象可以怎样变换得到?
y = x2
y =- x2
x
y
o
知识要点2
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
a>0
2.二次函数y =ax2 中的a符号决定抛物线的开口方向
a<0
典例讲解
例1 在同一直角坐标系中,画出函数 的图象.
x ··· 4 3 2 1 0 1 2 3 4 ···
··· ···
8
2
0.5
0
8
4.5
2
0.5
4.5
1.列表
x ··· 2 1.5 1 0.5 0 0.5 1 1.5 2 ···
y=2x2 ··· ···
8
2
0.5
0
8
4.5
2
0.5
4.5
例1 在同一直角坐标系中,画出函数 的图象.
O
-2
2
2
4
6
4
-4
8
x
y
y = 2x2
思考
1.两个图象有什么相同点和不同点?
2.你从中归纳总结规律?
y = x2
知识要点3
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
a>0
2.二次函数y =ax2 中的a符号决定抛物线的开口方向
a<0
知识要点3
二次函数的图象:
1.二次函数y =x2 的图象是一条曲线,叫做抛物线 y = x2.
2.二次函数y =ax2 中的a符号决定抛物线的开口方向
3.二次函数y =ax2 中的a大小决定抛物线的开口大小
O
x
y
y = 2x2
y = x2
O
x
y
y = 2x2
y = x2
y=ax2 a > 0
开口
对称轴
顶点
最值
增减性
开口向上
关于 y 轴对称,对称轴是直线 x=0
原点(0,0)
当 x = 0 时,y最小值 = 0
当 x < 0 时,y 随 x 增大而减小;
当 x > 0 时,y 随 x 增大而增大.
针对练习
1. 画出函数 y = 4x2 的图象的划图,填空
(1)开口 ,对称轴是 ,
(2)顶点是 ,顶点是抛物线的最 点;
(3)在对称轴的左侧,y 随 x 的增大而 ,
在对称轴的右侧,y 随 x 的增大而 ;
(4)点 A(2,y1) 在抛物线上,则 y1 = ________.
(5)点 A(2,16) 关于对称轴的对称点的坐标是_________.
向上
y 轴
(0,0)
低
减小
增大
( 2,16)
16
x ··· 4 3 2 1 0 1 2 3 4 ···
··· ···
y=-x2 ··· ···
例2 在同一直角坐标系中,画出函数 观察图象, (1)这些抛物线有什么相同点和不同点?
(2)你从中归纳总结规律?
8
2
0.5
0
8
4.5
2
0.5
4.5
1.列表
x ··· 2 1.5 1 0.5 0 0.5 1 1.5 2 ···
y=-2x2 ··· ···
9
4
1
0
1
9
4
16
16
8
2
0.5
0
8
4.5
2
0.5
4.5
例2 在同一直角坐标系中,画出函数 观察图象, (1)这些抛物线有什么相同点和不同点?
(2)你从中归纳总结规律?
2.描点
2
2
-2
-4
-6
4
4
-8
x
y
y = -2x2
O
3.连线
例2 在同一直角坐标系中,画出函数 观察图象,
2
2
-2
-4
-6
4
4
-8
x
y
y = -2x2
O
y=ax2 a < 0
开口
对称轴
顶点
最值
增减性
开口向上
关于 y 轴对称,对称轴是直线 x=0
原点(0,0)
当 x = 0 时,y最大值 = 0
当 x < 0 时,y 随 x 增大而增大;
当 x > 0 时,y 随 x 增大而减小
例3 在同一直角坐标系中,画出下列函数的草图,总结a对图象的作用。
(1) y=x2 (2)
y = 2x2
y = x2
y = -2x2
2
2
-2
-4
-6
4
4
-8
x
y
O
O
-2
2
2
4
6
4
-4
8
x
y
知识要点3
二次函数的图象:
3.二次函数y =ax2 中的a决定抛物线的开口
(1) a符号决定抛物线的开口方向,正上负下
(2) a绝对值决定抛物线的大小,|a|越大,开口越小
知识要点
y=ax2 a > 0 a < 0
图象
开口
对称轴
顶点
最值
增减性
开口向上,a 越大,开口越小
y 轴(直线 x=0)
原点(0,0)
当 x = 0 时,y最小值 = 0
当 x < 0 时,y 随 x 增大而减小;
当 x > 0 时,y 随 x 增大而增大.
开口向下,a 越大,开口越大
y 轴(直线 x=0)
原点(0,0)
当 x = 0 时,y最小值 = 0
当 x < 0 时,y 随 x 增大而减小;
当 x > 0 时,y 随 x 增大而增大.
x
y
x
y
针对练习
3. 函数 y = x2 的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;
2. 函数 y = 3x2 的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;
1. 函数 y = 4x2 的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y 轴
y 轴
(0,0)
(0,0)
4. 函数 y = 0.2x2 的图象的开口 ,对称轴是____,顶点是 .
向上
y 轴
(0,0)
向下
y 轴
(0,0)
高
低
a >0
课堂小结
图象
一次函数
二次函数
x
y
x
y
a <0
抛物线开口
抛物线对称轴
抛物线顶点
函数的最值
函数的增减
性质
y=ax2(a≠0)
类比
特例
a
课堂练习
1. 如右图,观察函数 y = (k - 1)x2 的图象,则 k 的取值范围是 .
k > 1
2. 说出下列抛物线的开口方向、对称轴和顶点.
开口方向
对称轴
顶点
向上
向下
向下
向上
y 轴
y 轴
y 轴
y 轴
(0,0)
(0,0)
(0,0)
(0,0)
x
y
O
二次函数
3.函数y=2x2的图象的开口 , 对称轴 ,顶点是 ; 在对称轴的左侧,y随x的增大而 , 在对称轴的右侧, y随x的增大而 .
4.函数y=-3x2的图象的开口 , 对称轴 ,顶点是 ; 在对称轴的左侧, y随x的增大而 , 在对称轴的右侧, y随x的增大而 .
向上
向下
y轴
y轴
(0,0)
(0,0)
减小
减小
增大
增大
5.已知二次函数 y=ax2.
(1) 若 a = 2,点( 2,y1)与(3,y2)在此二次函数的图象上, 则 y1_____ y2
<
(2) 若 a>0,点(2,y1)与(3,y2)在此二次函数的图象上, 则 y1_____ y2
(3) 若 a<0,点(-2,y1)与(3,y2),(5,y3)在此二次函数 的图象上,则y1,y2,y3的大小关系是___________.
<
y1>y2>y3
同课章节目录
