图形的全等
图片预览

文档简介
§15.4 图形的全等
教学目标
知识与技能:理解全等图形的概念,认识全等图形在通过一系列变换之后两个图形能够完全重合.
过程与方法:经历探究图形全等的过程,掌握全等图形(多边形、三角形)的特征.
情感态度与价值观:以积极的态度进行合作学习,形成良好的几何认知,体会全等图形的实际应用价值.
重点、难点、关键
重点:认识图形的全等,领会其特征.
难点:对全等图形的识别.
关键:以观察、实践的思想意识来探索几何图形,认知图形特征.
教学准备
教师准备:投影片、直尺、图片.
学生准备:寻找一些全等图形的生活图片.
教学过程
一、创设情境
投影显示
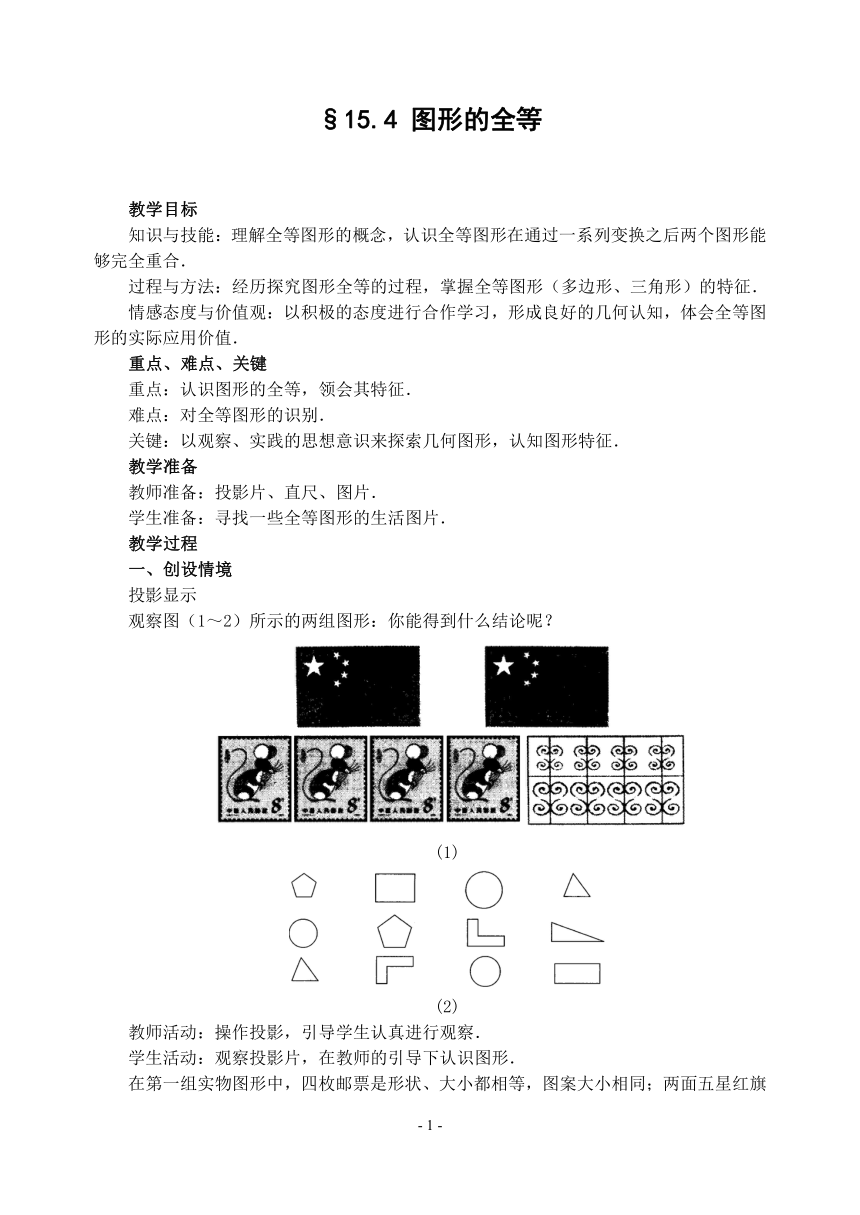
观察图(1~2)所示的两组图形:你能得到什么结论呢?
(1)
(2)
教师活动:操作投影,引导学生认真进行观察.
学生活动:观察投影片,在教师的引导下认识图形.
在第一组实物图形中,四枚邮票是形状、大小都相等,图案大小相同;两面五星红旗也有此特征;铁栅栏中的大小“S”分别是大小、形状都相同.第二组几何图形中的两个小圆,两个小“L”形,两个三角形形状、大小都一样,也就是说通过翻折、平移和旋转变换,几个图形会完全叠合在一起.
教师定义:能够完全重合的两个图形叫做全等图形.
媒体使用:教师把收集来的全等图形以及学生收集来的全等图形通过投影仪(实物)让学生欣赏,识别,加深概念.(也可以直接拿给学生看)
二、阅读与思考
1.阅读课本P85第1~12行内容.
评析:目的是让学生通过观察,对图形全等有感性认识.
2.思考课本P85问题.
观察课本图15.4.2中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
教师活动:引导学生分析两对多边形,让学生明确它们都是全等图形,称为全等多边形,讲明对应顶点、对应边、对应角的概念.
3.议一议:
(1)你能说出生活中全等图形的例子吗?
(2)观察下面两组图形,它们是不是全等图形?为什么?
(3)如果两个图形全等,它们的形状和大小一定都相同吗?
评析:使学生认识全等图形的特征,按照是否重合可以判断出这两组图形都不全等,进一步让学生发现图(a)中的两个图形形状相同,但大小不同;图(b)中的两个图形面积相同,但形状不同.
三、继续探究
1.引入全等图形的表示法:
如课本图15.4.3这两个图形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′,符号“≌”表示全等,读作“全等于”,点A与A′,点B与B′,点C与C′,点D与D′,点E与E′分别是对应提出.
教师活动:介绍全等多边形,引入全等多边形性质:全等多边形的对应边、对应角分别相等.这一全等多边形特征.再进一步说明识别两个多边形全等的方法是,对应边、对应角分别相等的两个多边形全等.
学生活动:观察,接受全等多边形的性质与判定,并进行理解.
教师活动:操作投影仪显示课本图15.4.4,介绍特殊多边形──三角形,指出全等三角形的对应边、对应角分别相等,反之可做为判断两个三角形全等的条件.
学生活动:观察从一般到特殊,突出三角形全等性质和判别.
四、随堂练习
课本P87练习.
探研时空.
1.做一做:
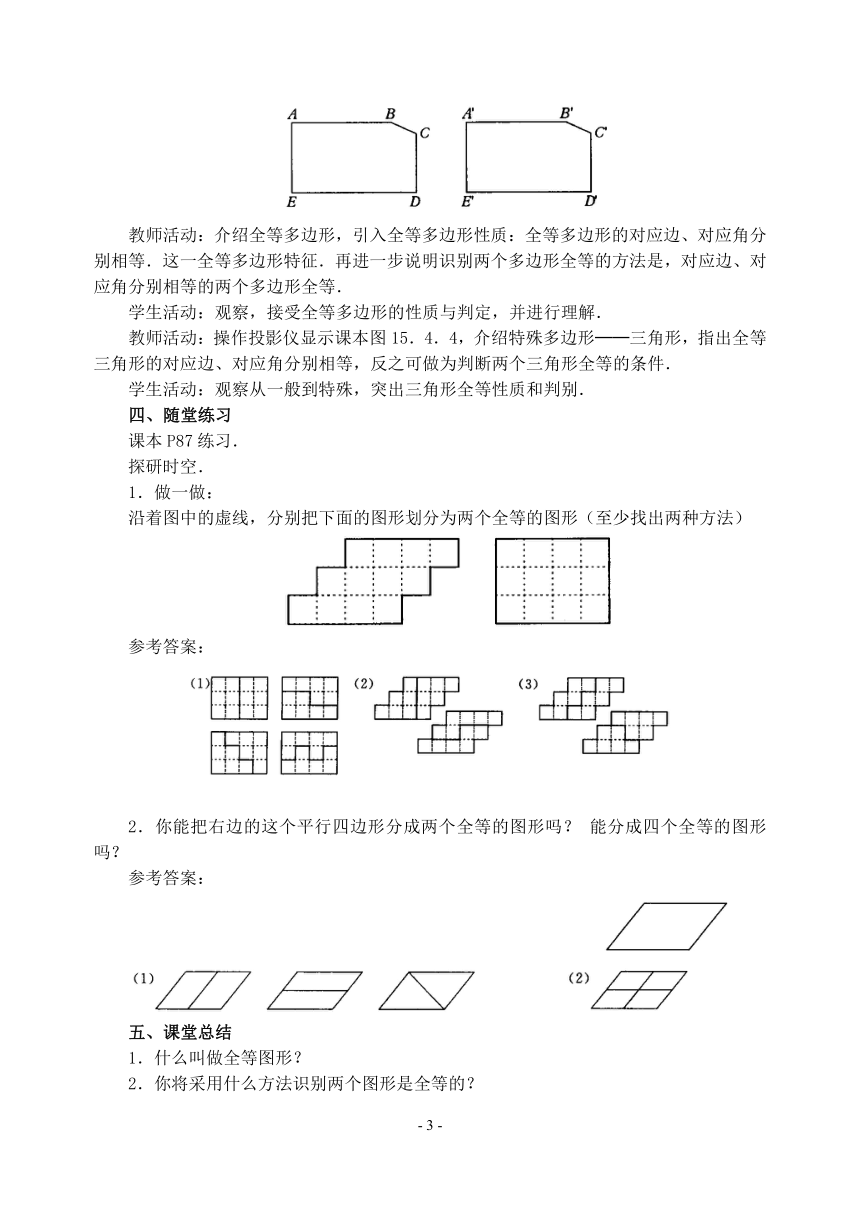
沿着图中的虚线,分别把下面的图形划分为两个全等的图形(至少找出两种方法)
参考答案:
2.你能把右边的这个平行四边形分成两个全等的图形吗?能分成四个全等的图形吗?
参考答案:
五、课堂总结
1.什么叫做全等图形?
2.你将采用什么方法识别两个图形是全等的?
3.全等三角形具有哪些性质?你是怎样识别两个三角形全等的?
4.这节课对你认知平移、旋转有何帮助?
六、布置作业
1.课本P87习题15.4第1,2题.
2.选用课时作业设计.
七、课后反思(略)
课时作业设计
1.如图所示,做四个全等的小“L”型纸片,将它们拼成与大“L”型全等的图案.
2.如图(a~l)所示,下面图形中有哪些是全等的?
3.如图所示,观察下面图案,你能发现其中的全等图形吗?
4.在图(a~b)中找出两对全等的三角形,并指出其中的对应角和对应边.
5.找出七巧板拼成的图案中的全等三角形.
6.如图所示,△ABC≌△AEC,∠B=30°,∠ACB=85°,求出△AEC各内角的度数.
7.如图所示,是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?
8.如图所示,△AOD≌△BOC,写出其中相等的角.
9.如图所示,△ABC≌△A′B′C′,∠C=25°,BC=6cm,AC=4cm,你能得出△A′B′C′中哪些角的大小,哪些边的长度?
10.如图所示,一栅栏顶部是由全等的三角形组成的,其中,AC=0.2m,BC=2AC,求BD的长.
参考答案
1.
2.a与h,b与l,d与i,e与k 3~5.略
6.∠AEC=30° ∠EAC=65° ∠ECA=85°
7.
8.∠D=∠C ∠A=∠B ∠DOA=∠COB
9.∠C′=25° B′C′=6cm A′C′=4cm
10.BD=7BC=14AC=2.8m
- 1 -
教学目标
知识与技能:理解全等图形的概念,认识全等图形在通过一系列变换之后两个图形能够完全重合.
过程与方法:经历探究图形全等的过程,掌握全等图形(多边形、三角形)的特征.
情感态度与价值观:以积极的态度进行合作学习,形成良好的几何认知,体会全等图形的实际应用价值.
重点、难点、关键
重点:认识图形的全等,领会其特征.
难点:对全等图形的识别.
关键:以观察、实践的思想意识来探索几何图形,认知图形特征.
教学准备
教师准备:投影片、直尺、图片.
学生准备:寻找一些全等图形的生活图片.
教学过程
一、创设情境
投影显示
观察图(1~2)所示的两组图形:你能得到什么结论呢?
(1)
(2)
教师活动:操作投影,引导学生认真进行观察.
学生活动:观察投影片,在教师的引导下认识图形.
在第一组实物图形中,四枚邮票是形状、大小都相等,图案大小相同;两面五星红旗也有此特征;铁栅栏中的大小“S”分别是大小、形状都相同.第二组几何图形中的两个小圆,两个小“L”形,两个三角形形状、大小都一样,也就是说通过翻折、平移和旋转变换,几个图形会完全叠合在一起.
教师定义:能够完全重合的两个图形叫做全等图形.
媒体使用:教师把收集来的全等图形以及学生收集来的全等图形通过投影仪(实物)让学生欣赏,识别,加深概念.(也可以直接拿给学生看)
二、阅读与思考
1.阅读课本P85第1~12行内容.
评析:目的是让学生通过观察,对图形全等有感性认识.
2.思考课本P85问题.
观察课本图15.4.2中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
教师活动:引导学生分析两对多边形,让学生明确它们都是全等图形,称为全等多边形,讲明对应顶点、对应边、对应角的概念.
3.议一议:
(1)你能说出生活中全等图形的例子吗?
(2)观察下面两组图形,它们是不是全等图形?为什么?
(3)如果两个图形全等,它们的形状和大小一定都相同吗?
评析:使学生认识全等图形的特征,按照是否重合可以判断出这两组图形都不全等,进一步让学生发现图(a)中的两个图形形状相同,但大小不同;图(b)中的两个图形面积相同,但形状不同.
三、继续探究
1.引入全等图形的表示法:
如课本图15.4.3这两个图形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′,符号“≌”表示全等,读作“全等于”,点A与A′,点B与B′,点C与C′,点D与D′,点E与E′分别是对应提出.
教师活动:介绍全等多边形,引入全等多边形性质:全等多边形的对应边、对应角分别相等.这一全等多边形特征.再进一步说明识别两个多边形全等的方法是,对应边、对应角分别相等的两个多边形全等.
学生活动:观察,接受全等多边形的性质与判定,并进行理解.
教师活动:操作投影仪显示课本图15.4.4,介绍特殊多边形──三角形,指出全等三角形的对应边、对应角分别相等,反之可做为判断两个三角形全等的条件.
学生活动:观察从一般到特殊,突出三角形全等性质和判别.
四、随堂练习
课本P87练习.
探研时空.
1.做一做:
沿着图中的虚线,分别把下面的图形划分为两个全等的图形(至少找出两种方法)
参考答案:
2.你能把右边的这个平行四边形分成两个全等的图形吗?能分成四个全等的图形吗?
参考答案:
五、课堂总结
1.什么叫做全等图形?
2.你将采用什么方法识别两个图形是全等的?
3.全等三角形具有哪些性质?你是怎样识别两个三角形全等的?
4.这节课对你认知平移、旋转有何帮助?
六、布置作业
1.课本P87习题15.4第1,2题.
2.选用课时作业设计.
七、课后反思(略)
课时作业设计
1.如图所示,做四个全等的小“L”型纸片,将它们拼成与大“L”型全等的图案.
2.如图(a~l)所示,下面图形中有哪些是全等的?
3.如图所示,观察下面图案,你能发现其中的全等图形吗?
4.在图(a~b)中找出两对全等的三角形,并指出其中的对应角和对应边.
5.找出七巧板拼成的图案中的全等三角形.
6.如图所示,△ABC≌△AEC,∠B=30°,∠ACB=85°,求出△AEC各内角的度数.
7.如图所示,是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?
8.如图所示,△AOD≌△BOC,写出其中相等的角.
9.如图所示,△ABC≌△A′B′C′,∠C=25°,BC=6cm,AC=4cm,你能得出△A′B′C′中哪些角的大小,哪些边的长度?
10.如图所示,一栅栏顶部是由全等的三角形组成的,其中,AC=0.2m,BC=2AC,求BD的长.
参考答案
1.
2.a与h,b与l,d与i,e与k 3~5.略
6.∠AEC=30° ∠EAC=65° ∠ECA=85°
7.
8.∠D=∠C ∠A=∠B ∠DOA=∠COB
9.∠C′=25° B′C′=6cm A′C′=4cm
10.BD=7BC=14AC=2.8m
- 1 -
