算法案例(第一课时)
图片预览






文档简介
(共15张PPT)
算法案例
1. 回顾算法的三种表述:
自然语言
程序框图
程序语言
(三种逻辑结构)
(五种基本语句)
2. 思考:
小学学过的求两个数最大公约数的方法?
先用两个公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来.
1、求两个正整数的最大公约数
(1)求25和35的最大公约数
(2)求18和30的最大公约数
25
(1)
5
5
35
7
18
(2)
2
9
30
15
所以,25和35的最大公约数为5
所以,18和30的最大公约数为6
2、除了用这种方法外还有没有其它方法?
算出8256和6105的最大公约数.
3
3
5
辗转相除法(欧几里得算法)
观察用辗转相除法求8251和6105的最大公约数的过程
第一步 用两数中较大的数除以较小的数,求得商和余数 8251=6105×1+2146
结论: 8251和6105的公约数就是6105和2146的公约数,反之也成立。求8251和6105的最大公约数,只要求出6105和2146的最大公约数就可以了。
第二步 对6105和2146重复第一步的做法 6105=2146×2+1813 同理6105和2146的最大公约数也是2146和1813的最大公约数。
完整的过程
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
例2 用辗转相除法求225和135的最大公约数
225=135×1+90
135=90×1+45
90=45×2
显然37是148和37的最大公约数,也就是8251和6105的最大公约数
显然45是90和45的最大公约数,也就是225和135的最大公约数
思考1:从上面的两个例子可以看出计算的规律是什么?
S1:用大数除以小数
S2:除数变成被除数,余数变成除数
S3:重复S1,直到余数为0
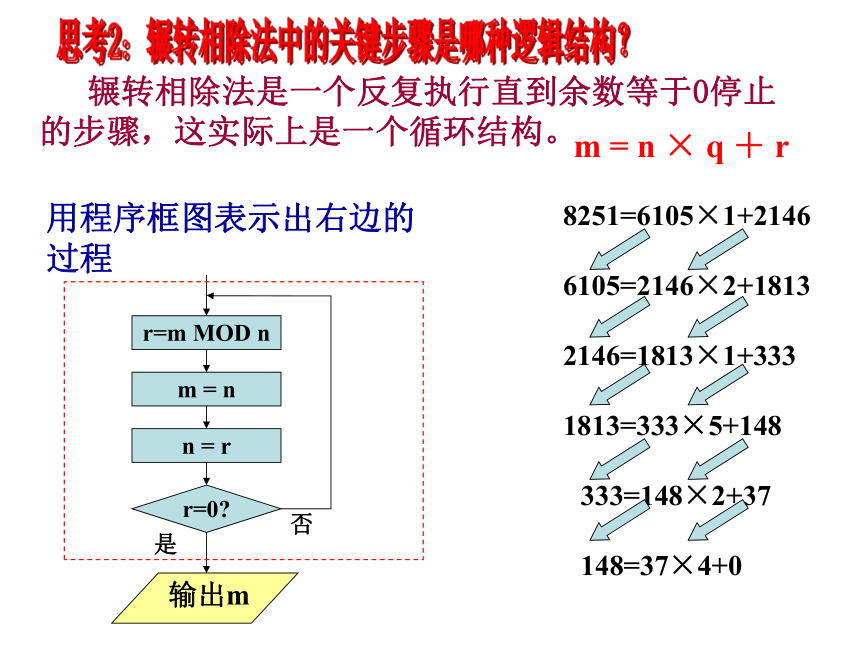
辗转相除法是一个反复执行直到余数等于0停止的步骤,这实际上是一个循环结构。
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
m = n × q + r
用程序框图表示出右边的过程
r=m MOD n
m = n
n = r
r=0
是
否
输出m
1、辗转相除法(欧几里得算法)
(1)算理:
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。
(2)算法步骤
第一步:输入两个正整数m,n(m>n).
第二步:计算m除以n所得的余数r.
第三步:m=n, n=r.
第四步:若r=0,则m,n的最大公约数等于m;
否则转到第二步.
第五步:输出最大公约数m.
(3)程序框图
(4)程序
开始
输入m,n
r=m MOD n
m=n
r=0
是
否
n=r
输出m
结束
INPUT “m,n=“;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
《九章算术》——更相减损术
算理:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。”
第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止,则这个数或这个数与约简数的乘积就是所求的最大公约数。
例3 用更相减损术求98与63的最大公约数
解:由于63不是偶数,把98和63以大数减小数,并辗转相减
98-63=35
63-35 =28
35-28=7
28-7=21
21-7=14
14-7=7
所以,98和63的最大公约数等于7
用更相减损术求两个正数84与72的最大公约数.
练习:
先约简,再求21与18的最大公约数,然后乘以两次约简的质因数4
你能根据“更相减损术”设计程序,求两个正整数的最大公约数吗
思考
例3、求324、243、135这三个数的最大公约数。
思路分析:求三个数的最大公约数可以先求出两个数的最大公约数,第三个数与前两个数的最大公约数的最大公约数即为所求。
比较辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到
小结
算法案例
1. 回顾算法的三种表述:
自然语言
程序框图
程序语言
(三种逻辑结构)
(五种基本语句)
2. 思考:
小学学过的求两个数最大公约数的方法?
先用两个公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来.
1、求两个正整数的最大公约数
(1)求25和35的最大公约数
(2)求18和30的最大公约数
25
(1)
5
5
35
7
18
(2)
2
9
30
15
所以,25和35的最大公约数为5
所以,18和30的最大公约数为6
2、除了用这种方法外还有没有其它方法?
算出8256和6105的最大公约数.
3
3
5
辗转相除法(欧几里得算法)
观察用辗转相除法求8251和6105的最大公约数的过程
第一步 用两数中较大的数除以较小的数,求得商和余数 8251=6105×1+2146
结论: 8251和6105的公约数就是6105和2146的公约数,反之也成立。求8251和6105的最大公约数,只要求出6105和2146的最大公约数就可以了。
第二步 对6105和2146重复第一步的做法 6105=2146×2+1813 同理6105和2146的最大公约数也是2146和1813的最大公约数。
完整的过程
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
例2 用辗转相除法求225和135的最大公约数
225=135×1+90
135=90×1+45
90=45×2
显然37是148和37的最大公约数,也就是8251和6105的最大公约数
显然45是90和45的最大公约数,也就是225和135的最大公约数
思考1:从上面的两个例子可以看出计算的规律是什么?
S1:用大数除以小数
S2:除数变成被除数,余数变成除数
S3:重复S1,直到余数为0
辗转相除法是一个反复执行直到余数等于0停止的步骤,这实际上是一个循环结构。
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
m = n × q + r
用程序框图表示出右边的过程
r=m MOD n
m = n
n = r
r=0
是
否
输出m
1、辗转相除法(欧几里得算法)
(1)算理:
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。
(2)算法步骤
第一步:输入两个正整数m,n(m>n).
第二步:计算m除以n所得的余数r.
第三步:m=n, n=r.
第四步:若r=0,则m,n的最大公约数等于m;
否则转到第二步.
第五步:输出最大公约数m.
(3)程序框图
(4)程序
开始
输入m,n
r=m MOD n
m=n
r=0
是
否
n=r
输出m
结束
INPUT “m,n=“;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
《九章算术》——更相减损术
算理:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。”
第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止,则这个数或这个数与约简数的乘积就是所求的最大公约数。
例3 用更相减损术求98与63的最大公约数
解:由于63不是偶数,把98和63以大数减小数,并辗转相减
98-63=35
63-35 =28
35-28=7
28-7=21
21-7=14
14-7=7
所以,98和63的最大公约数等于7
用更相减损术求两个正数84与72的最大公约数.
练习:
先约简,再求21与18的最大公约数,然后乘以两次约简的质因数4
你能根据“更相减损术”设计程序,求两个正整数的最大公约数吗
思考
例3、求324、243、135这三个数的最大公约数。
思路分析:求三个数的最大公约数可以先求出两个数的最大公约数,第三个数与前两个数的最大公约数的最大公约数即为所求。
比较辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到
小结
