1.3.1有理数的加法第2课时有理数加法的运算律及其应用 课件(共22张PPT)
文档属性
| 名称 | 1.3.1有理数的加法第2课时有理数加法的运算律及其应用 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 08:49:53 | ||
图片预览






文档简介
(共22张PPT)
人教七上数学同步精品课件
人教版七年级上册
第一章 有理数
第2课时 有理数加法的
运算律及其应用
1_3有理数的加减法
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.掌握有理数的加法交换律和结合律.
2.能运用加法交换律、结合律简化运算.
学习目标
重点
难点
小明养了一只小狗,每天早晨给小狗2个罐头,晚上给1个罐头,小狗很不开心,它想不通为什么晚上比早晨少了一个呢?
于是小明改成早晨给小狗1个罐头,晚上给2个罐头. 小狗高兴了,因为它觉得每天晚上都比早晨多吃一个.
罐头的总数
变了吗?
新课引入
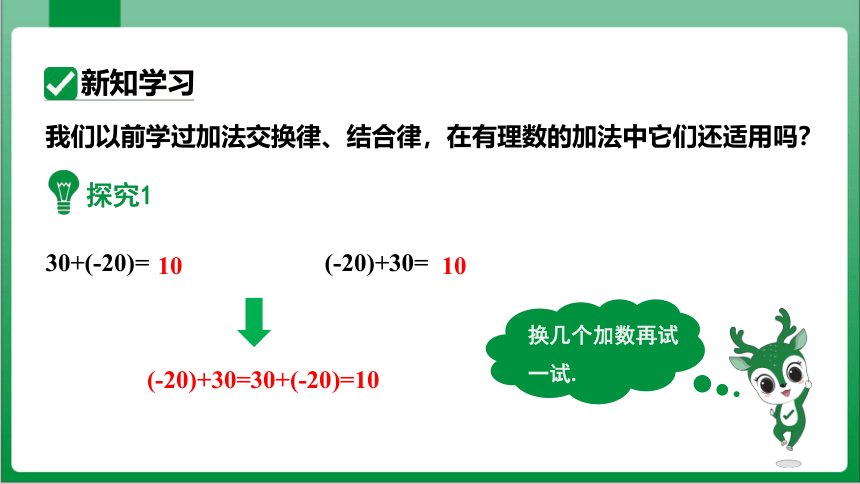
我们以前学过加法交换律、结合律,在有理数的加法中它们还适用吗?
探究1
30+(-20)= (-20)+30=
(-20)+30=30+(-20)=10
换几个加数再试一试.
10
10
新知学习
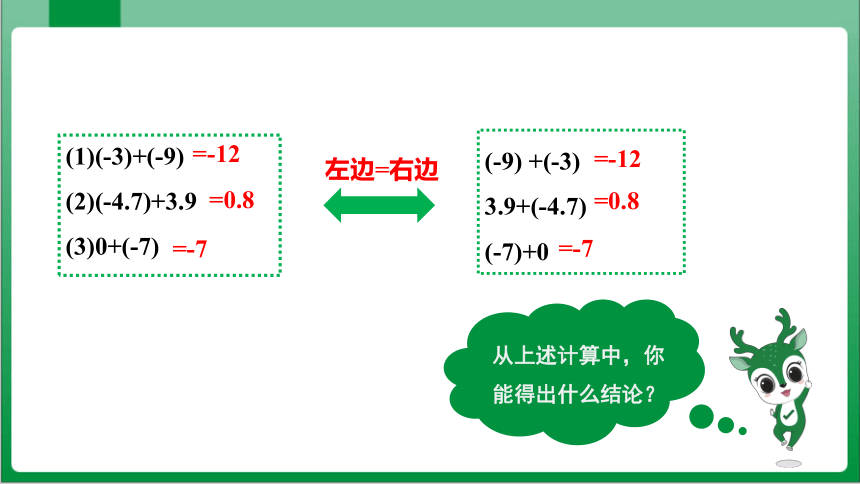
从上述计算中,你能得出什么结论?
(1)(-3)+(-9)
(2)(-4.7)+3.9
(3)0+(-7)
=-12
(-9) +(-3)
3.9+(-4.7)
(-7)+0
=0.8
=-7
=-12
=0.8
=-7
左边=右边
有理数加法的交换律:
两个数相加,交换加数的位置,和不变,
用字母表示为a+b=b+a.
归纳
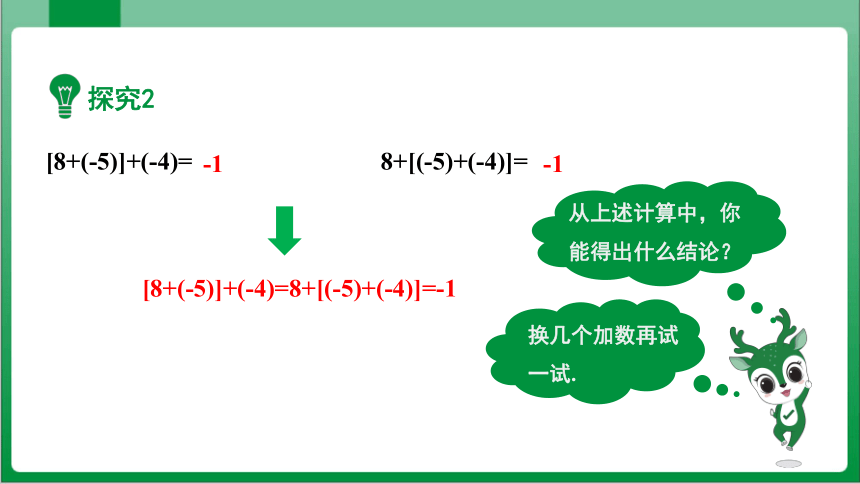
探究2
[8+(-5)]+(-4)= 8+[(-5)+(-4)]=
[8+(-5)]+(-4)=8+[(-5)+(-4)]=-1
换几个加数再试一试.
-1
-1
从上述计算中,你能得出什么结论?
有理数加法的结合律:
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变, 用字母表示为(a+b)+c=a+(b+c).
归纳
例1.计算:(1)16 + (-25) + 24+ (-35).
解: 16 + (-25) + 24+ (-35)
= 16 + 24 + [ (-25) + (-35)]
=40+ (-60)
=-20.
=-18+0+18.7
=0.7
=[(-18.5)+ ]+[(- )+(+ )]+18.7
例2 每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示,10袋小麦的总重量是多少?与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4
再计算总计超过多少千克
905.4-90×10=5.4
答:10袋小麦总重量是905.4千克,总计超过5.4千克.
解法2:每袋小麦超过90千克的千克数记作正数,不足的千克数记作负数.
10袋小麦对应的数分别为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4.
90×10+5.4=905.4.
答:10袋小麦总质量是905.4千克,总计超过5.4千克.
1.计算:
(1)23+(-17)+6+(-22)
=(23+6)+[(-17)+(-22)]
=29-39
=-10
随堂练习
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-3
(2)(-2)+3+1+(-3)+2+(-4)
3.一辆出租车在一条东西方向的路上行驶.如果规定向东为正,向西为负,那么该出租车从出发点开始行驶的路程为:+2,-3,+2,+1,-2,-1,-2 (单位:千米).
(1) 此时,如何描述出租车的位置?
解:(1) (+2)+(-3)+(+2)+(+1)+(-2)+(-1)+(-2)=-3,
所以,此时出租车位于出发点正西方向 3 千米处.
(2) 如果出租车每千米耗油 0.2 升,此时返回出发点,那么此次行程共耗油多少升?
(2) 这辆出租车行驶的总路程为:
|+2|+|-3|+|+2|+|+1|+|-2|+|-1|+|-2|+3=16 (千米).
16×0.2=3.2 (升).
所以,此次行程共耗油 3.2 升.
加法的交换律:
两个数相加,交换加数的位置,和不变
a+b=b+a.
加法运算律
加法结合律:
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变
(a+b)+c=a+(b+c)
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第一章 有理数
第2课时 有理数加法的
运算律及其应用
1_3有理数的加减法
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.掌握有理数的加法交换律和结合律.
2.能运用加法交换律、结合律简化运算.
学习目标
重点
难点
小明养了一只小狗,每天早晨给小狗2个罐头,晚上给1个罐头,小狗很不开心,它想不通为什么晚上比早晨少了一个呢?
于是小明改成早晨给小狗1个罐头,晚上给2个罐头. 小狗高兴了,因为它觉得每天晚上都比早晨多吃一个.
罐头的总数
变了吗?
新课引入
我们以前学过加法交换律、结合律,在有理数的加法中它们还适用吗?
探究1
30+(-20)= (-20)+30=
(-20)+30=30+(-20)=10
换几个加数再试一试.
10
10
新知学习
从上述计算中,你能得出什么结论?
(1)(-3)+(-9)
(2)(-4.7)+3.9
(3)0+(-7)
=-12
(-9) +(-3)
3.9+(-4.7)
(-7)+0
=0.8
=-7
=-12
=0.8
=-7
左边=右边
有理数加法的交换律:
两个数相加,交换加数的位置,和不变,
用字母表示为a+b=b+a.
归纳
探究2
[8+(-5)]+(-4)= 8+[(-5)+(-4)]=
[8+(-5)]+(-4)=8+[(-5)+(-4)]=-1
换几个加数再试一试.
-1
-1
从上述计算中,你能得出什么结论?
有理数加法的结合律:
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变, 用字母表示为(a+b)+c=a+(b+c).
归纳
例1.计算:(1)16 + (-25) + 24+ (-35).
解: 16 + (-25) + 24+ (-35)
= 16 + 24 + [ (-25) + (-35)]
=40+ (-60)
=-20.
=-18+0+18.7
=0.7
=[(-18.5)+ ]+[(- )+(+ )]+18.7
例2 每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示,10袋小麦的总重量是多少?与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4
再计算总计超过多少千克
905.4-90×10=5.4
答:10袋小麦总重量是905.4千克,总计超过5.4千克.
解法2:每袋小麦超过90千克的千克数记作正数,不足的千克数记作负数.
10袋小麦对应的数分别为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4.
90×10+5.4=905.4.
答:10袋小麦总质量是905.4千克,总计超过5.4千克.
1.计算:
(1)23+(-17)+6+(-22)
=(23+6)+[(-17)+(-22)]
=29-39
=-10
随堂练习
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-3
(2)(-2)+3+1+(-3)+2+(-4)
3.一辆出租车在一条东西方向的路上行驶.如果规定向东为正,向西为负,那么该出租车从出发点开始行驶的路程为:+2,-3,+2,+1,-2,-1,-2 (单位:千米).
(1) 此时,如何描述出租车的位置?
解:(1) (+2)+(-3)+(+2)+(+1)+(-2)+(-1)+(-2)=-3,
所以,此时出租车位于出发点正西方向 3 千米处.
(2) 如果出租车每千米耗油 0.2 升,此时返回出发点,那么此次行程共耗油多少升?
(2) 这辆出租车行驶的总路程为:
|+2|+|-3|+|+2|+|+1|+|-2|+|-1|+|-2|+3=16 (千米).
16×0.2=3.2 (升).
所以,此次行程共耗油 3.2 升.
加法的交换律:
两个数相加,交换加数的位置,和不变
a+b=b+a.
加法运算律
加法结合律:
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变
(a+b)+c=a+(b+c)
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
