1.2.1 有理数 课件(共18张PPT)【2023秋人教七上数学高效实用备课】
文档属性
| 名称 | 1.2.1 有理数 课件(共18张PPT)【2023秋人教七上数学高效实用备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 20:44:27 | ||
图片预览





文档简介
(共18张PPT)
人教七上数学同步精品课件
人教版七年级上册
第一章 有理数
1.2.1 有理数
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.掌握有理数的概念.
2.会对有理数按一定的标准进行分类.
学习目标
重点
重点
-1, ,1,-0.5,2,-3,0, ,0.1,0.3, ,2.25
在下面这些数中,正整数有哪些?负整数有哪些?正分数有哪些?
负分数有哪些?
正整数:1,2,
负整数:-1,-3,
正分数: ,0.1,0.3,2.25
负分数:-0.5, ,
新课引入
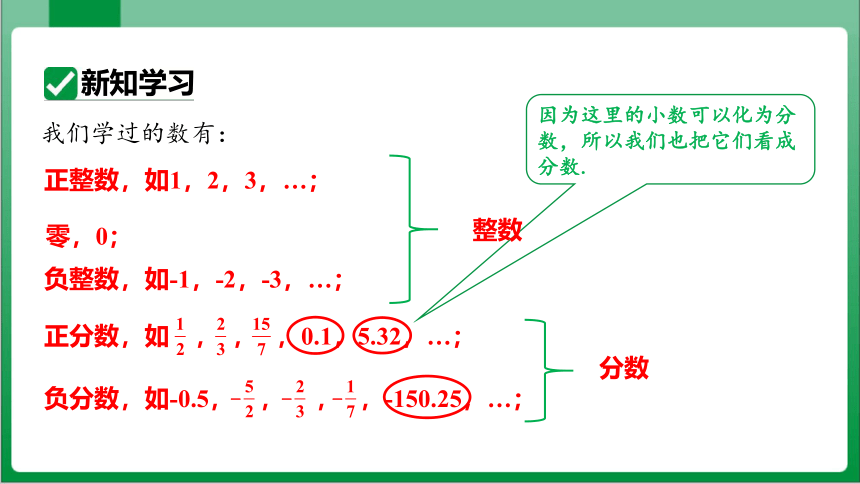
因为这里的小数可以化为分数,所以我们也把它们看成分数.
我们学过的数有:
正整数,如1,2,3,…;
零,0;
负整数,如-1,-2,-3,…;
负分数,如-0.5, , , ,-150.25,…;
正分数,如 , , ,0.1,5.32,…;
整数
分数
新知学习
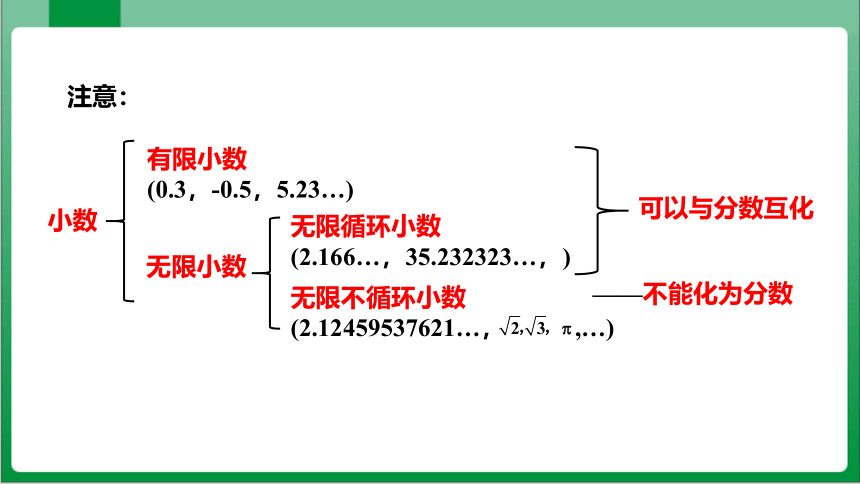
注意:
可以与分数互化
——不能化为分数
小数
有限小数
(0.3,-0.5,5.23…)
无限小数
无限循环小数
(2.166…,35.232323…,)
无限不循环小数
(2.12459537621…, ,…)
正整数
0
负整数
正分数
负分数
整数
分数
整数和分数统称有理数.
有理数
归纳
从小学开始,我们首先认识了正整数,后来又增加了0和正分数,在认识了负整数和负分数后,对数的认识就扩充到了有理数范围.
按定义分类:
有理数按符号(正、负)分类如下:
注意:零是整数,但零既不是正数,也不是负数.
例1 判断表中各数分别属于哪类数,在相应的空格内打“√”.
正数 负数 整数 分数 有理数
-15
6
-4.9
0
-12
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
例2 所有正数组成正数集合,所有负数组成负数集合,所有整数组成整数集合,将下列各数填入下图所示的相应的圈内.
-1,0,2,
正数集合
整数集合
负数集合
分析:圈中的公共部分的意义:各个集合的公共部分;题中2既是正数,也是整数;-3,-1既是整数,又是负数.
1.指出下列各数中的正数、负数、整数、分数:
-15,+6,-2,-0.9, 1, ,0, ,0.63,-4. 95.
正数:+6,1, , ,0.63
负数:-15,-2,-0.9,-4. 95
整数: -15,+6,-2,1,0,
分数:-0.9, , ,0.63,-4. 95
随堂练习
2.下列说法中,正确的是( )
A.正整数、负整数统称为整数;
B.正分数、负分数统称为分数;
C.零既可以是正整数,也可以是负整数;
D.一个有理数不是正数就是负数.
B
3.在下列各数中:
,非负整数的个数是 .
2
非负整数包括0和正整数哦.
4.(中考·丽水)在数 0,2,-3,-1.2 中,属于负整数的是 ( )
A.0 B.2 C.-3 D.-1.2
C
5. (2020广西)下列实数不是有理数的是( )
A. π B. 1 C. 0 D. -5
A
有理数按定义分类:
有理数按符号(正、负)分类:
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第一章 有理数
1.2.1 有理数
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.掌握有理数的概念.
2.会对有理数按一定的标准进行分类.
学习目标
重点
重点
-1, ,1,-0.5,2,-3,0, ,0.1,0.3, ,2.25
在下面这些数中,正整数有哪些?负整数有哪些?正分数有哪些?
负分数有哪些?
正整数:1,2,
负整数:-1,-3,
正分数: ,0.1,0.3,2.25
负分数:-0.5, ,
新课引入
因为这里的小数可以化为分数,所以我们也把它们看成分数.
我们学过的数有:
正整数,如1,2,3,…;
零,0;
负整数,如-1,-2,-3,…;
负分数,如-0.5, , , ,-150.25,…;
正分数,如 , , ,0.1,5.32,…;
整数
分数
新知学习
注意:
可以与分数互化
——不能化为分数
小数
有限小数
(0.3,-0.5,5.23…)
无限小数
无限循环小数
(2.166…,35.232323…,)
无限不循环小数
(2.12459537621…, ,…)
正整数
0
负整数
正分数
负分数
整数
分数
整数和分数统称有理数.
有理数
归纳
从小学开始,我们首先认识了正整数,后来又增加了0和正分数,在认识了负整数和负分数后,对数的认识就扩充到了有理数范围.
按定义分类:
有理数按符号(正、负)分类如下:
注意:零是整数,但零既不是正数,也不是负数.
例1 判断表中各数分别属于哪类数,在相应的空格内打“√”.
正数 负数 整数 分数 有理数
-15
6
-4.9
0
-12
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
例2 所有正数组成正数集合,所有负数组成负数集合,所有整数组成整数集合,将下列各数填入下图所示的相应的圈内.
-1,0,2,
正数集合
整数集合
负数集合
分析:圈中的公共部分的意义:各个集合的公共部分;题中2既是正数,也是整数;-3,-1既是整数,又是负数.
1.指出下列各数中的正数、负数、整数、分数:
-15,+6,-2,-0.9, 1, ,0, ,0.63,-4. 95.
正数:+6,1, , ,0.63
负数:-15,-2,-0.9,-4. 95
整数: -15,+6,-2,1,0,
分数:-0.9, , ,0.63,-4. 95
随堂练习
2.下列说法中,正确的是( )
A.正整数、负整数统称为整数;
B.正分数、负分数统称为分数;
C.零既可以是正整数,也可以是负整数;
D.一个有理数不是正数就是负数.
B
3.在下列各数中:
,非负整数的个数是 .
2
非负整数包括0和正整数哦.
4.(中考·丽水)在数 0,2,-3,-1.2 中,属于负整数的是 ( )
A.0 B.2 C.-3 D.-1.2
C
5. (2020广西)下列实数不是有理数的是( )
A. π B. 1 C. 0 D. -5
A
有理数按定义分类:
有理数按符号(正、负)分类:
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
