2023-2024学年人教版数学八年级上册13.1 轴对称一一线段的垂值平分线的性质(1) 提能训训练 (无答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册13.1 轴对称一一线段的垂值平分线的性质(1) 提能训训练 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 244.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 00:00:00 | ||
图片预览


文档简介
第1课 轴对称——线段的垂直平分线的性质(1)
提能训练
★重点练习 线段的垂直平分线的性质
(1)线段垂直平分线上的点与这条线段两个端点的距离;
(2)几何语言:
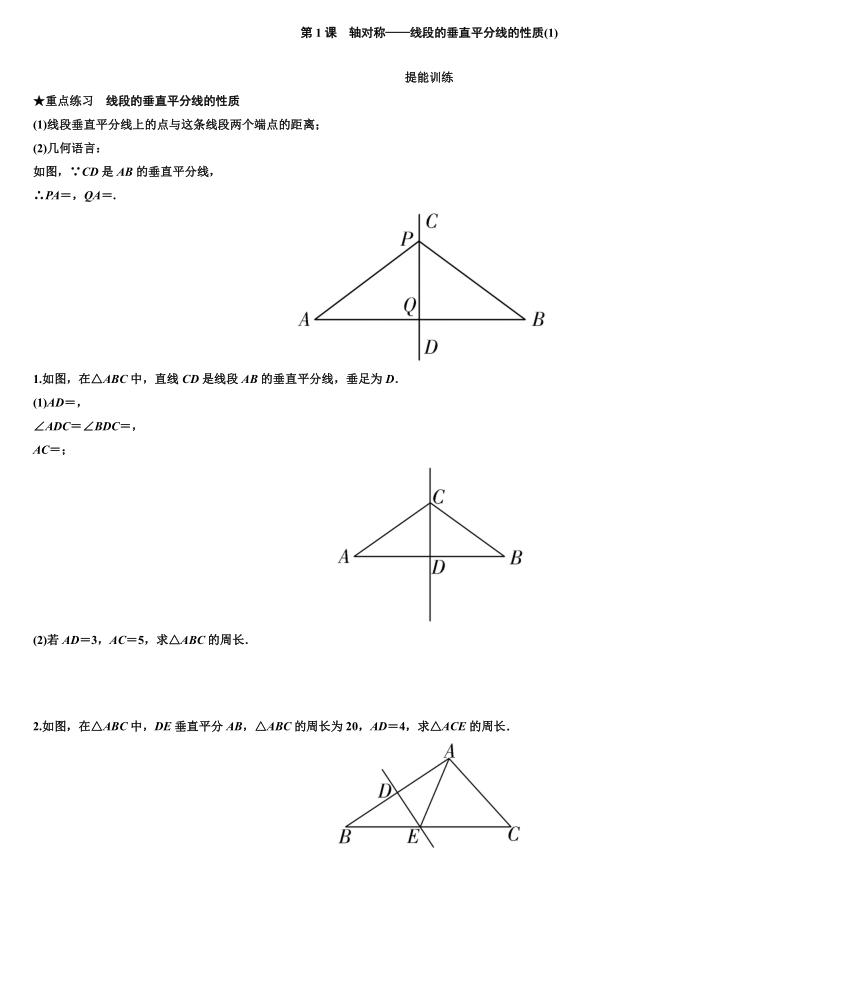
如图,∵CD是AB的垂直平分线,
∴PA=,QA=.
1.如图,在△ABC中,直线CD是线段AB的垂直平分线,垂足为D.
(1)AD=,
∠ADC=∠BDC=,
AC=;
(2)若AD=3,AC=5,求△ABC的周长.
2.如图,在△ABC中,DE垂直平分AB,△ABC的周长为20,AD=4,求△ACE的周长.
(1)与线段两个端点距离相等的点在这条线段的上;
(2)几何语言:
如图,∵,直线m是线段AB的垂直平分线,
∴点P在直线m上.
3.如图,点E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别为C,D.
求证:(1)△OCE≌△ODE;
(2)OE是线段CD的垂直平分线.
4.如图,∠C=∠D=90°,AC与BD交于点O,AC=BD.
求证:(1)AD=BC;
(2)点O在线段AB的垂直平分线上.
强化训练
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.在锐角△ABC内有一点P,满足PA=PB=PC,则点P是△ABC的( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
3.如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为( )
A.25
B.22
C.19
D.18
4.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于点D,E,若∠CAE=∠B+18°,则∠B的度数为.
5.如图,在△ABC中,DM,EN分别垂直平分AC和BC,分别交AB于M,N两点,DM与EN相交于点F.
(1)若△CMN的周长为15 cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
6.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE并延长,交BC的延长线于点F,连接BE,且BE⊥AF.求证:点B在线段AF的垂直平分线上.
提能训练
★重点练习 线段的垂直平分线的性质
(1)线段垂直平分线上的点与这条线段两个端点的距离;
(2)几何语言:
如图,∵CD是AB的垂直平分线,
∴PA=,QA=.
1.如图,在△ABC中,直线CD是线段AB的垂直平分线,垂足为D.
(1)AD=,
∠ADC=∠BDC=,
AC=;
(2)若AD=3,AC=5,求△ABC的周长.
2.如图,在△ABC中,DE垂直平分AB,△ABC的周长为20,AD=4,求△ACE的周长.
(1)与线段两个端点距离相等的点在这条线段的上;
(2)几何语言:
如图,∵,直线m是线段AB的垂直平分线,
∴点P在直线m上.
3.如图,点E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别为C,D.
求证:(1)△OCE≌△ODE;
(2)OE是线段CD的垂直平分线.
4.如图,∠C=∠D=90°,AC与BD交于点O,AC=BD.
求证:(1)AD=BC;
(2)点O在线段AB的垂直平分线上.
强化训练
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.在锐角△ABC内有一点P,满足PA=PB=PC,则点P是△ABC的( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
3.如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为( )
A.25
B.22
C.19
D.18
4.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于点D,E,若∠CAE=∠B+18°,则∠B的度数为.
5.如图,在△ABC中,DM,EN分别垂直平分AC和BC,分别交AB于M,N两点,DM与EN相交于点F.
(1)若△CMN的周长为15 cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
6.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE并延长,交BC的延长线于点F,连接BE,且BE⊥AF.求证:点B在线段AF的垂直平分线上.
