3.2勾股定理的逆定理 课件(共30张PPT)
文档属性
| 名称 | 3.2勾股定理的逆定理 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 15:23:54 | ||
图片预览









文档简介
第3章 · 勾股定理
3.2 勾股定理的逆定理
学习目标
1. 探究并证明勾股定理逆定理,体会“数”与“形”的内在联系;
2. 会应用勾股定理的逆定理判定一个三角形是否是直角三角形;
3. 知道“勾股数”的意义.
问题情境
上节课我们学习了:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
反过来,
如果一个三角形的两边平方和等于第三边的平方,那么这个三角形是直角三角形吗?
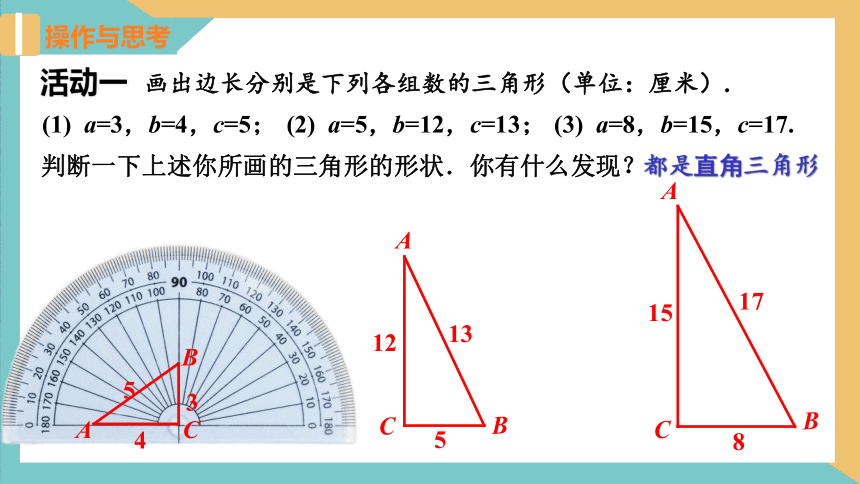
活动一 画出边长分别是下列各组数的三角形(单位:厘米).
操作与思考
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
B
3
4
C
A
5
B
5
12
C
A
13
B
8
15
C
A
17
判断一下上述你所画的三角形的形状.你有什么发现?
都是直角三角形
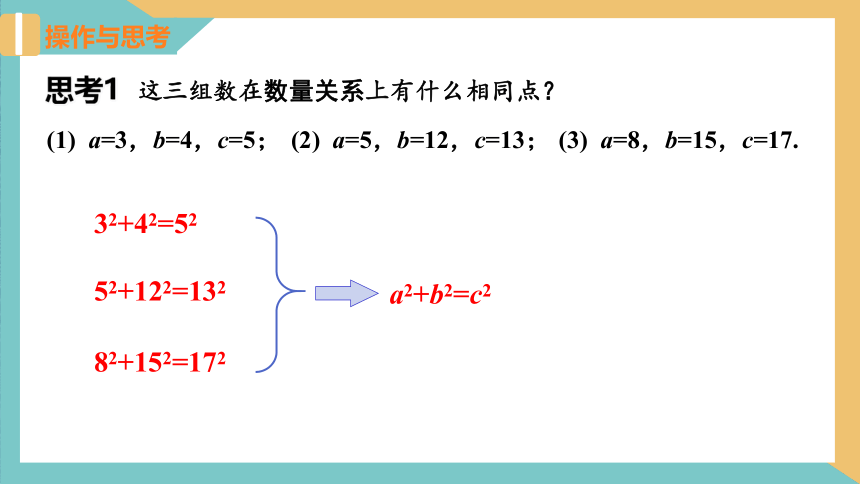
思考1 这三组数在数量关系上有什么相同点?
操作与思考
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
82+152=172
32+42=52
52+122=132
a2+b2=c2
思考2 根据上述结论你有什么猜想呢?
操作与思考
猜想:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
你能证明这个猜想吗?
A
b
a
C
B
c
已知:在△ABC中,AB=c , BC=a, CA=b, 且a2+b2=c2.
求证:△ ABC是直角三角形.
操作与思考
A
b
a
C
B
c
A′
b
a
C′
B′
∟
证明:画一个△A′B′C′,使∠C′=90°,B′C′=a, A′C′=b(如图).
由勾股定理,可得 A′B′ 2= a2+b2.
因为 AB2= a2+b2,
根据“SSS”,可证△ABC ≌△A′ B′ C′ .
于是,∠C=∠C′=90°,△ABC是直角三角形.
新知归纳
勾股定理的逆定理:
如果三角形的三边长a、b、c,且a2 + b2 = c2,那么这个三角形是直角三角形.
A
b
a
C
B
c
符号语言:
在△ABC中,
∵a?+b?=c?,
∴△ABC为直角三角形.
作用:判定一个三角形是否是直角三角形.
这个结论与勾股定理有什么关系呢?
哪个角是直角
最长边所对应的角为直角,∠C=90°.
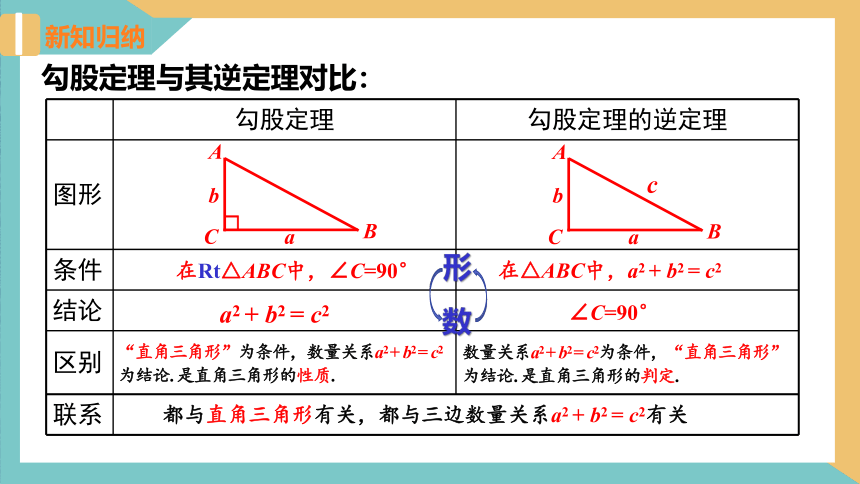
新知归纳
勾股定理与其逆定理对比:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
勾股定理
勾股定理的逆定理
图形
条件
结论
区别
联系
A
b
a
C
B
∟
在Rt△ABC中,∠C=90°
a2 + b2 = c2
“直角三角形”为条件,数量关系a2 + b2 = c2为结论. 是直角三角形的性质.
A
b
a
C
B
c
都与直角三角形有关,都与三边数量关系a2 + b2 = c2有关
在△ABC中,a2 + b2 = c2
∠C=90°
数量关系a2 + b2 = c2为条件,“直角三角形”为结论. 是直角三角形的判定.
形
数
新知应用
(1) a=8,b=15,c=17;
(2) a=13,b=14,c=15.
下面以a、b、c为边长的三角形是不是直角三角形?若是,请指出哪个角是直角.
解:(1) ∵82+152=64+225=289,172=289,
∴ 82+152=172.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
(2) ∵132+142=365,152=225,
∴ 132+142≠152,不符合勾股定理的逆定理,
∴ 这个三角形不是直角三角形.
新知巩固
(1) a=7,b=25,c=24;
判断由a、b、c组成的三角形是不是直角三角形,若是,请指出哪个角是直角.
(2) a:b:c=3:4:5.
解:(1) ∵72+242=49+576=625,252=625,
∴ 72+242=252.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠B是直角.
(2)设a=3k、b=4k、c=5k,
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
新知归纳
运用勾股定理的逆定理判断直角三角形的一般步骤:
1.找:确定三角形的最长边;
2.算:分别计算出最长边的平方与另两边的平方和;
3.比:通过比较来判断最长边的平方与另两边的平方和是否相等;
4.判:作出结论,若相等,则说明这个三角形是直角三角形,否则不
是直角三角形.
例题讲解
例1 像(3,4,5)、(6,8,10)、(5,12,13)等满足a2+b2=c2的三个正整数,通常称为勾股数,请你填表并探索规律.
{5940675A-B579-460E-94D1-54222C63F5DA}a
3
6
9
12
…
3n
b
4
8
12
16
…
4n
c
5
10
15
20
…
5n
{5940675A-B579-460E-94D1-54222C63F5DA}a
3
5
7
9
11
…
2n+1
b
4
12
24
40
60
…
2n(n+1)
c
5
13
25
41
61
…
2n(n+1)+1
①从上面2个表中你能发现什么规律?
②你能根据发现的规律写出更多的勾股数吗?试试看 .
解:①规律:一组勾股数,都扩大相同倍数n(n为正整数),得到一组新数,这组数同样是勾股数.
勾股数的性质
例题讲解
②答案不唯一,如:15,20,25;13,84,85等.
利用勾股数可以构造直角三角形.
知识窗
美国哥伦比亚大学图书馆收藏着一块编号为“普林顿322”(plimpton322)的古巴比伦泥板. 泥板上的一些神秘符号揭示了什么奥秘呢?
翻译图
经过专家的潜心研究,发现其中两列数字竟然是直角三角形的勾和弦的长,只要再添加一列数(如图左边的一列),那么每行的三个数就是一个直角三角形三边的边长.这些数组都是勾股数组. 人们经过研究发现:勾股数有无数多组.
新知巩固
例2 如图是由边长为1的小正方形组成的网格.
(1) 你能判断AD与CD的位置关系吗?说出你的理由.
(2) 求四边形ABCD的面积.
{5940675A-B579-460E-94D1-54222C63F5DA}
A
B
C
D
解:(1)
∵ AD2=1+4=5,CD2=4+16=20 ,AC= 5
连接AC.
∴ AD2+CD2=25,AC2=25
∴ AD2+CD2=AC2
∴ 由勾股定理的逆定理得:∠CAD=90°.
∴ AD⊥CD
(2) S四边形ABCD=S△ADC+S△ABC
=????????×5×2+????????×5×3=????????????
?
1. 下列是直角三角形的有(?? ? )个
①△ABC中a?=c?-b?;
②△ABC的三内角之比为3:4:7;
③ △ABC的三边平方之比为1:2:3;
④ 三角形三边之比为3:4:5
A.1 B.2 C.3 D.4
D
新知巩固
归纳总结
用角判断:
1.两个锐角互余 的三角形是直角三角形;
2.有一个角是90°的三角形是直角三角形;
用边判断:
如果已知条件与边有关,则可通过勾股定理的逆定理(a?+b?=c?)进行判断.
判断三角形是直角三角形的方法:
新知巩固
2.下列各组数中,是勾股数的为( )
A. ????????、????????、???????? B. 0.6、0.8、1.0
C. 1、2、3 D. 3k、4k、5k(k为正整数)
?
D
判断三个数是不是勾股数的“三步法”:
(1)判断三个数是否都为正整数;
(2)确定最大数;
(3)计算较小两数的平方和是否等于最大数的平方.
3. △ABC的三边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1.
问:△ABC是直角三角形吗?证明你的结论.
解:∵AB?+BC?=(n?-1)?+(2n)?
=n4 -2n?+1+4n?
=n4 +2n?+1
=(n?+1)?
=AC?,
∴ 由勾股定理的逆定理得△ABC直角三角形,边AC所对的角是直角.
新知巩固
4.如图,AD⊥BC,垂足为D. 如果CD=1,AD=2,BD=4,那么∠BAC是直角吗?请说明理由.
C
A
B
D
∟
新知巩固
解:∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∴ 在Rt△ADC中,AC2=AD2+DC2=22+12=5.
在Rt△ADB中,AB2=AD2+BD2=22+42=20.
∵AC2+AB2=20+5=25,BC2=52=25.
∴AC2+AB2=BC2.
∴△ABC直角三角形,∠BAC=90°.
1
2
4
课堂小结
勾股定理的逆定理
内容
应用
勾股数
a2+b2=c2
直角三角形且∠C=90°
判定一个三角形为直角三角形
满足a2+b2=c2的三个正整数
注意:最长边不一定是c, ∠C也不一定是直角.
当堂检测
1.下列各数组中,不能作为直角三角形的三边长的是( ) A.3,4,5 B.10,6,8
C.4,5,6 D.12,13,5
C
2.下列各组数是勾股数的是 ( )
A. 6,8,10 B. 7,8,9
C. 0.3,0.4,0.5 D. 52,122,132
A
当堂检测
3. 在△ABC中,∠A,∠B,∠C的对边分别是 a,b,c,那么下面不能判定△ABC是直角三角形的是( )
A. ∠A=∠C=∠B
B. ????????=(????+????)(?????????)
C. ∠A:∠B:∠C=5 :4 :3
D. a : b : c=5 : 4 : 3
?
C
当堂检测
4.如图所示正方形网格中的△ABC,若小方的格边长为1,则△ABC的形状为 ( )
A. 直角三角形
B. 锐角三角形
C. 钝角三角形
D. 以上答案都不对
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
C
B
当堂检测
5. △ABC的三边分别是a、b、c且满足|a-8 |+(b-6)2=0,则当c2=_______时,△ABC是直角三角形.
100或28
4.若一个三角形的三边长满足a2-b2=c2,则这个三角形一定是 ________三角形.
直角
当堂检测
解:
∴ 根据勾股定理的逆定理得该三角形是直角三角形.
172=289,
∵152+82=289,
∴ S=????????×????????×????=60cm2.
?
6.若一个三角形的三边长分别为8 cm,15 cm,17 cm,求该三角形的面积及最长边上的高.
令斜边上的高为x cm,则有17x=8×15,
∴ x=????????????????????cm,∴最长边上的高为????????????????????cm.
?
7. 在△ABC中,D为BC边上的点.已知AB=13,AD=12,AC=15,BD=5,求DC的长.
A
B
C
D
解:∵AB=13,AD=12,BD=5,
∴ AB2=AD2+BD2.
∴ 由勾股定理的逆定理得:△ABD是直角三角形,且∠ADB=90°.
∴∠ADC=90°.在Rt△ADC中,AC2=AD2+DC2.
∵AD=12,AC=15,
∴DC2=AC2-AD2=152-122=92.
∴ DC=9.
当堂检测
当堂检测
8.观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.根据你发现的规律,请写出:(1)当a=19时,b=________,c=________;
(2)当a=2n+1时,求b,c的值;
180
181
解:通过观察知c-b=1,
∵(2n+1)2+b2=c2,∴c2-b2=(2n+1)2,(b+c)(c-b)=(2n+1)2,∴b+c=(2n+1)2.又∵c=b+1,
∴2b+1=(2n+1)2,∴b=2n2+2n,c=2n2+2n+1.
当堂检测
(3)用(2)的结论判断15,111,112是否为一组勾股数,并说明理由.
解:不是.理由如下:由(2)知,2n+1,2n2+2n,2n2+2n+1为一组勾股数,当n=7时,2n+1=15,112-111=1,但2n2+2n=112≠111,∴15,111,112不是一组勾股数.
3.2 勾股定理的逆定理
学习目标
1. 探究并证明勾股定理逆定理,体会“数”与“形”的内在联系;
2. 会应用勾股定理的逆定理判定一个三角形是否是直角三角形;
3. 知道“勾股数”的意义.
问题情境
上节课我们学习了:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
反过来,
如果一个三角形的两边平方和等于第三边的平方,那么这个三角形是直角三角形吗?
活动一 画出边长分别是下列各组数的三角形(单位:厘米).
操作与思考
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
B
3
4
C
A
5
B
5
12
C
A
13
B
8
15
C
A
17
判断一下上述你所画的三角形的形状.你有什么发现?
都是直角三角形
思考1 这三组数在数量关系上有什么相同点?
操作与思考
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
82+152=172
32+42=52
52+122=132
a2+b2=c2
思考2 根据上述结论你有什么猜想呢?
操作与思考
猜想:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
你能证明这个猜想吗?
A
b
a
C
B
c
已知:在△ABC中,AB=c , BC=a, CA=b, 且a2+b2=c2.
求证:△ ABC是直角三角形.
操作与思考
A
b
a
C
B
c
A′
b
a
C′
B′
∟
证明:画一个△A′B′C′,使∠C′=90°,B′C′=a, A′C′=b(如图).
由勾股定理,可得 A′B′ 2= a2+b2.
因为 AB2= a2+b2,
根据“SSS”,可证△ABC ≌△A′ B′ C′ .
于是,∠C=∠C′=90°,△ABC是直角三角形.
新知归纳
勾股定理的逆定理:
如果三角形的三边长a、b、c,且a2 + b2 = c2,那么这个三角形是直角三角形.
A
b
a
C
B
c
符号语言:
在△ABC中,
∵a?+b?=c?,
∴△ABC为直角三角形.
作用:判定一个三角形是否是直角三角形.
这个结论与勾股定理有什么关系呢?
哪个角是直角
最长边所对应的角为直角,∠C=90°.
新知归纳
勾股定理与其逆定理对比:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
勾股定理
勾股定理的逆定理
图形
条件
结论
区别
联系
A
b
a
C
B
∟
在Rt△ABC中,∠C=90°
a2 + b2 = c2
“直角三角形”为条件,数量关系a2 + b2 = c2为结论. 是直角三角形的性质.
A
b
a
C
B
c
都与直角三角形有关,都与三边数量关系a2 + b2 = c2有关
在△ABC中,a2 + b2 = c2
∠C=90°
数量关系a2 + b2 = c2为条件,“直角三角形”为结论. 是直角三角形的判定.
形
数
新知应用
(1) a=8,b=15,c=17;
(2) a=13,b=14,c=15.
下面以a、b、c为边长的三角形是不是直角三角形?若是,请指出哪个角是直角.
解:(1) ∵82+152=64+225=289,172=289,
∴ 82+152=172.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
(2) ∵132+142=365,152=225,
∴ 132+142≠152,不符合勾股定理的逆定理,
∴ 这个三角形不是直角三角形.
新知巩固
(1) a=7,b=25,c=24;
判断由a、b、c组成的三角形是不是直角三角形,若是,请指出哪个角是直角.
(2) a:b:c=3:4:5.
解:(1) ∵72+242=49+576=625,252=625,
∴ 72+242=252.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠B是直角.
(2)设a=3k、b=4k、c=5k,
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
新知归纳
运用勾股定理的逆定理判断直角三角形的一般步骤:
1.找:确定三角形的最长边;
2.算:分别计算出最长边的平方与另两边的平方和;
3.比:通过比较来判断最长边的平方与另两边的平方和是否相等;
4.判:作出结论,若相等,则说明这个三角形是直角三角形,否则不
是直角三角形.
例题讲解
例1 像(3,4,5)、(6,8,10)、(5,12,13)等满足a2+b2=c2的三个正整数,通常称为勾股数,请你填表并探索规律.
{5940675A-B579-460E-94D1-54222C63F5DA}a
3
6
9
12
…
3n
b
4
8
12
16
…
4n
c
5
10
15
20
…
5n
{5940675A-B579-460E-94D1-54222C63F5DA}a
3
5
7
9
11
…
2n+1
b
4
12
24
40
60
…
2n(n+1)
c
5
13
25
41
61
…
2n(n+1)+1
①从上面2个表中你能发现什么规律?
②你能根据发现的规律写出更多的勾股数吗?试试看 .
解:①规律:一组勾股数,都扩大相同倍数n(n为正整数),得到一组新数,这组数同样是勾股数.
勾股数的性质
例题讲解
②答案不唯一,如:15,20,25;13,84,85等.
利用勾股数可以构造直角三角形.
知识窗
美国哥伦比亚大学图书馆收藏着一块编号为“普林顿322”(plimpton322)的古巴比伦泥板. 泥板上的一些神秘符号揭示了什么奥秘呢?
翻译图
经过专家的潜心研究,发现其中两列数字竟然是直角三角形的勾和弦的长,只要再添加一列数(如图左边的一列),那么每行的三个数就是一个直角三角形三边的边长.这些数组都是勾股数组. 人们经过研究发现:勾股数有无数多组.
新知巩固
例2 如图是由边长为1的小正方形组成的网格.
(1) 你能判断AD与CD的位置关系吗?说出你的理由.
(2) 求四边形ABCD的面积.
{5940675A-B579-460E-94D1-54222C63F5DA}
A
B
C
D
解:(1)
∵ AD2=1+4=5,CD2=4+16=20 ,AC= 5
连接AC.
∴ AD2+CD2=25,AC2=25
∴ AD2+CD2=AC2
∴ 由勾股定理的逆定理得:∠CAD=90°.
∴ AD⊥CD
(2) S四边形ABCD=S△ADC+S△ABC
=????????×5×2+????????×5×3=????????????
?
1. 下列是直角三角形的有(?? ? )个
①△ABC中a?=c?-b?;
②△ABC的三内角之比为3:4:7;
③ △ABC的三边平方之比为1:2:3;
④ 三角形三边之比为3:4:5
A.1 B.2 C.3 D.4
D
新知巩固
归纳总结
用角判断:
1.两个锐角互余 的三角形是直角三角形;
2.有一个角是90°的三角形是直角三角形;
用边判断:
如果已知条件与边有关,则可通过勾股定理的逆定理(a?+b?=c?)进行判断.
判断三角形是直角三角形的方法:
新知巩固
2.下列各组数中,是勾股数的为( )
A. ????????、????????、???????? B. 0.6、0.8、1.0
C. 1、2、3 D. 3k、4k、5k(k为正整数)
?
D
判断三个数是不是勾股数的“三步法”:
(1)判断三个数是否都为正整数;
(2)确定最大数;
(3)计算较小两数的平方和是否等于最大数的平方.
3. △ABC的三边长分别是a、b、c,且a=n2-1,b=2n,c=n2+1.
问:△ABC是直角三角形吗?证明你的结论.
解:∵AB?+BC?=(n?-1)?+(2n)?
=n4 -2n?+1+4n?
=n4 +2n?+1
=(n?+1)?
=AC?,
∴ 由勾股定理的逆定理得△ABC直角三角形,边AC所对的角是直角.
新知巩固
4.如图,AD⊥BC,垂足为D. 如果CD=1,AD=2,BD=4,那么∠BAC是直角吗?请说明理由.
C
A
B
D
∟
新知巩固
解:∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∴ 在Rt△ADC中,AC2=AD2+DC2=22+12=5.
在Rt△ADB中,AB2=AD2+BD2=22+42=20.
∵AC2+AB2=20+5=25,BC2=52=25.
∴AC2+AB2=BC2.
∴△ABC直角三角形,∠BAC=90°.
1
2
4
课堂小结
勾股定理的逆定理
内容
应用
勾股数
a2+b2=c2
直角三角形且∠C=90°
判定一个三角形为直角三角形
满足a2+b2=c2的三个正整数
注意:最长边不一定是c, ∠C也不一定是直角.
当堂检测
1.下列各数组中,不能作为直角三角形的三边长的是( ) A.3,4,5 B.10,6,8
C.4,5,6 D.12,13,5
C
2.下列各组数是勾股数的是 ( )
A. 6,8,10 B. 7,8,9
C. 0.3,0.4,0.5 D. 52,122,132
A
当堂检测
3. 在△ABC中,∠A,∠B,∠C的对边分别是 a,b,c,那么下面不能判定△ABC是直角三角形的是( )
A. ∠A=∠C=∠B
B. ????????=(????+????)(?????????)
C. ∠A:∠B:∠C=5 :4 :3
D. a : b : c=5 : 4 : 3
?
C
当堂检测
4.如图所示正方形网格中的△ABC,若小方的格边长为1,则△ABC的形状为 ( )
A. 直角三角形
B. 锐角三角形
C. 钝角三角形
D. 以上答案都不对
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
C
B
当堂检测
5. △ABC的三边分别是a、b、c且满足|a-8 |+(b-6)2=0,则当c2=_______时,△ABC是直角三角形.
100或28
4.若一个三角形的三边长满足a2-b2=c2,则这个三角形一定是 ________三角形.
直角
当堂检测
解:
∴ 根据勾股定理的逆定理得该三角形是直角三角形.
172=289,
∵152+82=289,
∴ S=????????×????????×????=60cm2.
?
6.若一个三角形的三边长分别为8 cm,15 cm,17 cm,求该三角形的面积及最长边上的高.
令斜边上的高为x cm,则有17x=8×15,
∴ x=????????????????????cm,∴最长边上的高为????????????????????cm.
?
7. 在△ABC中,D为BC边上的点.已知AB=13,AD=12,AC=15,BD=5,求DC的长.
A
B
C
D
解:∵AB=13,AD=12,BD=5,
∴ AB2=AD2+BD2.
∴ 由勾股定理的逆定理得:△ABD是直角三角形,且∠ADB=90°.
∴∠ADC=90°.在Rt△ADC中,AC2=AD2+DC2.
∵AD=12,AC=15,
∴DC2=AC2-AD2=152-122=92.
∴ DC=9.
当堂检测
当堂检测
8.观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.根据你发现的规律,请写出:(1)当a=19时,b=________,c=________;
(2)当a=2n+1时,求b,c的值;
180
181
解:通过观察知c-b=1,
∵(2n+1)2+b2=c2,∴c2-b2=(2n+1)2,(b+c)(c-b)=(2n+1)2,∴b+c=(2n+1)2.又∵c=b+1,
∴2b+1=(2n+1)2,∴b=2n2+2n,c=2n2+2n+1.
当堂检测
(3)用(2)的结论判断15,111,112是否为一组勾股数,并说明理由.
解:不是.理由如下:由(2)知,2n+1,2n2+2n,2n2+2n+1为一组勾股数,当n=7时,2n+1=15,112-111=1,但2n2+2n=112≠111,∴15,111,112不是一组勾股数.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
