2023-2024学年人教版数学八年级上册11.1与三角形有关的线段 同步练习 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册11.1与三角形有关的线段 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 17:47:11 | ||
图片预览

文档简介
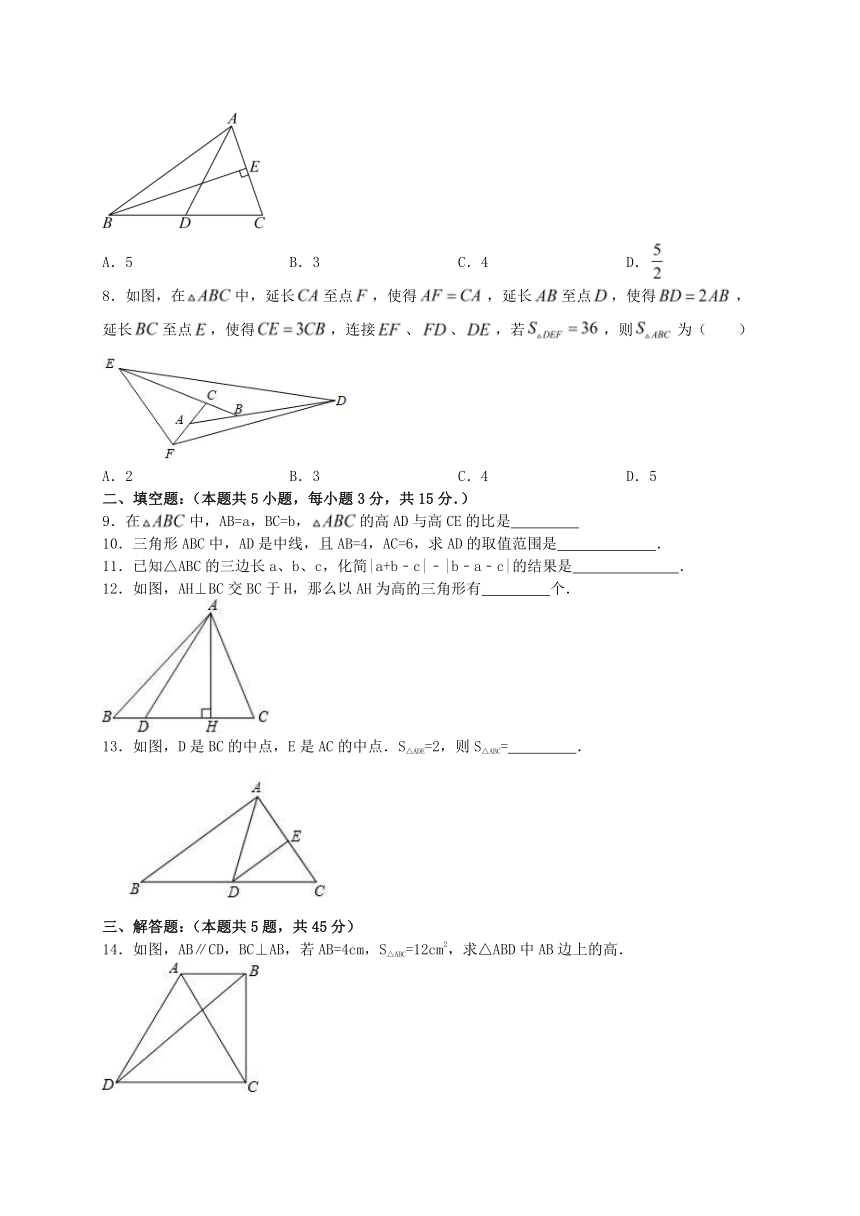
11.1与三角形有关的线段 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.能将一个三角形分成面积相等的两个三角形的一条线段是( )
A.三角形的角平分线 B.一个内角的平分线
C.三角形的高线 D.三角形的中线
2.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.13 B.10 C.3 D.2
3.有两根长度分别为4、9的木棒,若想钉一个三角形木架,现有五根长度分别为3,6,11,12,13的木棒供选择,则选择的方法有( ).
A.1种 B.2种 C.3种 D.4种
4.如图,在中,,则下列说法中,正确的是( )
A.是的中线 B.是的角平分线
C.是的高线 D.是的中线
5.如图,在 中, , , 为中线,则 与 的周长之差为( )
A.1 B.2 C.3 D.4
6.如图所示,在 ABC中,已知点D,E,F分别是BC,AD,CE的中点, =4,则 的值为( )
A.2 B.1 C.0.5 D.0.25
7.如图,,分别为的中线和高线,的面积为5,,则的长为( )
A.5 B.3 C.4 D.
8.如图,在中,延长至点,使得,延长至点,使得,延长至点,使得,连接、、,若,则为( )
A.2 B.3 C.4 D.5
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在中,AB=a,BC=b,的高AD与高CE的比是
10.三角形ABC中,AD是中线,且AB=4,AC=6,求AD的取值范围是 .
11.已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是 .
12.如图,AH⊥BC交BC于H,那么以AH为高的三角形有 个.
13.如图,D是BC的中点,E是AC的中点.S△ADE=2,则S△ABC= .
三、解答题:(本题共5题,共45分)
14.如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
15.如图,在中,平分,.若,,求的度数.
16.如图,在中,,点D是的中点,点E在上,,若,求的度数.
17.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
18.如图,ABC的面积为30,AD是ABC的中线,BE是ABD的中线,EF⊥BC于点F.
(1)求BDE的面积.
(2)若EF=5,求CD的长.
参考答案:
1.D 2.B 3.C 4.B 5.B 6.B 7.A 8.A
9.
10.1<AD<5
11.2(b﹣c)
12.6
13.8
14.解:S△ABC= AB BC= ×4 BC=12,
解得 BC=6,
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高等于6cm
15.解:如图:
平分
于点
.
16.解:∵,点D是的中点,
∴等腰三角形,则是的中线,是的角平分线,,
∵,
∴,
∵,
∴ ,
∴.
17.(1)解:∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,即
∴
∵AD是BC边上的中线,
∴.
(2)解:不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15cm<AB=18cm,
∴不能构成三角形ABC,
∴不能求出DC的长.
18.(1)解:∵AD是△ABC的中线,
∴.
∵BE是△ABD的中线,
∴.
(2)解:∵EF⊥BC,
∴,即.
∴BD=3.
∵AD是△ABC的中线,
∴CD=BD=3
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.能将一个三角形分成面积相等的两个三角形的一条线段是( )
A.三角形的角平分线 B.一个内角的平分线
C.三角形的高线 D.三角形的中线
2.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.13 B.10 C.3 D.2
3.有两根长度分别为4、9的木棒,若想钉一个三角形木架,现有五根长度分别为3,6,11,12,13的木棒供选择,则选择的方法有( ).
A.1种 B.2种 C.3种 D.4种
4.如图,在中,,则下列说法中,正确的是( )
A.是的中线 B.是的角平分线
C.是的高线 D.是的中线
5.如图,在 中, , , 为中线,则 与 的周长之差为( )
A.1 B.2 C.3 D.4
6.如图所示,在 ABC中,已知点D,E,F分别是BC,AD,CE的中点, =4,则 的值为( )
A.2 B.1 C.0.5 D.0.25
7.如图,,分别为的中线和高线,的面积为5,,则的长为( )
A.5 B.3 C.4 D.
8.如图,在中,延长至点,使得,延长至点,使得,延长至点,使得,连接、、,若,则为( )
A.2 B.3 C.4 D.5
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在中,AB=a,BC=b,的高AD与高CE的比是
10.三角形ABC中,AD是中线,且AB=4,AC=6,求AD的取值范围是 .
11.已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是 .
12.如图,AH⊥BC交BC于H,那么以AH为高的三角形有 个.
13.如图,D是BC的中点,E是AC的中点.S△ADE=2,则S△ABC= .
三、解答题:(本题共5题,共45分)
14.如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
15.如图,在中,平分,.若,,求的度数.
16.如图,在中,,点D是的中点,点E在上,,若,求的度数.
17.已知△ABC的周长为33cm,AD是BC边上的中线,.
(1)如图,当AC=10cm时,求BD的长.
(2)若AC=12cm,能否求出DC的长?为什么?
18.如图,ABC的面积为30,AD是ABC的中线,BE是ABD的中线,EF⊥BC于点F.
(1)求BDE的面积.
(2)若EF=5,求CD的长.
参考答案:
1.D 2.B 3.C 4.B 5.B 6.B 7.A 8.A
9.
10.1<AD<5
11.2(b﹣c)
12.6
13.8
14.解:S△ABC= AB BC= ×4 BC=12,
解得 BC=6,
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高等于6cm
15.解:如图:
平分
于点
.
16.解:∵,点D是的中点,
∴等腰三角形,则是的中线,是的角平分线,,
∵,
∴,
∵,
∴ ,
∴.
17.(1)解:∵,AC=10cm,
∴AB=15cm.
又∵△ABC的周长是33cm,即
∴
∵AD是BC边上的中线,
∴.
(2)解:不能,理由如下:
∵,AC=12cm,
∴AB=18cm.
又∵△ABC的周长是33cm,
∴BC=3cm.
∵AC+BC=15cm<AB=18cm,
∴不能构成三角形ABC,
∴不能求出DC的长.
18.(1)解:∵AD是△ABC的中线,
∴.
∵BE是△ABD的中线,
∴.
(2)解:∵EF⊥BC,
∴,即.
∴BD=3.
∵AD是△ABC的中线,
∴CD=BD=3
