2023-2024学年人教版数学八年级上册11.2与三角形有关的角 同步练习 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册11.2与三角形有关的角 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 183.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 17:49:09 | ||
图片预览


文档简介
11.2与三角形有关的角 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.Rt△ABC中,∠C=90°,∠B=54°,则∠A的度数是( )
A.66° B.36° C.56° D.46°
2.△ABC中,∠A=40°,高BD和CE交于O,则∠COD为( )
A.40°或140° B.50°或130° C.40° D.50°
3.如图,直线AB∥CD,∠M=90°,∠C=120°,则∠MPB=( )
A.30° B.60° C.120° D.150°
4.如图,射线AD,BE,CF构成∠1,∠2,∠3,则∠1+∠2+∠3=( )
A.180° B.360° C.540° D.无法确定
5.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是( )
A.70° B.44° C.34° D.24°
6.如图,在 中, , , 平分 ,则 的度数为( )
A.80° B.85° C.90° D.95°
7.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A.2∠A=∠2﹣∠1 B.3∠A=2(∠2﹣∠1)
C.3∠A=2∠1﹣∠2 D.∠A=∠2﹣∠1
8.如图,BD平分,点E,F分别在BA和BC上,EG平分交BD于点G,.下列结论:①;②;③;④,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.②④
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在△ABC中,若∠A:∠B:∠C=1:2:3,则∠B= .
10.已知在△ABC中,∠A=40°,∠B-∠C=40°,则∠B= ,∠C= .
11.如图,已知AE∥BD,∠1=3∠2,∠2=38°.求∠C= °.
12.AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB= .
13.如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连接NE、NM,过点N作NG平分∠ENM,交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF= 度.
三、解答题:(本题共5题,共45分)
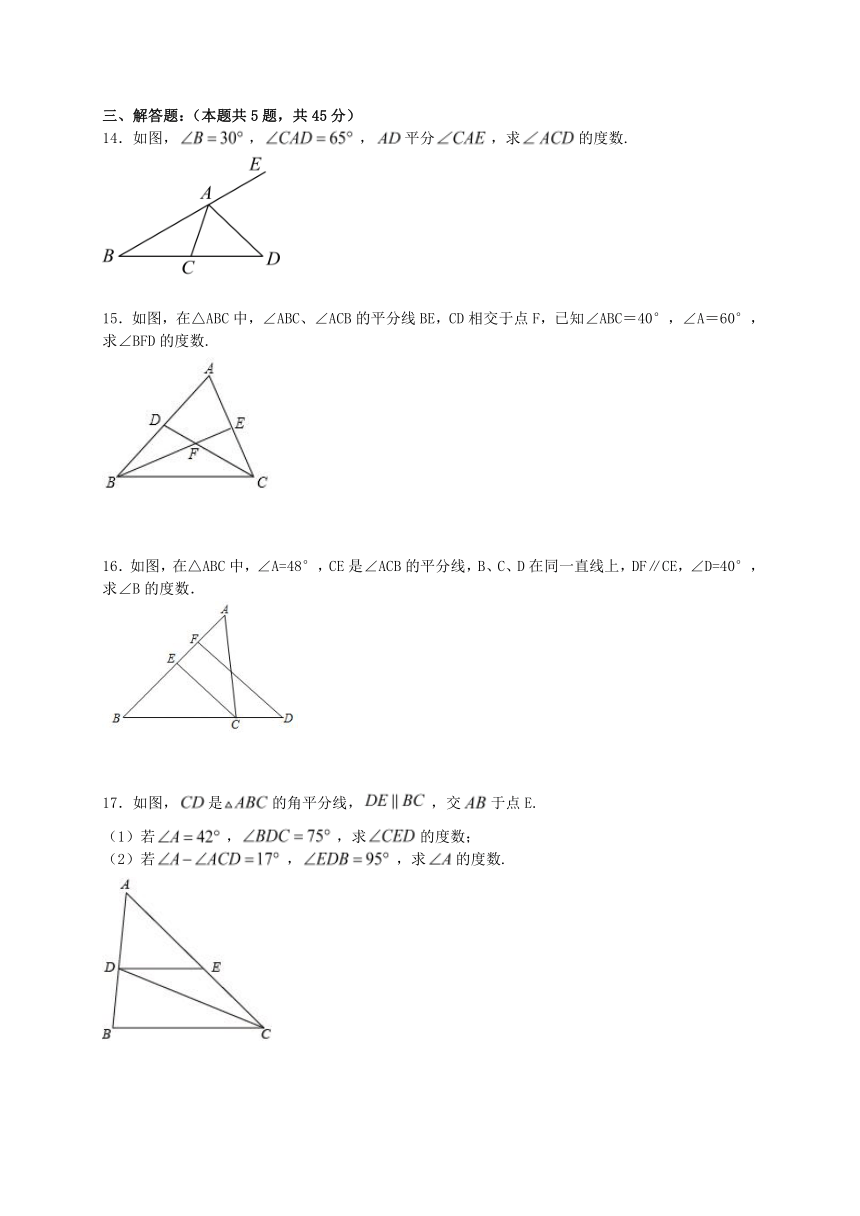
14.如图,,,平分,求的度数.
15.如图,在△ABC中,∠ABC、∠ACB的平分线BE,CD相交于点F,已知∠ABC=40°,∠A=60°,求∠BFD的度数.
16.如图,在△ABC中,∠A=48°,CE是∠ACB的平分线,B、C、D在同一直线上,DF∥CE,∠D=40°,求∠B的度数.
17.如图,是的角平分线,,交于点E.
(1)若,,求的度数;
(2)若,,求的度数.
18.如图,已知,在 中, 平分 交 于点 分别在 的延长线上,
(1)求证:
(2)若 比 大 ,求 的度数.
参考答案:
1.B 2.C 3.D 4.B 5.C 6.B 7.A 8.C
9.60°
10.90°;50°
11.76
12.26°
13.110
14.解:,平分,
,
,
,
.
15.解:∵∠A=60°
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)=60°,
∵∠BFD=∠FBC+∠FCB,
∴∠BFD=60°.
16.解:DF∥CE,
∴∠ECB=∠D=40°.
∵CE是∠ACB的平分线,
∴∠ACE=∠ECB=40°,
∴∠ACB=80°.
在△ABC中,∠A+∠B+∠ACB=180°,
∴∠B=180°-∠A-∠ACB=180°-48°-80°=52°
17.(1)解:设,
∵平分,∴,
∵,∴,
∵,∴,解之得:,
∴,
∵,
∴,
∴,
(2)解:∵,,
∴,
设,则
∵,
∴,解之得:,
∴
18.(1)证明:∵DB AH,
∴∠D=∠CAH,
∵AH平分∠BAC,
∴∠BAH=∠CAH,
∵∠D=∠E,
∴∠BAH=∠E,
∴AH∥EC,
∴DB EC;
(2)解:设∠ABC=x,则∠ABD=2x,则∠BAH=2x,则∠DAB=180° 4x,则∠AHC=168° 4x,依题意有
168° 4x=3x,
解得x=24°,
则∠D=∠CAH=∠BAH=∠ABD=2x=48°
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.Rt△ABC中,∠C=90°,∠B=54°,则∠A的度数是( )
A.66° B.36° C.56° D.46°
2.△ABC中,∠A=40°,高BD和CE交于O,则∠COD为( )
A.40°或140° B.50°或130° C.40° D.50°
3.如图,直线AB∥CD,∠M=90°,∠C=120°,则∠MPB=( )
A.30° B.60° C.120° D.150°
4.如图,射线AD,BE,CF构成∠1,∠2,∠3,则∠1+∠2+∠3=( )
A.180° B.360° C.540° D.无法确定
5.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是( )
A.70° B.44° C.34° D.24°
6.如图,在 中, , , 平分 ,则 的度数为( )
A.80° B.85° C.90° D.95°
7.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A.2∠A=∠2﹣∠1 B.3∠A=2(∠2﹣∠1)
C.3∠A=2∠1﹣∠2 D.∠A=∠2﹣∠1
8.如图,BD平分,点E,F分别在BA和BC上,EG平分交BD于点G,.下列结论:①;②;③;④,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.②④
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在△ABC中,若∠A:∠B:∠C=1:2:3,则∠B= .
10.已知在△ABC中,∠A=40°,∠B-∠C=40°,则∠B= ,∠C= .
11.如图,已知AE∥BD,∠1=3∠2,∠2=38°.求∠C= °.
12.AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB= .
13.如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连接NE、NM,过点N作NG平分∠ENM,交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF= 度.
三、解答题:(本题共5题,共45分)
14.如图,,,平分,求的度数.
15.如图,在△ABC中,∠ABC、∠ACB的平分线BE,CD相交于点F,已知∠ABC=40°,∠A=60°,求∠BFD的度数.
16.如图,在△ABC中,∠A=48°,CE是∠ACB的平分线,B、C、D在同一直线上,DF∥CE,∠D=40°,求∠B的度数.
17.如图,是的角平分线,,交于点E.
(1)若,,求的度数;
(2)若,,求的度数.
18.如图,已知,在 中, 平分 交 于点 分别在 的延长线上,
(1)求证:
(2)若 比 大 ,求 的度数.
参考答案:
1.B 2.C 3.D 4.B 5.C 6.B 7.A 8.C
9.60°
10.90°;50°
11.76
12.26°
13.110
14.解:,平分,
,
,
,
.
15.解:∵∠A=60°
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)=60°,
∵∠BFD=∠FBC+∠FCB,
∴∠BFD=60°.
16.解:DF∥CE,
∴∠ECB=∠D=40°.
∵CE是∠ACB的平分线,
∴∠ACE=∠ECB=40°,
∴∠ACB=80°.
在△ABC中,∠A+∠B+∠ACB=180°,
∴∠B=180°-∠A-∠ACB=180°-48°-80°=52°
17.(1)解:设,
∵平分,∴,
∵,∴,
∵,∴,解之得:,
∴,
∵,
∴,
∴,
(2)解:∵,,
∴,
设,则
∵,
∴,解之得:,
∴
18.(1)证明:∵DB AH,
∴∠D=∠CAH,
∵AH平分∠BAC,
∴∠BAH=∠CAH,
∵∠D=∠E,
∴∠BAH=∠E,
∴AH∥EC,
∴DB EC;
(2)解:设∠ABC=x,则∠ABD=2x,则∠BAH=2x,则∠DAB=180° 4x,则∠AHC=168° 4x,依题意有
168° 4x=3x,
解得x=24°,
则∠D=∠CAH=∠BAH=∠ABD=2x=48°
