第二十二章 二次函数 单元测试(含答案)人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数 单元测试(含答案)人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 376.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 19:39:33 | ||
图片预览



文档简介
第二十二章 二次函数 单元练习 2022-2023学年人教版数学九年级上册
一、选择题
1.抛物线 与坐标轴的交点个数是
A. B. C. D.
2.若一次函数 的图象与 轴的交点坐标为 ,则抛物线 的对称轴为
A.直线 B.直线 C.直线 D.直线
3.已知学校航模组设计制作的火箭的升空高度 与飞行时间 满足函数表达式 .则下列说法中正确的是
A.点火后 和点火后 的升空高度相同
B.点火后 火箭落于地面
C.点火后 的升空高度为
D.火箭升空的最大高度为
4.点 , 是抛物线 上的点,则 , 的大小关系为
A. B. C. D.无法确定
5.如图是抛物线 的大致图象,则一元二次方程
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
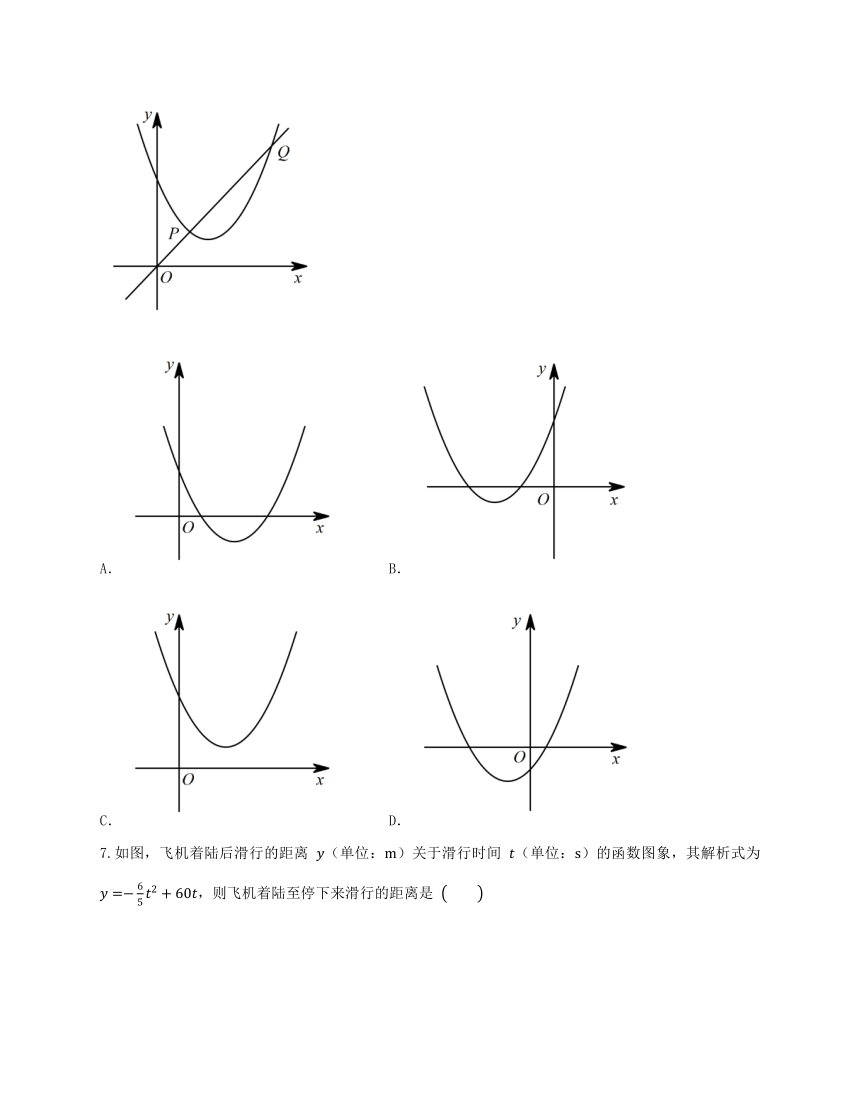
6.如图,一次函数 与二次函数 图象相交于 、 两点,则函数 的图象可能是
A. B.
C. D.
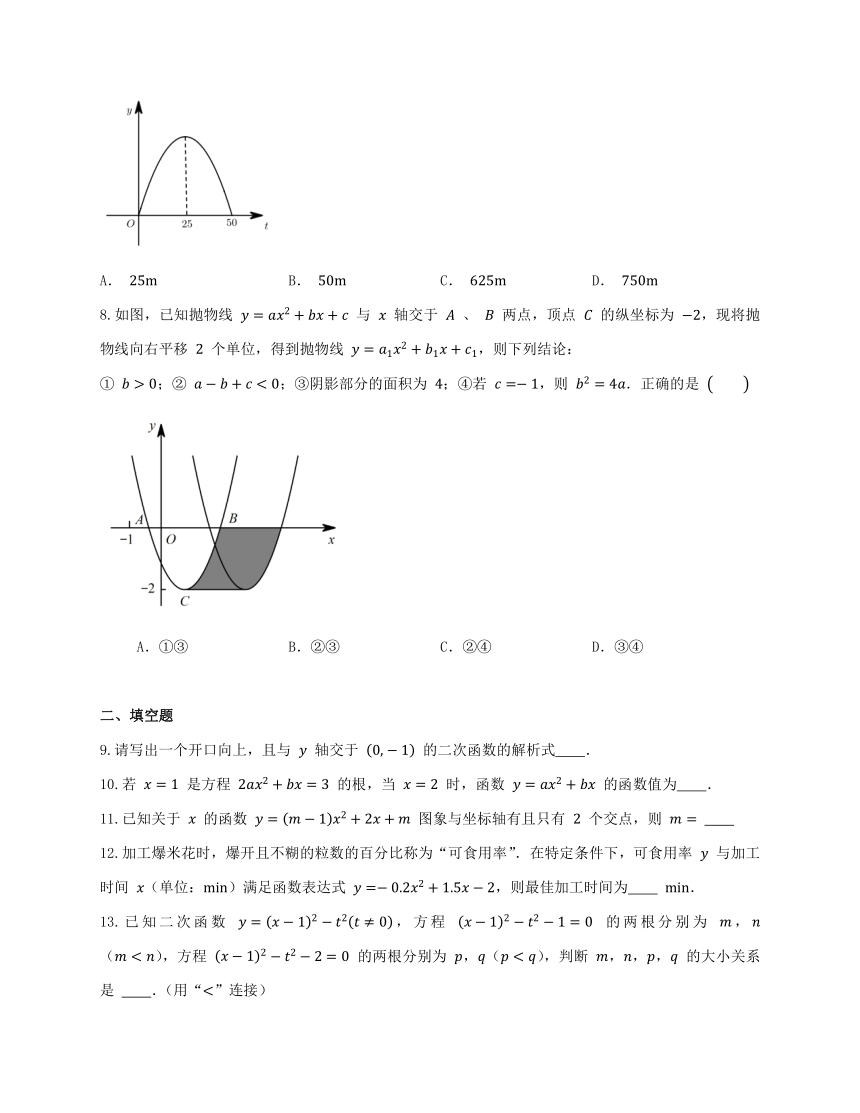
7.如图,飞机着陆后滑行的距离 (单位:)关于滑行时间 (单位:)的函数图象,其解析式为 ,则飞机着陆至停下来滑行的距离是
A. B. C. D.
8.如图,已知抛物线 与 轴交于 、 两点,顶点 的纵坐标为 ,现将抛物线向右平移 个单位,得到抛物线 ,则下列结论:
① ;② ;③阴影部分的面积为 ;④若 ,则 .正确的是
A.①③ B.②③ C.②④ D.③④
二、填空题
9.请写出一个开口向上,且与 轴交于 的二次函数的解析式 .
10.若 是方程 的根,当 时,函数 的函数值为 .
11.已知关于 的函数 图象与坐标轴有且只有 个交点,则
12.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位:)满足函数表达式 ,则最佳加工时间为 .
13.已知二次函数 ,方程 的两根分别为 ,(),方程 的两根分别为 ,(),判断 ,,, 的大小关系是 .(用“”连接)
三、解答题
14.如图,直线 是一次函数 的图象.
(1) 求出这个一次函数的解析式.
(2) 将该函数的图象向下平移 个单位,求出平移后一次函数的解析式,并写出平移后的图象与 轴的交点坐标.
15.某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润 (万元)与时间 (月)之间的关系(即前 个月的利润总和 与 之间的关系).根据图象提供的信息,解答下列问题:
(1) 求累积利润 (万元)与时间 (月)之间的函数关系式.
(2) 求截止到几月末公司累积利润可达 万元.
(3) 求第 个月公司所获利润是多少万元?
16.如图,在平面直角坐标系中, 为坐标原点,二次函数 的图象与 轴交于 , 两点, 点坐标为 与 轴交于点 .
(1) 求这个二次函数的解析式.
(2) 设这个二次函数的图象的顶点为 ,求 的面积.
(3) 若方程 有两个不相等的实数根,则 的取值范围是 .
17.某商店原来平均每天可销售某种水果 千克,每千克可盈利 元,为减少库存,经市场调查,如果这种水果每千克降价 元,则每天可所多售出 千克.
(1) 设每千克水果降价 元,平均每天盈利 元,试写出 关于 的函数表达式;
(2) 若要平均每天盈利 元,则每千克应降价多少元?
(3) 每千克降价多少元时,每天的盈利最多?最多盈利多少元?
18.如图,抛物线 交 轴正半轴于点 ,直线 经过抛物线的顶点 .已知该抛物线的对称轴为直线 ,交 轴于点 .
(1) 求 , 的值.
(2) 是第一象限内抛物线上的一点,且在对称轴的右侧,连接 ,.设点 的横坐标为 , 的面积为 ,记 .求 关于 的函数表达式及 的范围.
19.在平面直角坐标系 中,抛物线 ,与 轴交于点 ,(点 在点 的左侧),与 轴交于点 .
(1) 求抛物线顶点 的坐标.
(2) 若点 的坐标为 , 轴,交抛物线于点 ,求点 的坐标.
(3) 在()的条件下,将抛物线在 , 两点之间的部分沿 轴翻折,翻折后的图象记为 ,若直线 与图象 有一个交点,结合函数的图象,求 的取值范围.
参考答案
1. C
2. C
3. D
4. A
5. A
6. A
7. D
8. D
9. ,答案不唯一
10.
11. ,,,
12.
13. 14. (1) 一次函数 的图象经过点 和点 ,
解得 ,,
一次函数的解析式为:.
(2) 一次函数 向下平移 个单位的解析式为 ,
当 时,,
平移后的图象与 轴的交点坐标为 .
15. (1) 由图象可知: 与 函数图象的顶点坐标为 ,过点 ,
设: 与 间的函数关系为 .
将点 代入,得:,
与 之间的函数关系式为:.
(2) 令 ,
得:,
解得 ,(舍去).
截止到 月末公司累积利润可达 万元.
(3) 令 ,,
令 ,.
第 个月所获利润为 万元.
16. (1) 将 , 代入,
得 解得
二次函数解析式为:.
(2) 由()知 ,配方,得 ,
顶点 的坐标为 .
另 ,,解得 ,
点 的坐标为 .
又 点 坐标为 ,
.
(3)
17. (1) 根据题意得:
(2) 令 中 ,则有:,
即 ,
解得:(舍去),.
所以若要平均每天盈利 元,则每千克应降价 元.
(3) ,
所以每千克降价 元时,每天的盈利最多,最多盈利多, 元.
18. (1) 将 代入 得 .
.
由题意得
(2) 如图,过点 作 轴于点 .
点 的横坐标为 ,抛物线的函数表达式为 ,
.
,
.
.
由题意得 ,
,
.
随着 的增大而减小,
.
19. (1) .
(2) .
(3) 抛物线 与 轴交于点 ,
.
.
抛物线的表达式为 .
由 .
由 ,得:.
抛物线 与 轴的交点 的坐标为 ,
点 关于 轴的对称点 的坐标为 .
把 代入 ,得:.
把 代入 ,得:.
所求 的取值范围是 或 .
一、选择题
1.抛物线 与坐标轴的交点个数是
A. B. C. D.
2.若一次函数 的图象与 轴的交点坐标为 ,则抛物线 的对称轴为
A.直线 B.直线 C.直线 D.直线
3.已知学校航模组设计制作的火箭的升空高度 与飞行时间 满足函数表达式 .则下列说法中正确的是
A.点火后 和点火后 的升空高度相同
B.点火后 火箭落于地面
C.点火后 的升空高度为
D.火箭升空的最大高度为
4.点 , 是抛物线 上的点,则 , 的大小关系为
A. B. C. D.无法确定
5.如图是抛物线 的大致图象,则一元二次方程
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
6.如图,一次函数 与二次函数 图象相交于 、 两点,则函数 的图象可能是
A. B.
C. D.
7.如图,飞机着陆后滑行的距离 (单位:)关于滑行时间 (单位:)的函数图象,其解析式为 ,则飞机着陆至停下来滑行的距离是
A. B. C. D.
8.如图,已知抛物线 与 轴交于 、 两点,顶点 的纵坐标为 ,现将抛物线向右平移 个单位,得到抛物线 ,则下列结论:
① ;② ;③阴影部分的面积为 ;④若 ,则 .正确的是
A.①③ B.②③ C.②④ D.③④
二、填空题
9.请写出一个开口向上,且与 轴交于 的二次函数的解析式 .
10.若 是方程 的根,当 时,函数 的函数值为 .
11.已知关于 的函数 图象与坐标轴有且只有 个交点,则
12.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位:)满足函数表达式 ,则最佳加工时间为 .
13.已知二次函数 ,方程 的两根分别为 ,(),方程 的两根分别为 ,(),判断 ,,, 的大小关系是 .(用“”连接)
三、解答题
14.如图,直线 是一次函数 的图象.
(1) 求出这个一次函数的解析式.
(2) 将该函数的图象向下平移 个单位,求出平移后一次函数的解析式,并写出平移后的图象与 轴的交点坐标.
15.某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润 (万元)与时间 (月)之间的关系(即前 个月的利润总和 与 之间的关系).根据图象提供的信息,解答下列问题:
(1) 求累积利润 (万元)与时间 (月)之间的函数关系式.
(2) 求截止到几月末公司累积利润可达 万元.
(3) 求第 个月公司所获利润是多少万元?
16.如图,在平面直角坐标系中, 为坐标原点,二次函数 的图象与 轴交于 , 两点, 点坐标为 与 轴交于点 .
(1) 求这个二次函数的解析式.
(2) 设这个二次函数的图象的顶点为 ,求 的面积.
(3) 若方程 有两个不相等的实数根,则 的取值范围是 .
17.某商店原来平均每天可销售某种水果 千克,每千克可盈利 元,为减少库存,经市场调查,如果这种水果每千克降价 元,则每天可所多售出 千克.
(1) 设每千克水果降价 元,平均每天盈利 元,试写出 关于 的函数表达式;
(2) 若要平均每天盈利 元,则每千克应降价多少元?
(3) 每千克降价多少元时,每天的盈利最多?最多盈利多少元?
18.如图,抛物线 交 轴正半轴于点 ,直线 经过抛物线的顶点 .已知该抛物线的对称轴为直线 ,交 轴于点 .
(1) 求 , 的值.
(2) 是第一象限内抛物线上的一点,且在对称轴的右侧,连接 ,.设点 的横坐标为 , 的面积为 ,记 .求 关于 的函数表达式及 的范围.
19.在平面直角坐标系 中,抛物线 ,与 轴交于点 ,(点 在点 的左侧),与 轴交于点 .
(1) 求抛物线顶点 的坐标.
(2) 若点 的坐标为 , 轴,交抛物线于点 ,求点 的坐标.
(3) 在()的条件下,将抛物线在 , 两点之间的部分沿 轴翻折,翻折后的图象记为 ,若直线 与图象 有一个交点,结合函数的图象,求 的取值范围.
参考答案
1. C
2. C
3. D
4. A
5. A
6. A
7. D
8. D
9. ,答案不唯一
10.
11. ,,,
12.
13. 14. (1) 一次函数 的图象经过点 和点 ,
解得 ,,
一次函数的解析式为:.
(2) 一次函数 向下平移 个单位的解析式为 ,
当 时,,
平移后的图象与 轴的交点坐标为 .
15. (1) 由图象可知: 与 函数图象的顶点坐标为 ,过点 ,
设: 与 间的函数关系为 .
将点 代入,得:,
与 之间的函数关系式为:.
(2) 令 ,
得:,
解得 ,(舍去).
截止到 月末公司累积利润可达 万元.
(3) 令 ,,
令 ,.
第 个月所获利润为 万元.
16. (1) 将 , 代入,
得 解得
二次函数解析式为:.
(2) 由()知 ,配方,得 ,
顶点 的坐标为 .
另 ,,解得 ,
点 的坐标为 .
又 点 坐标为 ,
.
(3)
17. (1) 根据题意得:
(2) 令 中 ,则有:,
即 ,
解得:(舍去),.
所以若要平均每天盈利 元,则每千克应降价 元.
(3) ,
所以每千克降价 元时,每天的盈利最多,最多盈利多, 元.
18. (1) 将 代入 得 .
.
由题意得
(2) 如图,过点 作 轴于点 .
点 的横坐标为 ,抛物线的函数表达式为 ,
.
,
.
.
由题意得 ,
,
.
随着 的增大而减小,
.
19. (1) .
(2) .
(3) 抛物线 与 轴交于点 ,
.
.
抛物线的表达式为 .
由 .
由 ,得:.
抛物线 与 轴的交点 的坐标为 ,
点 关于 轴的对称点 的坐标为 .
把 代入 ,得:.
把 代入 ,得:.
所求 的取值范围是 或 .
同课章节目录
