1.5.3近似数 课件(共24张PPT)
文档属性
| 名称 | 1.5.3近似数 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 15:22:41 | ||
图片预览








文档简介
(共24张PPT)
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第一章有理数
1.5.3近似数
学习目标
1.理解近似数及其精确度的意义.
2.能够准确地说出精确数位,以及用四舍五入取近似数.
复习提问
对于参加同一个会议的人数,有两个报道:
一个报道说:“会议秘书处宣布,参加今天会议的有513人.”
另一个报道说:“约有五百人参加了今天的会议.”
这里数字513确切地反应了实际人数,它是一个准确数.
五百这个数只是接近实际人数,但与实际人数还有差别,它是一个近似数.
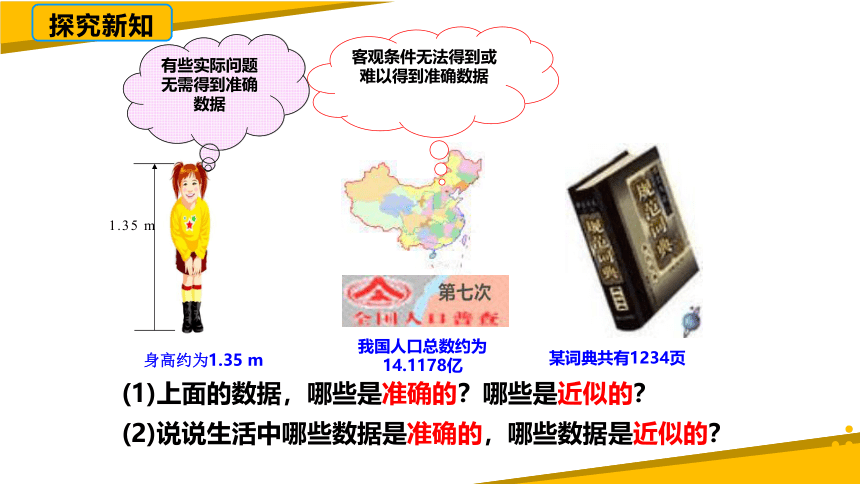
探究新知
我国人口总数约为14.1178亿
某词典共有1234页
(1)上面的数据,哪些是准确的?哪些是近似的?
客观条件无法得到或难以得到准确数据
(2)说说生活中哪些数据是准确的,哪些数据是近似的?
1.35 m
有些实际问题无需得到准确数据
身高约为1.35 m
探究新知
1. 什么叫准确数?
2. 什么叫近似数?
与实际完全符合的数.
与实际非常接近的数.
探究新知
在许多情况下,很难取得准确数,或者不必使用准确数,而可以使用近似数.
例如:宇宙现在的年龄约为200亿年
长江长约6300千米
圆周率π为3.14
近似数与准确数的接近程度,可以用精确度表示.
例如,前面的五百是精确到百位的近似数,它与准确数513的误差为13.
探究新知
按四舍五入法对圆周率π取近似数时,有
π≈ 3 (精确到_________)
π≈3.1 (精确到_______或叫做精确到_________ )
π≈3.14 (精确到_________或叫做精确到________ )
π≈3.142 (精确到_______或叫做精确到_________)
π≈3.1416(精确到________或叫做精确到_______)
……
个位
0.1
十分位
0.01
百分位
0.001
千分位
0.0001
万分位
探究新知
近似数是一个与准确数接近的数,其接近程度可以用精确度表示.
表示一个近似数近似的程度.
什么叫精确度?
利用四舍五入法得到的近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.
例如前面的五百是精确到百位的近似数,与准确数513的误差为13.
典例解析
解:(1) 0.015 8≈0.016;
(2)304.35≈304;
(3)1.804≈1.8;
(4)1.804≈1.80.
例6 按括号内的要求,用四舍五入法对下列各数取近似数:
(1)0.015 8 (精确到 0.001); (2)304.35 (精确到个位);
(3)1.804 (精确到 0.1); (4)1.804 (精确到 0.01).
这里的1.8和 1.80的精确度相同吗?表示近似数时,能简单地把1.80后面的0去掉吗?
典例解析
找不同点
解:有效数字不同 :
1.80有三个有效数字,
1.8有二个有效数字.
精确度不同:
1.80精确到百分位,
1.8 精确到十分位.
近似数
1.80
1.8
由此可见,1.80比1.8的精确度高.
典例解析
例7:下列由四舍五入得到的近似数,各精确到哪一位?
(1) 600万 ; (2) 7.03万;
(3) 5.8亿 ; (4) 3.30×105.
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
先把数还原,再看3所在的数位
随堂练习
1.用四舍五入法对下列各数取近似数:
(1) 0.00356 (精确到万分位) (2) 61.235 (精确到个位)
(3) 1.8935 (精确到0.001) (4) 0.0571 (精确到0.1)
随堂练习
2. 下列结论正确的是 ( )
A.近似数4.230和4.23的精确度是一样的
B.近似数89.0是精确到个位
C.近似数0.00510与0.0510的精确度不一样
D.近似数6万与近似数60 000的精确度相同
C
随堂练习
3. 小红量得课桌长为1.025m,用四舍五入法按下列要求取这个数的近似数:
(1) 精确到0.01;
(2) 精确到十分位;
(3) 精确到个位.
(1) 1.025 m精确到0.01是1.03 m;
(2) 1.025 m精确到十分位是1.0 m;
(3) 1.025 m精确到个位是1 m.
近似数1.0后面的0能去掉吗?
近似数1和1.0
精确度相同吗?
解:
随堂练习
(1) 保留整数
即精确到十分位(或精确到0.1);
即精确到百分位(或精确到0.01).
(2) 保留一位小数
(3) 保留两位小数
即精确到个位;
中考链接
中考链接
课堂小结
1.准确数——与实际完全符合的数.
2.近似数——与实际接近的数.
3.精确度——表示一个近似数与准确数接近的程度.
4. 精确度的两种形式:
(1)精确到个位,十分位,百分位…;
(2)精确到1,0.1,0.01 … .
5. 近似数的表示方法:
先根据要求,找准所在位的数字,再把这个数字后面的数字四舍五入.
当堂测试
当堂测试
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第一章有理数
1.5.3近似数
学习目标
1.理解近似数及其精确度的意义.
2.能够准确地说出精确数位,以及用四舍五入取近似数.
复习提问
对于参加同一个会议的人数,有两个报道:
一个报道说:“会议秘书处宣布,参加今天会议的有513人.”
另一个报道说:“约有五百人参加了今天的会议.”
这里数字513确切地反应了实际人数,它是一个准确数.
五百这个数只是接近实际人数,但与实际人数还有差别,它是一个近似数.
探究新知
我国人口总数约为14.1178亿
某词典共有1234页
(1)上面的数据,哪些是准确的?哪些是近似的?
客观条件无法得到或难以得到准确数据
(2)说说生活中哪些数据是准确的,哪些数据是近似的?
1.35 m
有些实际问题无需得到准确数据
身高约为1.35 m
探究新知
1. 什么叫准确数?
2. 什么叫近似数?
与实际完全符合的数.
与实际非常接近的数.
探究新知
在许多情况下,很难取得准确数,或者不必使用准确数,而可以使用近似数.
例如:宇宙现在的年龄约为200亿年
长江长约6300千米
圆周率π为3.14
近似数与准确数的接近程度,可以用精确度表示.
例如,前面的五百是精确到百位的近似数,它与准确数513的误差为13.
探究新知
按四舍五入法对圆周率π取近似数时,有
π≈ 3 (精确到_________)
π≈3.1 (精确到_______或叫做精确到_________ )
π≈3.14 (精确到_________或叫做精确到________ )
π≈3.142 (精确到_______或叫做精确到_________)
π≈3.1416(精确到________或叫做精确到_______)
……
个位
0.1
十分位
0.01
百分位
0.001
千分位
0.0001
万分位
探究新知
近似数是一个与准确数接近的数,其接近程度可以用精确度表示.
表示一个近似数近似的程度.
什么叫精确度?
利用四舍五入法得到的近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.
例如前面的五百是精确到百位的近似数,与准确数513的误差为13.
典例解析
解:(1) 0.015 8≈0.016;
(2)304.35≈304;
(3)1.804≈1.8;
(4)1.804≈1.80.
例6 按括号内的要求,用四舍五入法对下列各数取近似数:
(1)0.015 8 (精确到 0.001); (2)304.35 (精确到个位);
(3)1.804 (精确到 0.1); (4)1.804 (精确到 0.01).
这里的1.8和 1.80的精确度相同吗?表示近似数时,能简单地把1.80后面的0去掉吗?
典例解析
找不同点
解:有效数字不同 :
1.80有三个有效数字,
1.8有二个有效数字.
精确度不同:
1.80精确到百分位,
1.8 精确到十分位.
近似数
1.80
1.8
由此可见,1.80比1.8的精确度高.
典例解析
例7:下列由四舍五入得到的近似数,各精确到哪一位?
(1) 600万 ; (2) 7.03万;
(3) 5.8亿 ; (4) 3.30×105.
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
先把数还原,再看3所在的数位
随堂练习
1.用四舍五入法对下列各数取近似数:
(1) 0.00356 (精确到万分位) (2) 61.235 (精确到个位)
(3) 1.8935 (精确到0.001) (4) 0.0571 (精确到0.1)
随堂练习
2. 下列结论正确的是 ( )
A.近似数4.230和4.23的精确度是一样的
B.近似数89.0是精确到个位
C.近似数0.00510与0.0510的精确度不一样
D.近似数6万与近似数60 000的精确度相同
C
随堂练习
3. 小红量得课桌长为1.025m,用四舍五入法按下列要求取这个数的近似数:
(1) 精确到0.01;
(2) 精确到十分位;
(3) 精确到个位.
(1) 1.025 m精确到0.01是1.03 m;
(2) 1.025 m精确到十分位是1.0 m;
(3) 1.025 m精确到个位是1 m.
近似数1.0后面的0能去掉吗?
近似数1和1.0
精确度相同吗?
解:
随堂练习
(1) 保留整数
即精确到十分位(或精确到0.1);
即精确到百分位(或精确到0.01).
(2) 保留一位小数
(3) 保留两位小数
即精确到个位;
中考链接
中考链接
课堂小结
1.准确数——与实际完全符合的数.
2.近似数——与实际接近的数.
3.精确度——表示一个近似数与准确数接近的程度.
4. 精确度的两种形式:
(1)精确到个位,十分位,百分位…;
(2)精确到1,0.1,0.01 … .
5. 近似数的表示方法:
先根据要求,找准所在位的数字,再把这个数字后面的数字四舍五入.
当堂测试
当堂测试
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
