贵州省黔南布依族苗族自治州长顺县2022-2023学年八年级下学期期末数学试题(含答案)
文档属性
| 名称 | 贵州省黔南布依族苗族自治州长顺县2022-2023学年八年级下学期期末数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 391.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 00:00:00 | ||
图片预览




文档简介
2022-2023学年第二学期学业水平监测
八年级数学
注意事项:
1.共三个大题,满分100分,时间120分钟;
2.请用黑墨水的钢笔或水性笔在答题卡上作答,选择题在答题卡上用2B铅笔作答。
一、选择题(本大题共12小题,每小题2分,共24分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)
1.下列实数中,比大的数是()
A.1 B. C.2 D.
2.如图,在中,∠A=125°,则∠1=()
A.65° B.50° C.55° D.45°
3.下列长度的线段不能构成直角三角形的是()
A.3,4,5 B.5,12,13 C.1,2,3 D.6,8,10
4.若式子在实数范围内有意义,则x的取值范围是()
A.x≥2 B.x>2 C.x<2 D.x≤2
5.菱形两条对角线长为12cm和16cm,则菱形周长为()cm.
A.24 B.40 C.32 D.42
6.下列计算正确的是()
A. B.
C. D.
7.对于函数y=12x-4,下列结论正确的是()
A.y的值随x值的增大而减小 B.它的图象经过第一、二、三象限
C.当时,y>0 D.它的图象必经过点(-4,0)
8.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3和S4.若S1=2,S2=8,S4=3,则S3的值是()
A.8 B.7 C.6 D.5
9.我校英语兴趣小组20名学生某日记单词数量如下表所示:
单词数量/个 6 810 12 14
人数/人 3 2 5 6 2
这些学生某日记单词数量的中位数、众数分别是()
A.8,10 B.10,12 C.5,6 D.8,12
10.如图,长方形ABCD的顶点A,B在数轴上,点A表示-1,AB=3,AD=1.若以点A为圆心,对角线AC长为半径作弧,交数轴正半轴于点M,则点M所表示的数为()
A. B. C. D.
11.如图,在长方形ABCD中,点E是CD上一点,连接AE,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.若AB=9,CE=4,则折痕AE的长度为()
A. B. C. D.
12.某学校准备购买一批作业本,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费,甲、乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图分别如图中甲、乙所示,下列三种说法:
①甲厂的制版费为1千元;
②当印制作业本超过2千个时,乙厂的印刷费用为0.2元/个;
③当印制作业本8千个时,应选择乙厂,可节省费用500元。
其中正确的说法有()
A.①② B.②③ C.①③ D.①②③
二、填空题(本大题共4小题,每小题3分,共12分)
13.计算的结果是__________.
14.在一次“一分钟跳绳”比赛中,甲、乙两人各跳三轮,两人三次跳绳个数的平均数均是182个,他们成绩的方差分别记为,,若甲、乙两人在这三轮比赛中乙成绩更稳定,那么,的大小关系是_________(填“>”,“<”,“=”)
15.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为__________.
16.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是__________.
三、解答题(本大题共9小题,共64分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(5分)计算
18.(6分)先化简,再求值:,其中
19.(6分)如图,在平行四边形ABCD中,E是对角线AC上的一点.连接BE,DE,BE=DE,∠AEB=∠AED,求证:四边形ABCD是菱形.
20.(6分)2023年6月26日是第27个国际禁毒日,某校对学校全体学生进行了毒品预防的教育,为了解学生对毒品预防知识的了解程度,学校开展了“毒品知识知多少”的知识竞赛活动,随机抽取了七年级、八年级学生若干名(抽取的各年级学生人数相同)进行知识答题竞赛,并对得分情况进行整理和分析(得分用整数x表示,单位:分),且分为A,B,C三个等级,分别是:优秀为A等级:85≤x≤100,合格为B等级:70≤x<85,不合格为C等级:0≤x<70.分别绘制成如下统计图表,其中七年级学生测试成绩数据的众数出现在A组,A组测试成绩情况分别为:85,85,87,92,95,95,95,95,97,98,99,100;八年级学生测试成绩数据的A组共有个a人.
七年级、八年级两组样本数据的平均数、中位数、众数和方差如表所示:
成绩 平均数 中位数 众数 方差
七年级 85 b v 99.5
八年级 85 91 96 95.1
根据以上信息,解答下列问题:
(1)填空:a=__________,b=__________,c=__________;
(2)根据以上数据,你认为该学校哪个年级的测试成绩更好,并说明理由:
(3)若该校七、八年级分别有2000人,请估计该校初中七、八年级学生中成绩为优秀的学生共有多少名?
21.(6分)如图.,在平行四边形ABCD中,对角线AC、BD相交于点O,∠ABC=90°
(1)求证:∠BDC=∠ACD;
(2)若点E、F分别为线段AB、AO的中点,连接EF,,,求BC的长及四边形ABCD的面积.
22.(8分)某地允许市场经营主体在规范有序的条件下,采取“店铺外摆”“露天市场”方式进行销售.个体业主小王响应号召,采取“店铺外摆”方式销售甲、乙两种特价商品,两种商品的进价与售价如表所示:
甲商品 乙商品
进价(元/件) 40 10
售价(元/件) 50 15
小王计划购进甲、乙两种商品共100件进行销售,设小王购进甲商品x件,甲、乙两种商品全部销售完后获得的利润为y元.
(1)求出y与x之间的函数关系式;
(2)若购进乙商品的件数不少于甲商品件数的4倍,当购进甲、乙两种商品各多少件时,可使得甲、乙两种商品全部销售完后获得的利润最大?最大利润是多少?
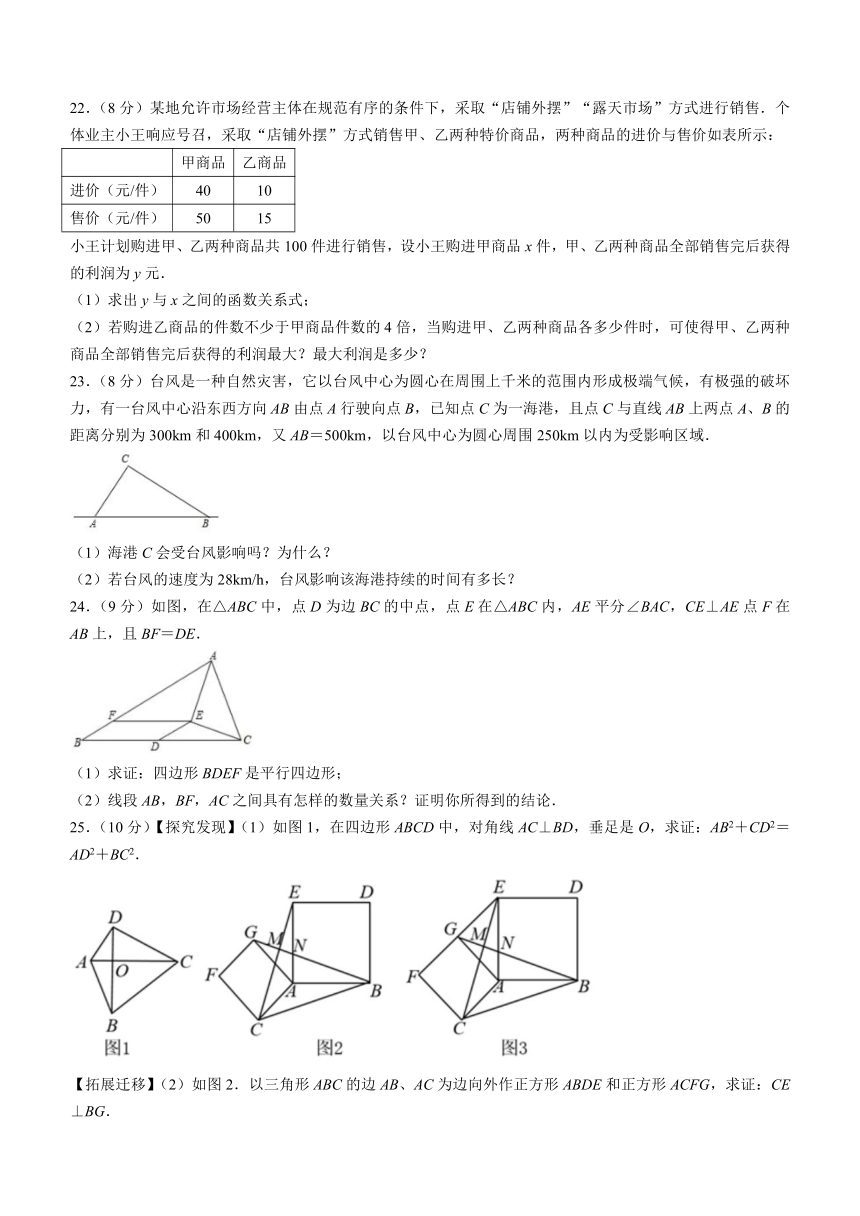
23.(8分)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A、B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C会受台风影响吗?为什么?
(2)若台风的速度为28km/h,台风影响该海港持续的时间有多长?
24.(9分)如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE.
(1)求证:四边形BDEF是平行四边形;
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.
25.(10分)【探究发现】(1)如图1,在四边形ABCD中,对角线AC⊥BD,垂足是O,求证:AB2+CD2=AD2+BC2.
【拓展迁移】(2)如图2.以三角形ABC的边AB、AC为边向外作正方形ABDE和正方形ACFG,求证:CE⊥BG.
(3)如图3,在(2)小题条件不变的情况下,连接GE,若∠EGA=90°,GE=6,AG=8,则BC的长是多少?
2022-2023学年第二学期学业水平监测
八年级数学参考答案
一、选择题(每小题2分,共24分)
序号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C C D B C C B B B A C
二、填空题(每小题3分,共12分)
13.14.>15.20 16.
三、解答题(本大题9小题,共64分)
17.(5分)解:(1)原式
18.解:
=x(x-1)+(x-2)
=x2-x+x-2
=x2-2
当时,原式
19.(本题满分6分)
证明:在△BEC和△DEC中,
∴△ABE≌△ADE(SAS)
∴AB=AD,
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
20.(本题满分6分)
(1)a=13b=86a=95
(2)解:八年级的成绩比较好,理由如下:
两个年级的平均成绩相同,但是八年级的中位数比七年级的大,并且八年级的方差比七年级的方差小,即八年级的成绩更加稳定,
∴八年级的成绩比较好;
(3)解:名,
答:该校初中七、八年级学生中成绩为优秀的学生共有2500名。
21.(本题满分6分)
解:(1)∵,∠ABC=90°,∴四边形ABCD是矩形,
∴AC=BD,OD=OC,∴∠ACD=∠BDC.
(2)∵E,F分别为AB、AO的中点,∴OB=2EF=5,
又∵四边形ABCD是矩形,又BC=6,∠ABC=90°,
∴,∴四边形ABCD的面积为6×8=48.
22.(本题满分8分)
(1)解:由题意可得:y=(50-40)x+(15-10)(100-x),
∴y与x之间的函数关系式为;
(2)由题意,得100-x≥4x,解得x≤20.
∵y=5x+500,∴k=5>0,
∴y随x增大而增大,∴当x=20时,y的值最大,y=5×20+500=600
100-20=70,
答:当购进甲种商品20件,乙种商品70件时,可使得甲、乙商品全部销售完后获得的利润最大为600元.
23.(本题满分8分)
(1)解:如图所示,过点C作CD⊥AB于D点,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,∴△ABC为直角三角形,
∴,∴300×400=500CD,
∴CD=240km,
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C会受到台风影响;
(2)由(1)得CD=240km,
如图所示,当EC=FC=250km时,即台风经过EF段时,正好影响到海港C,此时△ECF为等腰三角形,
,
∴EF=140km,
∵台风的速度为28km/h,
∴140÷28=5h,
∴台风影响该海港持续的时间有5h.
24.(本题满分9分)
(1)证明:延长CE交AB于点G
∵AE⊥CE,∴∠AEG=∠AEC=90°
在△AEG和△AEC,
∴△AEG≌△AEC(ASA),∴GE=EC
∵BD=CD,∴DE为△CGB的中位线
∴DE∥AB,∵DE=BF
∴四边形BDEF是平行四边形.
(2)
理由如下:
∵四边形BDEF是平行四边形,∴BF=DE
∵D,E分别是BC,GC的中点,∴
∵△AEG≌△AEC,∴AG=AC,.
25.(本题满分10分)
证明:
(1)∵AC⊥BD,∴∠AOD=∠AOB=∠COD=∠BOC=90°,由勾股定理得:
AB2+CD2=OA2+OB2+OD2+OC2,
AD2+BC2=OA2+OD2+OB2+OC2,
∴AB2+CD2=AD2+BC2;
(2)∵在正方形ABDE和正方形ACFG中,AC=AG,AE=AB,∠CAG=∠EAB=90°,
∴∠CAG+∠GAE=∠EAB+∠GAE,即∠CAE=∠GAB,
∴△CAE≌△GAB(SAS),
∴∠CEA=∠GBA,
∵∠GBA+∠ANB=90°,∠ANB=∠MNE,
∴∠CEA+∠MNE=90°,∴∠EMN=90°,
(3)如图,连接CG,BE,
∵∠EGA=90°,GE=6,AG=8,∴,
∴AB=10,∴,
∵CE⊥BG,
∴由(1)可知:GE2+BC2=CG2+BE2,即:36+BC2=128+200.
∵BC>0,∴.
八年级数学
注意事项:
1.共三个大题,满分100分,时间120分钟;
2.请用黑墨水的钢笔或水性笔在答题卡上作答,选择题在答题卡上用2B铅笔作答。
一、选择题(本大题共12小题,每小题2分,共24分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)
1.下列实数中,比大的数是()
A.1 B. C.2 D.
2.如图,在中,∠A=125°,则∠1=()
A.65° B.50° C.55° D.45°
3.下列长度的线段不能构成直角三角形的是()
A.3,4,5 B.5,12,13 C.1,2,3 D.6,8,10
4.若式子在实数范围内有意义,则x的取值范围是()
A.x≥2 B.x>2 C.x<2 D.x≤2
5.菱形两条对角线长为12cm和16cm,则菱形周长为()cm.
A.24 B.40 C.32 D.42
6.下列计算正确的是()
A. B.
C. D.
7.对于函数y=12x-4,下列结论正确的是()
A.y的值随x值的增大而减小 B.它的图象经过第一、二、三象限
C.当时,y>0 D.它的图象必经过点(-4,0)
8.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3和S4.若S1=2,S2=8,S4=3,则S3的值是()
A.8 B.7 C.6 D.5
9.我校英语兴趣小组20名学生某日记单词数量如下表所示:
单词数量/个 6 810 12 14
人数/人 3 2 5 6 2
这些学生某日记单词数量的中位数、众数分别是()
A.8,10 B.10,12 C.5,6 D.8,12
10.如图,长方形ABCD的顶点A,B在数轴上,点A表示-1,AB=3,AD=1.若以点A为圆心,对角线AC长为半径作弧,交数轴正半轴于点M,则点M所表示的数为()
A. B. C. D.
11.如图,在长方形ABCD中,点E是CD上一点,连接AE,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.若AB=9,CE=4,则折痕AE的长度为()
A. B. C. D.
12.某学校准备购买一批作业本,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费,甲、乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图分别如图中甲、乙所示,下列三种说法:
①甲厂的制版费为1千元;
②当印制作业本超过2千个时,乙厂的印刷费用为0.2元/个;
③当印制作业本8千个时,应选择乙厂,可节省费用500元。
其中正确的说法有()
A.①② B.②③ C.①③ D.①②③
二、填空题(本大题共4小题,每小题3分,共12分)
13.计算的结果是__________.
14.在一次“一分钟跳绳”比赛中,甲、乙两人各跳三轮,两人三次跳绳个数的平均数均是182个,他们成绩的方差分别记为,,若甲、乙两人在这三轮比赛中乙成绩更稳定,那么,的大小关系是_________(填“>”,“<”,“=”)
15.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为__________.
16.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是__________.
三、解答题(本大题共9小题,共64分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(5分)计算
18.(6分)先化简,再求值:,其中
19.(6分)如图,在平行四边形ABCD中,E是对角线AC上的一点.连接BE,DE,BE=DE,∠AEB=∠AED,求证:四边形ABCD是菱形.
20.(6分)2023年6月26日是第27个国际禁毒日,某校对学校全体学生进行了毒品预防的教育,为了解学生对毒品预防知识的了解程度,学校开展了“毒品知识知多少”的知识竞赛活动,随机抽取了七年级、八年级学生若干名(抽取的各年级学生人数相同)进行知识答题竞赛,并对得分情况进行整理和分析(得分用整数x表示,单位:分),且分为A,B,C三个等级,分别是:优秀为A等级:85≤x≤100,合格为B等级:70≤x<85,不合格为C等级:0≤x<70.分别绘制成如下统计图表,其中七年级学生测试成绩数据的众数出现在A组,A组测试成绩情况分别为:85,85,87,92,95,95,95,95,97,98,99,100;八年级学生测试成绩数据的A组共有个a人.
七年级、八年级两组样本数据的平均数、中位数、众数和方差如表所示:
成绩 平均数 中位数 众数 方差
七年级 85 b v 99.5
八年级 85 91 96 95.1
根据以上信息,解答下列问题:
(1)填空:a=__________,b=__________,c=__________;
(2)根据以上数据,你认为该学校哪个年级的测试成绩更好,并说明理由:
(3)若该校七、八年级分别有2000人,请估计该校初中七、八年级学生中成绩为优秀的学生共有多少名?
21.(6分)如图.,在平行四边形ABCD中,对角线AC、BD相交于点O,∠ABC=90°
(1)求证:∠BDC=∠ACD;
(2)若点E、F分别为线段AB、AO的中点,连接EF,,,求BC的长及四边形ABCD的面积.
22.(8分)某地允许市场经营主体在规范有序的条件下,采取“店铺外摆”“露天市场”方式进行销售.个体业主小王响应号召,采取“店铺外摆”方式销售甲、乙两种特价商品,两种商品的进价与售价如表所示:
甲商品 乙商品
进价(元/件) 40 10
售价(元/件) 50 15
小王计划购进甲、乙两种商品共100件进行销售,设小王购进甲商品x件,甲、乙两种商品全部销售完后获得的利润为y元.
(1)求出y与x之间的函数关系式;
(2)若购进乙商品的件数不少于甲商品件数的4倍,当购进甲、乙两种商品各多少件时,可使得甲、乙两种商品全部销售完后获得的利润最大?最大利润是多少?
23.(8分)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A、B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C会受台风影响吗?为什么?
(2)若台风的速度为28km/h,台风影响该海港持续的时间有多长?
24.(9分)如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE.
(1)求证:四边形BDEF是平行四边形;
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.
25.(10分)【探究发现】(1)如图1,在四边形ABCD中,对角线AC⊥BD,垂足是O,求证:AB2+CD2=AD2+BC2.
【拓展迁移】(2)如图2.以三角形ABC的边AB、AC为边向外作正方形ABDE和正方形ACFG,求证:CE⊥BG.
(3)如图3,在(2)小题条件不变的情况下,连接GE,若∠EGA=90°,GE=6,AG=8,则BC的长是多少?
2022-2023学年第二学期学业水平监测
八年级数学参考答案
一、选择题(每小题2分,共24分)
序号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C C D B C C B B B A C
二、填空题(每小题3分,共12分)
13.14.>15.20 16.
三、解答题(本大题9小题,共64分)
17.(5分)解:(1)原式
18.解:
=x(x-1)+(x-2)
=x2-x+x-2
=x2-2
当时,原式
19.(本题满分6分)
证明:在△BEC和△DEC中,
∴△ABE≌△ADE(SAS)
∴AB=AD,
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
20.(本题满分6分)
(1)a=13b=86a=95
(2)解:八年级的成绩比较好,理由如下:
两个年级的平均成绩相同,但是八年级的中位数比七年级的大,并且八年级的方差比七年级的方差小,即八年级的成绩更加稳定,
∴八年级的成绩比较好;
(3)解:名,
答:该校初中七、八年级学生中成绩为优秀的学生共有2500名。
21.(本题满分6分)
解:(1)∵,∠ABC=90°,∴四边形ABCD是矩形,
∴AC=BD,OD=OC,∴∠ACD=∠BDC.
(2)∵E,F分别为AB、AO的中点,∴OB=2EF=5,
又∵四边形ABCD是矩形,又BC=6,∠ABC=90°,
∴,∴四边形ABCD的面积为6×8=48.
22.(本题满分8分)
(1)解:由题意可得:y=(50-40)x+(15-10)(100-x),
∴y与x之间的函数关系式为;
(2)由题意,得100-x≥4x,解得x≤20.
∵y=5x+500,∴k=5>0,
∴y随x增大而增大,∴当x=20时,y的值最大,y=5×20+500=600
100-20=70,
答:当购进甲种商品20件,乙种商品70件时,可使得甲、乙商品全部销售完后获得的利润最大为600元.
23.(本题满分8分)
(1)解:如图所示,过点C作CD⊥AB于D点,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,∴△ABC为直角三角形,
∴,∴300×400=500CD,
∴CD=240km,
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C会受到台风影响;
(2)由(1)得CD=240km,
如图所示,当EC=FC=250km时,即台风经过EF段时,正好影响到海港C,此时△ECF为等腰三角形,
,
∴EF=140km,
∵台风的速度为28km/h,
∴140÷28=5h,
∴台风影响该海港持续的时间有5h.
24.(本题满分9分)
(1)证明:延长CE交AB于点G
∵AE⊥CE,∴∠AEG=∠AEC=90°
在△AEG和△AEC,
∴△AEG≌△AEC(ASA),∴GE=EC
∵BD=CD,∴DE为△CGB的中位线
∴DE∥AB,∵DE=BF
∴四边形BDEF是平行四边形.
(2)
理由如下:
∵四边形BDEF是平行四边形,∴BF=DE
∵D,E分别是BC,GC的中点,∴
∵△AEG≌△AEC,∴AG=AC,.
25.(本题满分10分)
证明:
(1)∵AC⊥BD,∴∠AOD=∠AOB=∠COD=∠BOC=90°,由勾股定理得:
AB2+CD2=OA2+OB2+OD2+OC2,
AD2+BC2=OA2+OD2+OB2+OC2,
∴AB2+CD2=AD2+BC2;
(2)∵在正方形ABDE和正方形ACFG中,AC=AG,AE=AB,∠CAG=∠EAB=90°,
∴∠CAG+∠GAE=∠EAB+∠GAE,即∠CAE=∠GAB,
∴△CAE≌△GAB(SAS),
∴∠CEA=∠GBA,
∵∠GBA+∠ANB=90°,∠ANB=∠MNE,
∴∠CEA+∠MNE=90°,∴∠EMN=90°,
(3)如图,连接CG,BE,
∵∠EGA=90°,GE=6,AG=8,∴,
∴AB=10,∴,
∵CE⊥BG,
∴由(1)可知:GE2+BC2=CG2+BE2,即:36+BC2=128+200.
∵BC>0,∴.
同课章节目录
