27.2.1 相似三角形的判定(1)
文档属性
| 名称 | 27.2.1 相似三角形的判定(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 640.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-14 00:00:00 | ||
图片预览

文档简介
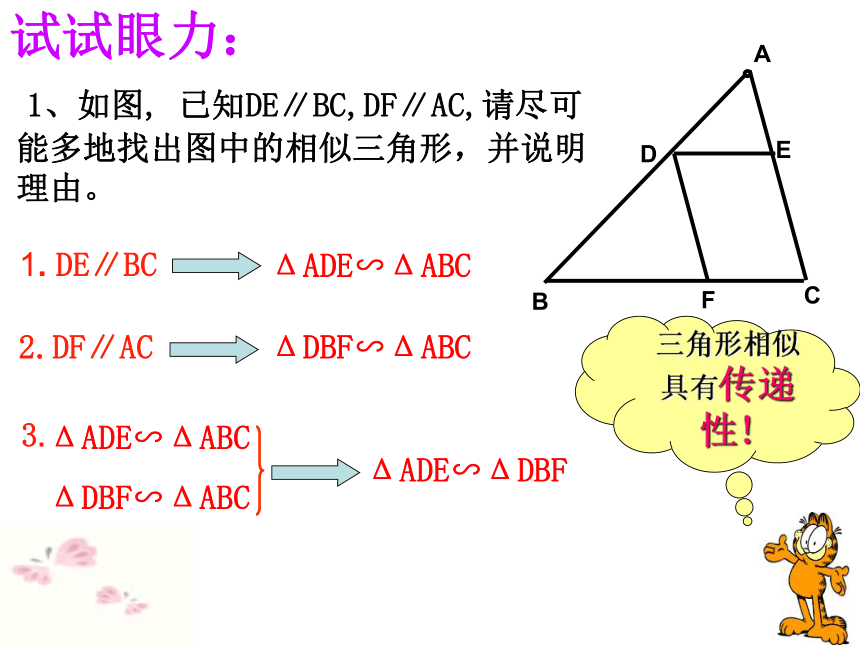
课件23张PPT。27.2.1 相似三角形的判定(一)相似多边形的判定:观察回顾:对应角相等,对应边的比相等
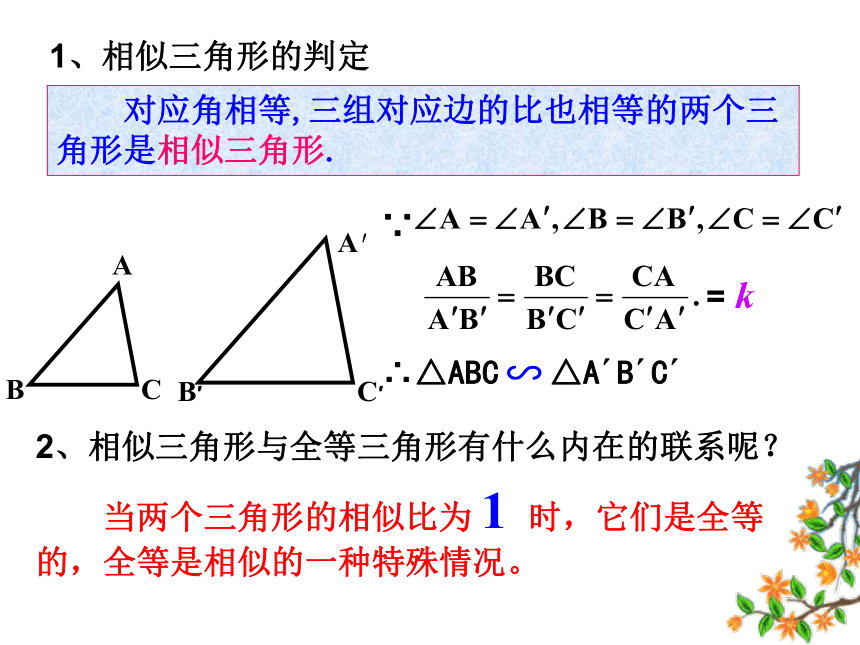
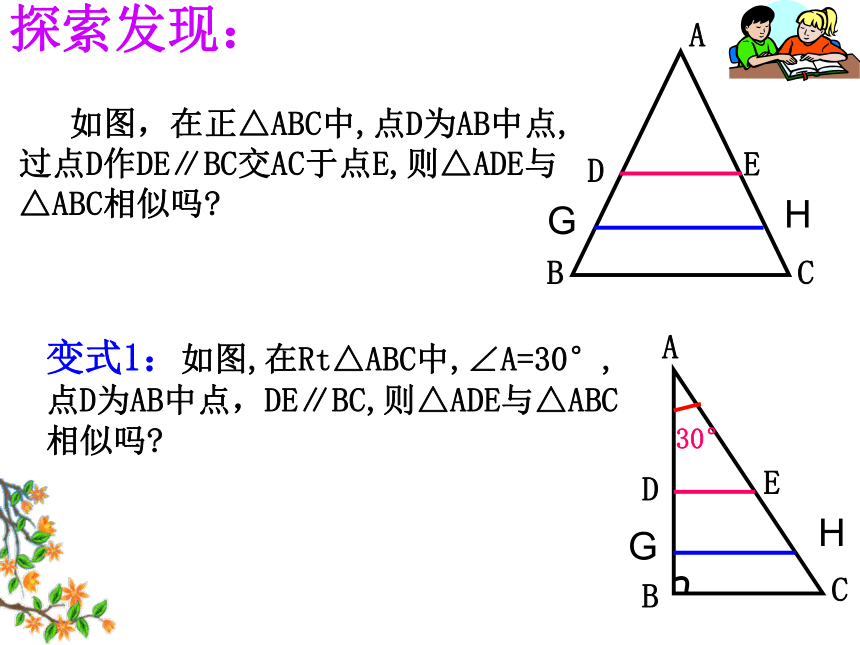
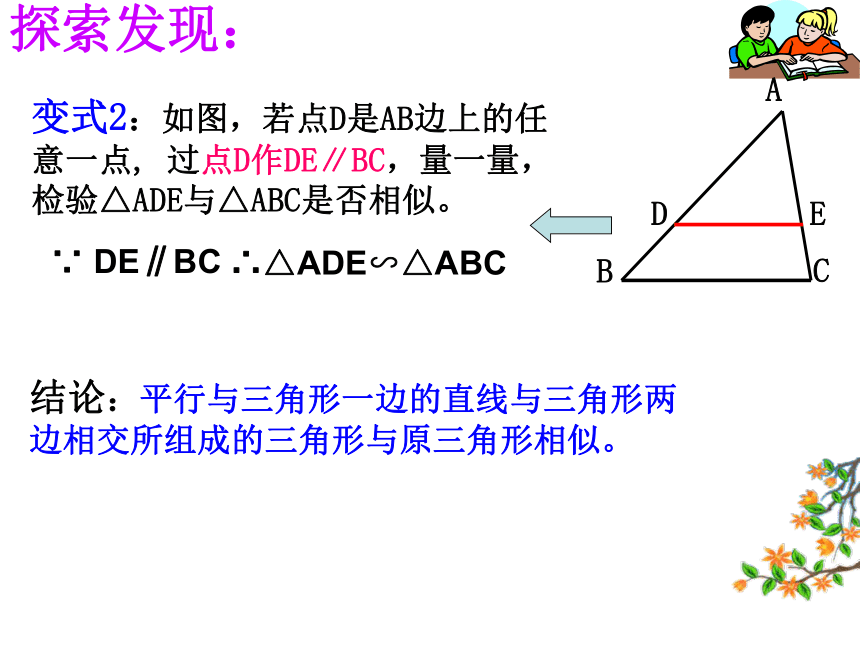
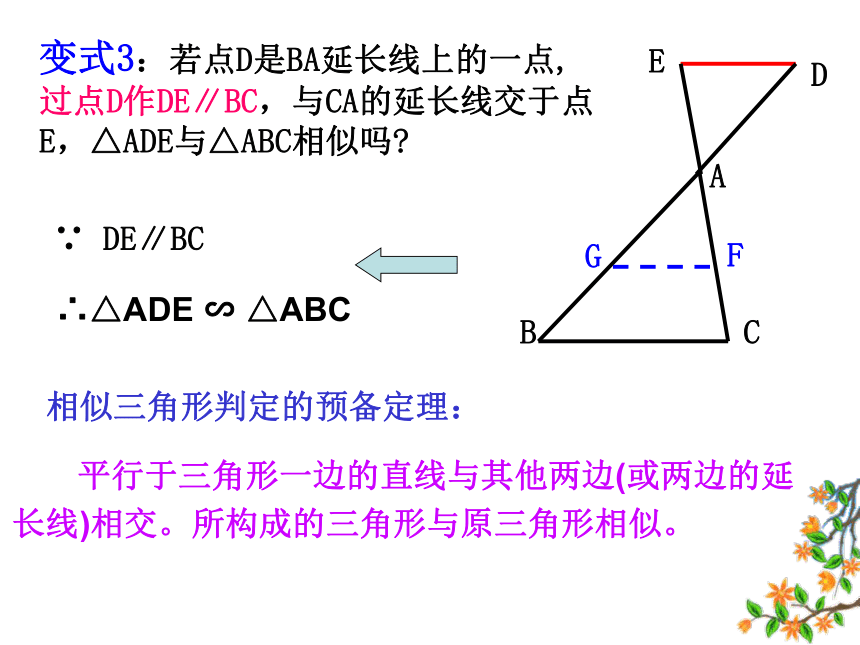
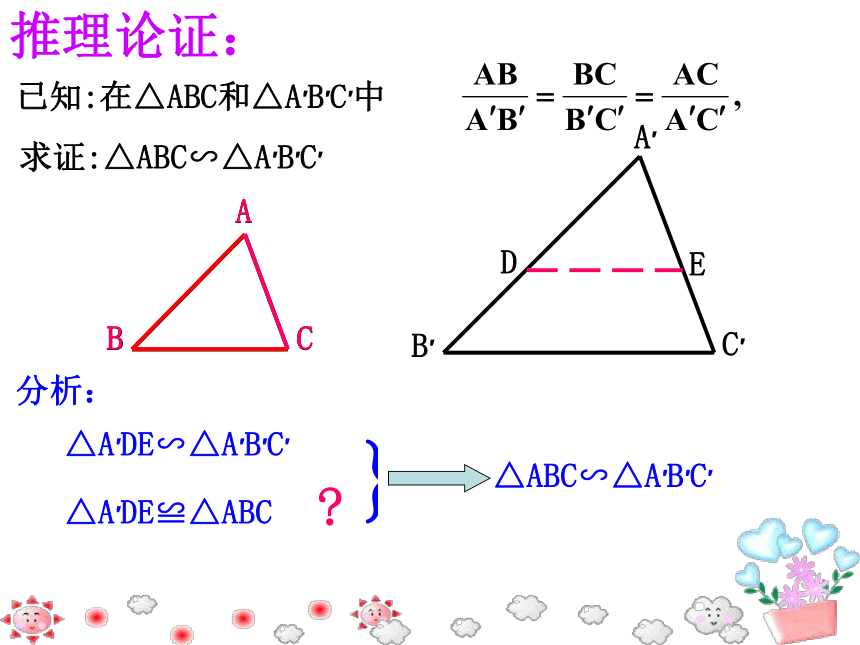
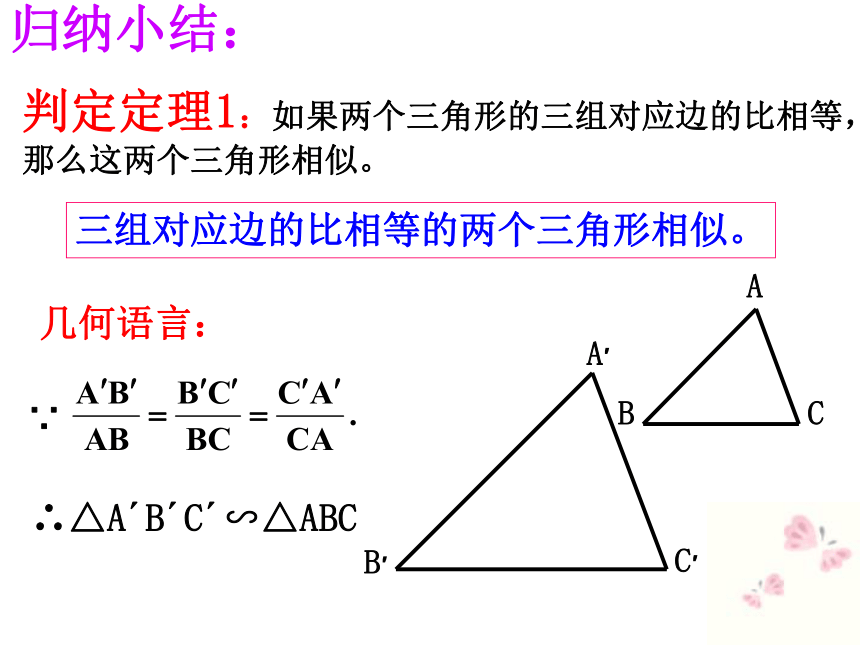
的两个多边形为相似多边形。 当两个三角形的相似比为 1 时,它们是全等的,全等是相似的一种特殊情况。 对应角相等,三组对应边的比也相等的两个三角形是相似三角形.1、相似三角形的判定2、相似三角形与全等三角形有什么内在的联系呢?= k∴△ABC △A′B′C′∽ 如图,在正△ABC中,点D为AB中点,过点D作DE∥BC交AC于点E,则△ADE与△ABC相似吗?探索发现:变式1:如图,在Rt△ABC中,∠A=30°, 点D为AB中点,DE∥BC,则△ADE与△ABC相似吗?GHGH变式2:如图,若点D是AB边上的任意一点, 过点D作DE∥BC,量一量,检验△ADE与△ABC是否相似。∵ DE∥BC∴△ADE∽△ABC探索发现:结论:平行与三角形一边的直线与三角形两边相交所组成的三角形与原三角形相似。试试眼力:三角形相似具有传递性!1. DE∥BC2.DF∥ACΔADE∽ΔDBFΔDBF∽ΔABCΔADE∽ΔABC变式3:若点D是BA延长线上的一点,过点D作DE∥BC,与CA的延长线交于点E,△ADE与△ABC相似吗?∵ DE∥BC∴△ADE ∽ △ABC 平行于三角形一边的直线与其他两边(或两边的延长线)相交。所构成的三角形与原三角形相似。相似三角形判定的预备定理:推理论证:分析:?归纳小结:判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:三组对应边的比相等的两个三角形相似。∴△A′B′C′∽△ABC牛刀小试: 根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12△ABC∽△DEF△ABC∽不 相 似△EDFDE=6,EF=12,DF=8△ABC∽△DEF例题教学:例2 如图,判断4×4方格中的两个三角形是否相似,并说明理由.例题教学:例1 求证:三角形的三条中位线所组成的三角形 与原三角形相似。已知:求证:如图,DE,DF,EF是△ABC的中位线△ABC∽△FED证明:∵ DE,DF,EF是△ABC的中位线∴ DE= BC,DF= AC,EF= AB∴ △ABC∽△DEF例题教学:已知:如图,DE,DF,EF是△ABC的中位线。(1)请找出图中的相似三角形。1、如图,在 ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE、BD交于点F,则BE:AD=_____,BF:FD_____。2、如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=______。反馈练习:3:53:53:5变式3:若 BF=3,CF=2,AD=1.5,DF=6,你能求出线段AE的长度吗?巩固提高:2∴△BDF∽△BAC∵DF∥AC解:∵DE∥BC,DF∥AC∴四边形DFCE为平行四边形∴FC=DE=2,EC=DF=66∴AE=AC-CE=10-6=4如图:一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗? 若用皮尺测得:BC=40米,CD=20米,DE=60米,你能计算出电线杆A与大树B之间的距离吗?ABCDE学以致用请你帮忙: 图纸上上有不锈钢三角架的长分别为3cm,4cm,5cm,库存的不锈钢条有两根中,一根长60cm,另一根长180cm,工人师傅想用其中一根做三角架的一边,在另一根上取两截,用来做三角架的另外两边,使做成的三角架与图纸上的形状相同(即图形相似)。请帮他确定:共有几种不同的做法(焊接用料略去不计)?哪一种放大的倍数最大?最大的倍数是多少?相似三角形判定方法1、三组对应边的比相等且对应角相等;3、三组对应边的比相等的两个三角形相似。2、平行于三角形一边的直线与其他两边(或 两边的延长线)相交,所构成的三角形与原三角形相似。总结反思 与同桌交流一下你这节课的收获! 作业:选做题:《作业本》必做题:《课本》P55 面
第1、3、4、5题www.czsx.com.cn再见 !例题教学:证明:即 ∠BAD=∠CAE∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC ∴△BDM∽△BAC解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB3份巩固练习:合作学习: 为美化校园,学校决定对东教学楼后面的一块三角形的空地(如图)进行修整,现已测量出AB=12m,BC=16m,CA=24m,请你用适当的比例为这块空地画出图纸。1.量一量,与同桌交流一下,你们所画的两个三角形的对应角相等吗?2.猜测:三组对应边的比相等的两个三角形是否相似?
的两个多边形为相似多边形。 当两个三角形的相似比为 1 时,它们是全等的,全等是相似的一种特殊情况。 对应角相等,三组对应边的比也相等的两个三角形是相似三角形.1、相似三角形的判定2、相似三角形与全等三角形有什么内在的联系呢?= k∴△ABC △A′B′C′∽ 如图,在正△ABC中,点D为AB中点,过点D作DE∥BC交AC于点E,则△ADE与△ABC相似吗?探索发现:变式1:如图,在Rt△ABC中,∠A=30°, 点D为AB中点,DE∥BC,则△ADE与△ABC相似吗?GHGH变式2:如图,若点D是AB边上的任意一点, 过点D作DE∥BC,量一量,检验△ADE与△ABC是否相似。∵ DE∥BC∴△ADE∽△ABC探索发现:结论:平行与三角形一边的直线与三角形两边相交所组成的三角形与原三角形相似。试试眼力:三角形相似具有传递性!1. DE∥BC2.DF∥ACΔADE∽ΔDBFΔDBF∽ΔABCΔADE∽ΔABC变式3:若点D是BA延长线上的一点,过点D作DE∥BC,与CA的延长线交于点E,△ADE与△ABC相似吗?∵ DE∥BC∴△ADE ∽ △ABC 平行于三角形一边的直线与其他两边(或两边的延长线)相交。所构成的三角形与原三角形相似。相似三角形判定的预备定理:推理论证:分析:?归纳小结:判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:三组对应边的比相等的两个三角形相似。∴△A′B′C′∽△ABC牛刀小试: 根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12△ABC∽△DEF△ABC∽不 相 似△EDFDE=6,EF=12,DF=8△ABC∽△DEF例题教学:例2 如图,判断4×4方格中的两个三角形是否相似,并说明理由.例题教学:例1 求证:三角形的三条中位线所组成的三角形 与原三角形相似。已知:求证:如图,DE,DF,EF是△ABC的中位线△ABC∽△FED证明:∵ DE,DF,EF是△ABC的中位线∴ DE= BC,DF= AC,EF= AB∴ △ABC∽△DEF例题教学:已知:如图,DE,DF,EF是△ABC的中位线。(1)请找出图中的相似三角形。1、如图,在 ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE、BD交于点F,则BE:AD=_____,BF:FD_____。2、如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=______。反馈练习:3:53:53:5变式3:若 BF=3,CF=2,AD=1.5,DF=6,你能求出线段AE的长度吗?巩固提高:2∴△BDF∽△BAC∵DF∥AC解:∵DE∥BC,DF∥AC∴四边形DFCE为平行四边形∴FC=DE=2,EC=DF=66∴AE=AC-CE=10-6=4如图:一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗? 若用皮尺测得:BC=40米,CD=20米,DE=60米,你能计算出电线杆A与大树B之间的距离吗?ABCDE学以致用请你帮忙: 图纸上上有不锈钢三角架的长分别为3cm,4cm,5cm,库存的不锈钢条有两根中,一根长60cm,另一根长180cm,工人师傅想用其中一根做三角架的一边,在另一根上取两截,用来做三角架的另外两边,使做成的三角架与图纸上的形状相同(即图形相似)。请帮他确定:共有几种不同的做法(焊接用料略去不计)?哪一种放大的倍数最大?最大的倍数是多少?相似三角形判定方法1、三组对应边的比相等且对应角相等;3、三组对应边的比相等的两个三角形相似。2、平行于三角形一边的直线与其他两边(或 两边的延长线)相交,所构成的三角形与原三角形相似。总结反思 与同桌交流一下你这节课的收获! 作业:选做题:《作业本》必做题:《课本》P55 面
第1、3、4、5题www.czsx.com.cn再见 !例题教学:证明:即 ∠BAD=∠CAE∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC ∴△BDM∽△BAC解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB3份巩固练习:合作学习: 为美化校园,学校决定对东教学楼后面的一块三角形的空地(如图)进行修整,现已测量出AB=12m,BC=16m,CA=24m,请你用适当的比例为这块空地画出图纸。1.量一量,与同桌交流一下,你们所画的两个三角形的对应角相等吗?2.猜测:三组对应边的比相等的两个三角形是否相似?
