28.2 解直角三角形(1)
文档属性
| 名称 | 28.2 解直角三角形(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 371.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-14 00:00:00 | ||
图片预览






文档简介
课件18张PPT。28.2 解直角三角形(1)ABCBC=5.2mAB=54.5mα高54.5m的斜塔偏离垂直中心线的距离为5.2m,求塔身偏离中心线的角度。要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:问题情景(1)使用这个梯子最高可以安全攀上多高的平房?(精确到0.1m)这个问题归结为:
在Rt△ABC中,已知∠A= 75°,斜边AB=6,求BC的长角α越大,攀上的高度就越高.ACB要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:问题情景(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能否安全使用这个梯子?这个问题归结为:
在Rt△ABC中,已知AC=2.4m,斜边AB=6, 求锐角α的度数?ACB要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:问题情景(3)梯子底端最远可以距离墙面多远?(精确到0.1m)这个问题归结为:
在Rt△ABC中,已知∠A= 50°,斜边AB=6,求AC的长角α越小,梯子底端距离墙面越远.ACB探究:在Rt△ABC中,(1)根据∠A= 75°,斜边AB=6,
你能求出这个三角形的其他元素吗?(2)根据AC=2.4m,斜边AB=6,
你能求出这个三角形的其他元素吗?三角形有六个元素,分别是三条边和三个角.在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.(3)根据∠A=60°,∠B=30°,
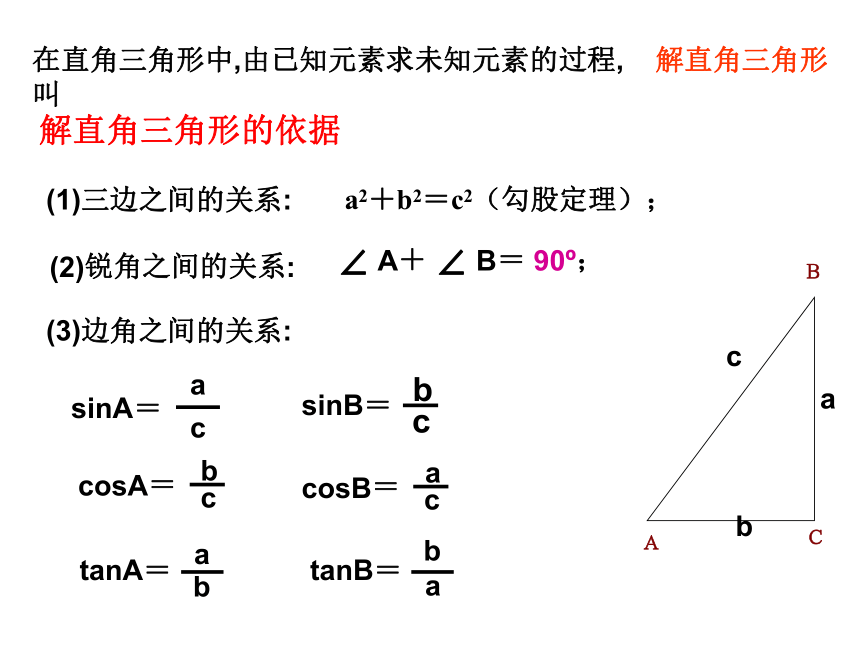
你能求出这个三角形的其他元素吗?ACB(其中至少有一个是边),在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);解直角三角形的依据(2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=sinB=??? 例1 :在△ABC中,∠C=90°, ,
,解这个直角三角形 . ABCabc?????例2 在Rt△ABC中,∠C=90°, ∠B=35°, b=20 , 解这个直角三角形 (精确到0.1).ABCabc2035°???巩固练习1.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形
a=30 ,b=20
∠B=72°, c=14 台风是一种空气旋涡,是破坏力很强的自然灾害。2006年5月18日2时15分,台风“珍珠”在广东汕头澄海和饶平之间登陆,一棵百年大树被吹断折倒在地上,你知道这棵大树在折断之前有多高吗? 直接测量被折断的两部分树干AC和AB的长度,再把它们加起来.大树高度=AB+ACABC 测量地面距离BC和被折断的树干AC或AB的长度,再用勾股定理解答. 先用测角仪测量∠B的度数,再测量地面距离BC的长度,用锐角三角函数知识解答.情景分析如何知道这棵大树在折断之前有多高?方案一:方案二:方案三:CCAABB⌒⌒⌒⌒⌒⌒⌒例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。尝试一下: 你还有其它方法吗?请同学们试着用这两种方法做做看。 (小组合作)例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。 在△ABC中,∠B=600,AD⊥BC,AD= ,AC= ,则AB= ,BC= ;如图,在△ABC,∠C=90O,D是BC的中点,∠ADC=60O,AC= ,求:△ABD的周长梯形ABCD中,AD∥BC,∠B=45O,∠C=120O,AB=8,求CD的长例3: 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.AB的长D
在Rt△ABC中,已知∠A= 75°,斜边AB=6,求BC的长角α越大,攀上的高度就越高.ACB要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:问题情景(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能否安全使用这个梯子?这个问题归结为:
在Rt△ABC中,已知AC=2.4m,斜边AB=6, 求锐角α的度数?ACB要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子.问:问题情景(3)梯子底端最远可以距离墙面多远?(精确到0.1m)这个问题归结为:
在Rt△ABC中,已知∠A= 50°,斜边AB=6,求AC的长角α越小,梯子底端距离墙面越远.ACB探究:在Rt△ABC中,(1)根据∠A= 75°,斜边AB=6,
你能求出这个三角形的其他元素吗?(2)根据AC=2.4m,斜边AB=6,
你能求出这个三角形的其他元素吗?三角形有六个元素,分别是三条边和三个角.在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元素吗?ACB(其中至少有一个是边),在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);解直角三角形的依据(2)锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=sinB=??? 例1 :在△ABC中,∠C=90°, ,
,解这个直角三角形 . ABCabc?????例2 在Rt△ABC中,∠C=90°, ∠B=35°, b=20 , 解这个直角三角形 (精确到0.1).ABCabc2035°???巩固练习1.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形
a=30 ,b=20
∠B=72°, c=14 台风是一种空气旋涡,是破坏力很强的自然灾害。2006年5月18日2时15分,台风“珍珠”在广东汕头澄海和饶平之间登陆,一棵百年大树被吹断折倒在地上,你知道这棵大树在折断之前有多高吗? 直接测量被折断的两部分树干AC和AB的长度,再把它们加起来.大树高度=AB+ACABC 测量地面距离BC和被折断的树干AC或AB的长度,再用勾股定理解答. 先用测角仪测量∠B的度数,再测量地面距离BC的长度,用锐角三角函数知识解答.情景分析如何知道这棵大树在折断之前有多高?方案一:方案二:方案三:CCAABB⌒⌒⌒⌒⌒⌒⌒例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。尝试一下: 你还有其它方法吗?请同学们试着用这两种方法做做看。 (小组合作)例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。 在△ABC中,∠B=600,AD⊥BC,AD= ,AC= ,则AB= ,BC= ;如图,在△ABC,∠C=90O,D是BC的中点,∠ADC=60O,AC= ,求:△ABD的周长梯形ABCD中,AD∥BC,∠B=45O,∠C=120O,AB=8,求CD的长例3: 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.AB的长D
