9.1.2分层随机抽样 课件(共20张ppt)
文档属性
| 名称 | 9.1.2分层随机抽样 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 560.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 21:17:15 | ||
图片预览







文档简介
(共20张PPT)
9.1.2 分层随机抽样
高一数学—人教版—必修二—第九章
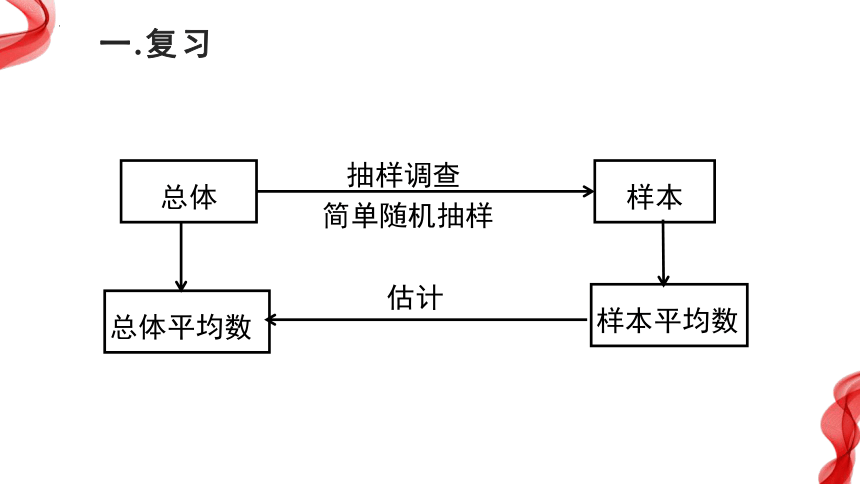
总体
样本
简单随机抽样
样本平均数
估计
总体平均数
抽样调查
一.复习
156.0 157.0 161.0 159.0 156.0 174.0 168.0 155.0 158.0 167.0
166.0 160.0 166.0 175.0 154.0 157.0 173.0 161.0 160.0 171.0
157.0 170.0 174.0 171.5 175.0 153.0 155.0 158.0 167.0 178.0
155.0 175.0 170.0 150.5 155.0 163.0 171.0 160.0 152.0 159.0
162.0 158.0 155.0 153.0 153.0 177.0 166.0 170.0 169.0 150.0
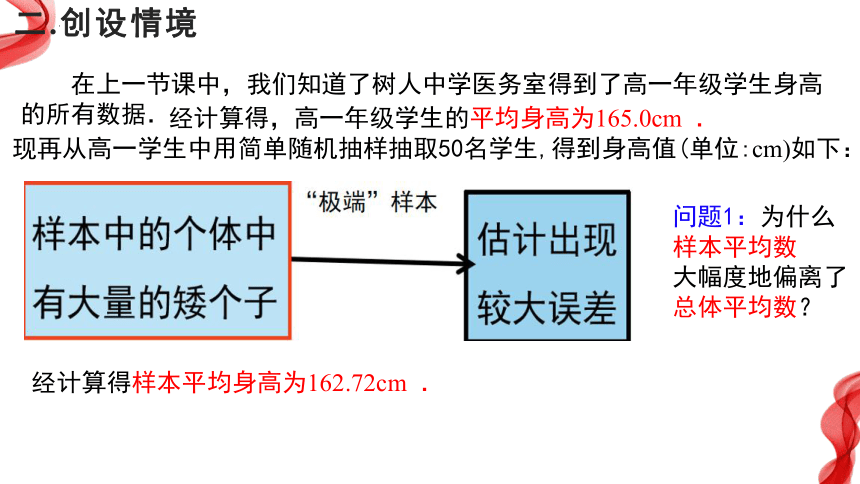
现再从高一学生中用简单随机抽样抽取50名学生,得到身高值(单位:cm)如下:
在上一节课中,我们知道了树人中学医务室得到了高一年级学生身高的所有数据.
经计算得,高一年级学生的平均身高为165.0cm .
二.创设情境
问题1:为什么样本平均数
大幅度地偏离了总体平均数?
经计算得样本平均身高为162.72cm .
问题2:为什么运用简单随机抽样获取的样本中,会出现“极端”样本?
简单随机抽样存在不足,有必要探究其它的抽样方式.
问题3:如何减少“极端”样本的出现?
把高一学生分成男生和女生两个身高有明显差异的群体.
二.创设情境
若在树人中学高一年级有712名学生,男生有326名、女生有386名.
抽取一个样本量为50的样本.
问题4:对男生、女生分别进行简单随机抽样,样本量在男生、女生中应如何分配?
应按男生、女生在全体学生中所占的比例分配..
按男生、女生在全体学生中所占的比例分配
三.探究新知
当总样本量为50时,可以计算出从男生、女生中分别应抽取的人数为:
这样,无论男生、女生,每个学生被抽到的概率都相等.
(1)定义: 一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样(stratified random sampling),每一个子总体称为层.
四.学习新知
在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配,此比例为抽样比.
在分层随机抽样中,按各层在总体中所占的比例分配样本量,即
1.分层随机抽样
适用范围:当总体是由差异明显的几个部分组成时,往往采用分层随机抽样
练习1. 某社区有700户家庭,其中高收入家庭225户,中等收入家庭400户,低收入家庭75户,为了调查社会购买力的某项指标,要从中抽取一个容量为100户的样本,记作①;
某中学高二年级有12名足球运动员,要从中选出3人调查学习负担情况,记作②,
则完成上述2项应采用的抽样方法是____________.
分层随机抽样
简单随机抽样
依据:个体之间是否有明显的差异
练习2:下列问题中,最适合用分层随机抽样抽取样本的是( )
A.从10名同学中抽取3人参加座谈会
B.某政府机关在编人员共100人,其中副处级以上干部10人,一般干部70人,工人20人,上级部门为了了解该机关对政府机构改革的意见,要从中抽取20人,
C.从1 000名工人中,抽取100人调查上班途中所用时间,
D.从生产流水线上,抽取样本检查产品质量
B
依据:个体之间是否有明显的差异
类别 共同点 各自特点 相互联系 适用范围
简单随机抽样 抽样过程中各个个体被抽到的机会相等 从总体中逐个抽取 最基本的抽样方法 总体容量较少
分层抽样 抽样过程中各个个体被抽到的机会相等 将总体分成几部分,每一部分按比例抽取 每层抽样时采用简单随机抽样 总体由差异明显的若干部分组成
总结:简单随机抽样与分层随机抽样的区别
解:(1)因为不同岗位对改革意见有明显的差异,符合分层随机抽样的特点,故选用分层随机抽样方法.
例1.一个单位有职工160人,其中有业务人员112人,管理人员16人,后勤人员32人,为了了解职工对单位改革意见的某种情况,要从中抽取一个容量为20 的样本,
(1)试确定用何种方法抽取 (2)写出抽样过程
解:
第四步:在各层中分别用简单随机抽样抽取业务人员14人;管理人员2人;
后勤人员4人
例1.一个单位有职工160人,其中有业务人员112人,管理人员16人,后勤人员32人,为了了解职工对单位改革意见的某种情况,要从中抽取一个容量为20 的样本,
(1)试确定用何种方法抽取 (2)写出抽样过程
第一步:按业务人员、后勤人员、管理人员分成三层
第二步:计算抽样比:
第三步:确定各层抽取的样本数:
第五步:将所抽取的个体组合在一起构成样本容量为20的样本
分层随机抽样的步骤:
第二步,计算样本容量与总体的个体数比例
第五步,将各层抽取的个体合在一起,就得到所取样本.
第四步,各层用简单随机抽样的方法抽样;
第三步,将总体分层 ,确定第i层应该抽取的个体数目为
求比
定数
抽样
成样
第一步,根据已掌握信息,将总体分成互不相交的层;
分层
归纳:
问题5:我们从树从中学高一年级712名学生中用分层随机抽样抽取了一个容量为50的样本,如何估计高一年级学生的平均身高?
2.总体平均数的估计
即估计树人中学高一年级学生的平均身高在165.2 cm左右.
问题6:一般地,分层随机抽样中,是否可以直接用样本平均数估计总体平均数?
第1层的总体平均数为
第2层的总体平均数为
第1层样本平均数为
第2层样本平均数为
样本平均数为:
2.总体平均数的估计
总体平均数为
2.总体平均数的估计
用比例分配的分层随机抽样方法,从高一年级的学生中抽取了10个样本量为50的样本,计算出样本平均数如下表.
3.探索不同抽样估计总体的效果
序号 1 2 3 4 5 6 7 8 9 10
样本平均数 165.8 165.1 164.3 164.3 166.4 164.6 165.2 164.9 166.1 165.1
问题7:把分层随机抽样的平均数与上一节样本量为50的简单随机抽样的平均数用图形进行表示,通过比较两次的结果,你有什么发现?
探究:从样本均值估计总体均值的角度,分层随机抽样的估计效果是否一定比简单随机抽样的估计效果好呢?
(2)分层随机抽样样本平均数更均匀,简单随机抽样中出现了“极端”的样
本,分层随机抽样中几乎没有出现;
(3)在个体之间差异较大时,只要选取的分层变量合适,分层随机抽样的效果一般会好于简单随机抽样.
(1)与简单随机抽样的结果比较,分层随机抽样并没有明显优于简单随机抽样;
例2.高二年级有男生490人,女生510人,张华按男生、女生进行分层,通过
分层随机抽样的方法,得到男生、女生的平均身高分别为170.2cm和160.8cm.
如果张华在各层中按等比例分配样本,总样本量为100,那么在男生、女生
中分别抽取了多少名?在这种情况下,请估计高二年级全体学生的平均身高.
(教材第185 页第三题)
五.小结
六.作业
人教A版必修第二册:
184页练习1、2、3、4
188页习题9.1第5、7题
9.1.2 分层随机抽样
高一数学—人教版—必修二—第九章
总体
样本
简单随机抽样
样本平均数
估计
总体平均数
抽样调查
一.复习
156.0 157.0 161.0 159.0 156.0 174.0 168.0 155.0 158.0 167.0
166.0 160.0 166.0 175.0 154.0 157.0 173.0 161.0 160.0 171.0
157.0 170.0 174.0 171.5 175.0 153.0 155.0 158.0 167.0 178.0
155.0 175.0 170.0 150.5 155.0 163.0 171.0 160.0 152.0 159.0
162.0 158.0 155.0 153.0 153.0 177.0 166.0 170.0 169.0 150.0
现再从高一学生中用简单随机抽样抽取50名学生,得到身高值(单位:cm)如下:
在上一节课中,我们知道了树人中学医务室得到了高一年级学生身高的所有数据.
经计算得,高一年级学生的平均身高为165.0cm .
二.创设情境
问题1:为什么样本平均数
大幅度地偏离了总体平均数?
经计算得样本平均身高为162.72cm .
问题2:为什么运用简单随机抽样获取的样本中,会出现“极端”样本?
简单随机抽样存在不足,有必要探究其它的抽样方式.
问题3:如何减少“极端”样本的出现?
把高一学生分成男生和女生两个身高有明显差异的群体.
二.创设情境
若在树人中学高一年级有712名学生,男生有326名、女生有386名.
抽取一个样本量为50的样本.
问题4:对男生、女生分别进行简单随机抽样,样本量在男生、女生中应如何分配?
应按男生、女生在全体学生中所占的比例分配..
按男生、女生在全体学生中所占的比例分配
三.探究新知
当总样本量为50时,可以计算出从男生、女生中分别应抽取的人数为:
这样,无论男生、女生,每个学生被抽到的概率都相等.
(1)定义: 一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样(stratified random sampling),每一个子总体称为层.
四.学习新知
在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配,此比例为抽样比.
在分层随机抽样中,按各层在总体中所占的比例分配样本量,即
1.分层随机抽样
适用范围:当总体是由差异明显的几个部分组成时,往往采用分层随机抽样
练习1. 某社区有700户家庭,其中高收入家庭225户,中等收入家庭400户,低收入家庭75户,为了调查社会购买力的某项指标,要从中抽取一个容量为100户的样本,记作①;
某中学高二年级有12名足球运动员,要从中选出3人调查学习负担情况,记作②,
则完成上述2项应采用的抽样方法是____________.
分层随机抽样
简单随机抽样
依据:个体之间是否有明显的差异
练习2:下列问题中,最适合用分层随机抽样抽取样本的是( )
A.从10名同学中抽取3人参加座谈会
B.某政府机关在编人员共100人,其中副处级以上干部10人,一般干部70人,工人20人,上级部门为了了解该机关对政府机构改革的意见,要从中抽取20人,
C.从1 000名工人中,抽取100人调查上班途中所用时间,
D.从生产流水线上,抽取样本检查产品质量
B
依据:个体之间是否有明显的差异
类别 共同点 各自特点 相互联系 适用范围
简单随机抽样 抽样过程中各个个体被抽到的机会相等 从总体中逐个抽取 最基本的抽样方法 总体容量较少
分层抽样 抽样过程中各个个体被抽到的机会相等 将总体分成几部分,每一部分按比例抽取 每层抽样时采用简单随机抽样 总体由差异明显的若干部分组成
总结:简单随机抽样与分层随机抽样的区别
解:(1)因为不同岗位对改革意见有明显的差异,符合分层随机抽样的特点,故选用分层随机抽样方法.
例1.一个单位有职工160人,其中有业务人员112人,管理人员16人,后勤人员32人,为了了解职工对单位改革意见的某种情况,要从中抽取一个容量为20 的样本,
(1)试确定用何种方法抽取 (2)写出抽样过程
解:
第四步:在各层中分别用简单随机抽样抽取业务人员14人;管理人员2人;
后勤人员4人
例1.一个单位有职工160人,其中有业务人员112人,管理人员16人,后勤人员32人,为了了解职工对单位改革意见的某种情况,要从中抽取一个容量为20 的样本,
(1)试确定用何种方法抽取 (2)写出抽样过程
第一步:按业务人员、后勤人员、管理人员分成三层
第二步:计算抽样比:
第三步:确定各层抽取的样本数:
第五步:将所抽取的个体组合在一起构成样本容量为20的样本
分层随机抽样的步骤:
第二步,计算样本容量与总体的个体数比例
第五步,将各层抽取的个体合在一起,就得到所取样本.
第四步,各层用简单随机抽样的方法抽样;
第三步,将总体分层 ,确定第i层应该抽取的个体数目为
求比
定数
抽样
成样
第一步,根据已掌握信息,将总体分成互不相交的层;
分层
归纳:
问题5:我们从树从中学高一年级712名学生中用分层随机抽样抽取了一个容量为50的样本,如何估计高一年级学生的平均身高?
2.总体平均数的估计
即估计树人中学高一年级学生的平均身高在165.2 cm左右.
问题6:一般地,分层随机抽样中,是否可以直接用样本平均数估计总体平均数?
第1层的总体平均数为
第2层的总体平均数为
第1层样本平均数为
第2层样本平均数为
样本平均数为:
2.总体平均数的估计
总体平均数为
2.总体平均数的估计
用比例分配的分层随机抽样方法,从高一年级的学生中抽取了10个样本量为50的样本,计算出样本平均数如下表.
3.探索不同抽样估计总体的效果
序号 1 2 3 4 5 6 7 8 9 10
样本平均数 165.8 165.1 164.3 164.3 166.4 164.6 165.2 164.9 166.1 165.1
问题7:把分层随机抽样的平均数与上一节样本量为50的简单随机抽样的平均数用图形进行表示,通过比较两次的结果,你有什么发现?
探究:从样本均值估计总体均值的角度,分层随机抽样的估计效果是否一定比简单随机抽样的估计效果好呢?
(2)分层随机抽样样本平均数更均匀,简单随机抽样中出现了“极端”的样
本,分层随机抽样中几乎没有出现;
(3)在个体之间差异较大时,只要选取的分层变量合适,分层随机抽样的效果一般会好于简单随机抽样.
(1)与简单随机抽样的结果比较,分层随机抽样并没有明显优于简单随机抽样;
例2.高二年级有男生490人,女生510人,张华按男生、女生进行分层,通过
分层随机抽样的方法,得到男生、女生的平均身高分别为170.2cm和160.8cm.
如果张华在各层中按等比例分配样本,总样本量为100,那么在男生、女生
中分别抽取了多少名?在这种情况下,请估计高二年级全体学生的平均身高.
(教材第185 页第三题)
五.小结
六.作业
人教A版必修第二册:
184页练习1、2、3、4
188页习题9.1第5、7题
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
