黑龙江省大庆市林甸县第一中学2022-2023学年高一下学期期中教学质量检测数学试题(PDF版含解析)
文档属性
| 名称 | 黑龙江省大庆市林甸县第一中学2022-2023学年高一下学期期中教学质量检测数学试题(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 291.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 21:44:24 | ||
图片预览




文档简介
林甸县第一中学 2022-2023学年高一下学期期中教学质量检测
数学试卷
考生注意:
1.本试卷满分 150分,考试时间 120分钟。
2.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用 2B铅笔把答题卡上对
应题目的答案标号涂黑;非选择题请用直径 0.5毫米黑色墨水签字笔在答题卡上各题的答题区域
内作答,超.出.答.题.区.域.书.写.的.答.案.无.效.,.在.试.题.卷.、.草.稿.纸.上.作.答.无.效.。
3.本卷命题范围:必修第一册(第五章),必修第二册(6.1~8.4)。
一、选择题:本大题共 8小题;每小题 5分,共 40分.在每小题给出的四个选项中,只有一个
选项是符合题目要求的.
1.若 a和b 是异面直线, b和 c是异面直线,则 a和 c的位置关系是( )
A.异面或平行 B.异面或相交
C.异面 D.相交、平行或异面
2.设复数 z满足 z z i 2,则 z的虚部为( )
3 3
A. B. i C.1 D. i
4 4
3.某人先向东走3km ,位移记为 a,接着再向北走3km ,位移记为 b,则 a b表示( )
A.向东北走3 2km B.向东南走3 2km
C.向东南走3 3km D.向东北走3 3km
4.函数 f x ln 1 2cos2x 的定义域是( )
2 2 A. k , k
k Z B 2k , 2k . k Z
3 3 3 3
2
C . 2k ,
2
2k k Z D. k ,
k k Z
3 3 3 3
5 2.设m R,则“m 2”是“复数 z m 4 m 1 i为纯虚数”的( )
A.必要而不充分条件 B.充分而不必要条件
C.充分必要条件 D.既不充分也不必要条件
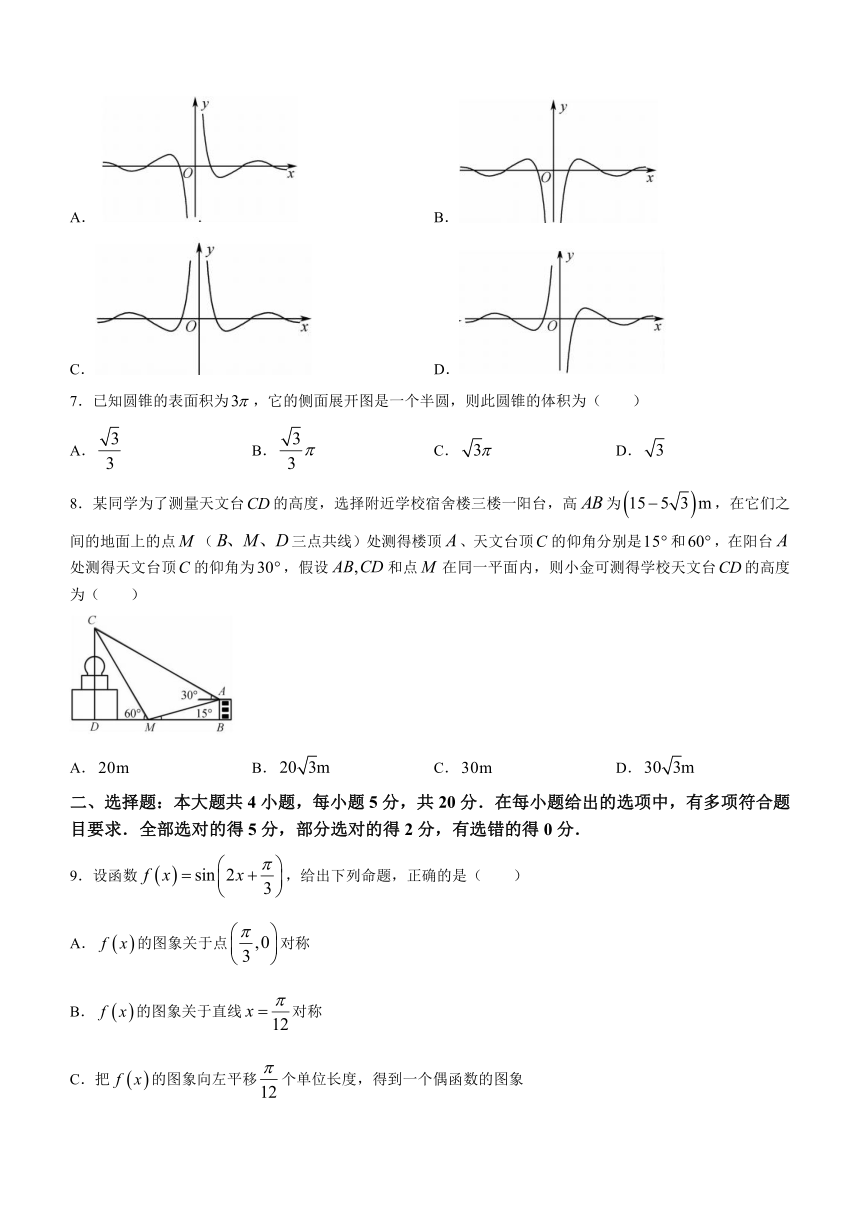
f x 6cosx6.函数 的图象大致为( )
2x sinx
A. B.
C. D.
7.已知圆锥的表面积为3 ,它的侧面展开图是一个半圆,则此圆锥的体积为( )
3 3
A. B. C. 3 D. 3
3 3
8.某同学为了测量天文台CD的高度,选择附近学校宿舍楼三楼一阳台,高 AB为 15 5 3 m,在它们之
间的地面上的点M ( B、M、D三点共线)处测得楼顶 A、天文台顶C的仰角分别是15 和60 ,在阳台 A
处测得天文台顶C的仰角为30 ,假设 AB,CD和点M 在同一平面内,则小金可测得学校天文台CD的高度
为( )
A.20m B. 20 3m C.30m D.30 3m
二、选择题:本大题共 4小题,每小题 5分,共 20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
9 .设函数 f x sin 2x
,给出下列命题,正确的是( )
3
A. f x ,0 的图象关于点 对称
3
B. f x 的图象关于直线 x 对称
12
C.把 f x 的图象向左平移 个单位长度,得到一个偶函数的图象
12
D. f x 的最小正周期为 ,且在 0, 上为增函数 6
10.设直线 l不在平面 内,直线m 在平面 内,则下列说法不正确的是( )
A.直线 l与直线m 没有公共点 B.直线 l与直线m 异面
C.直线 l与直线m 至多一个公共点 D.直线 l与直线m 不垂直
11.一半径为 4米的水轮如图所示,水轮圆心O距离水面 2米,已知水轮每 30秒逆时针匀速转动一圈,如果
当水轮上点P从水中浮现时(图中点 P0)开始计时,则( )
A.点 P第一次到达最高点需要 10秒
B.当水轮转动 35秒时,点 P距离水面 2米
C.当水轮转动 25秒时,点 P在水面下方,距离水面 2米
D
.点 P距离水面的高度 h(米)与 t(秒)的函数解析式为h 4sin t 2
30 6
12.已知函数 f x sin x cosx ,下列关于此函数的论述正确的是( )
A. 是 f x 的一个周期 B.函数 f x 的值域为 2,1
3 4
C .函数 f x 在 , 上单调递减 D.函数 f x 在 2 , 2 内有 4个零点 4 3
三、填空题:本大题共 4小题,每小题 5分,共 20分.
13 2.关于 x的不等式 x ax b 0的解集为 2,1 ,则复数a bi所对应的点位于复平面内的第________
象限.
14 .已知 0, , tan 2,则 cos
________.
2 4
15.如图所示,△ABC 中,AC 12cm,边 AC上的高 BD 12cm,则其水平放置的直观图的面积为________.
16.在钝角△ABC 中,角 A,B,C 的对边分别为 a,b,c,a 4,sinA 2sinB sinC ,则边 b 的取值范围是
________.
四、解答题:本大题共 6小题,共 70分.解答应写出必要的文字说明、证明过程及演算步骤.
17.(10分)
如图,棱锥的底面 ABCD 是一个矩形, AC 与 BD 交于点 M ,VM 是棱锥的高.若 VM 4cm ,
AB 4cm,VC 5cm,求锥体的体积.
18.(12分)
(1)已知复数 1 3i是关于 x的方程 x2 px q 0 p,q R 的一个根,求 p q的值;
1 1 1
(2)已知复数 z1 5 10i, z2 3 4i, ,求 z .z z1 z2
19.(12分)
(1)直线 a和两条异面直线b,c都相交,画出每两条相交直线所确定的平面,并标上字母;
(2)如图,已知 A,B,C,D是空间四点,且点 A,B,C 在同一直线 l 上,点 D 不在直线 l 上.求证:直线
AD,BD,CD在同一平面内.
20.(12分)
已知平面内的三个向量 a 3,2 ,b 1,2 ,c 4,1 .
(1)若 a b c , R ,求 的值;
(2)若向量 a kb与向量2b c共线,求实数 k 的值.
21.(12分)
如图为函数 f x Asin x A 0, 0,
, x R
2
的部分图象.
(1)求函数解析式;
3
(2)已知 f , 0, ,求 的取值范围;
2
3
(3 )若方程 f x m在 0, 上有两个不相等的实数根,求实数m 的取值范围. 4
22.(12分)
已知 a,b,c分别是△ABC 三个内角 A,B,C 的对边,且 3asinC ccosA c.
(1)求角 A的大小;
a b
(2)若 c a,求m 的取值范围.
c
林甸县第一中学 2022-2023学年高一下学期期中教学质量检测
数学
参考答案、提示及评分细则
1.D 异面直线不具有传递性,可以以长方体为载体加以说明,a,b异面,直线 c的位置可如图所示.
2 . C 解 : 设 复 数 z x yi, x, y R , 由 z z i 2 , 得 x yi x2 y2 i 2 , 即
(x x2 y2 yi 2 i;所以 y 1,即 z的虚部为 1.
3.A 由题意和向量的加法,得a b表示先向东走3km ,再向北走3km ,即向东北走3 2km.
1 2 2
4 . D 依 题 意 , 1 2cos2x 0 , 即 cos2x , 2k 2x 2k ,k Z , 解 得 :
2 3 3
k x k k Z, f x ln 1 2cos2x k , k , 函数 的定义域是 k Z .3 3 3 3
2
5 B 2. 复数 z m 4 m 1 i m 4 0,为纯虚数, 解得m 2或 2, m R,则“m 2”
m 1 0,
是“复数 z m2 4 m 1 i为纯虚数”的充分不必要条件.
6cosx
6.A 函数 f x 为奇函数,所以排除选项 B,C;又当 x 0时, f x 第一个零点为 x ,
2x sinx 2
x 2 2 所以令 ,则有2x sinx 0,cos 0,所以 f 0,排除 D.
4 2 4 2 4
7 B 2 2. 设圆锥的底面半径为 r,圆锥的母线长为 l,由 l 2 r,得 l 2r,又 S r r 2r 3 r 3 ,
2
所 以 r 1 , 解 得 r 1 ; 所 以 圆 锥 的 高 为 h l 2 r2 22 12 3 , 所 以 圆 锥 的 体 积 为
V 1 1 r2h 3 12 3
3 3 3
7 AM CM
8.C 由题意, CAM , AMC ,即 ACM ,所以△CAM 中, ,
4 12 6 sin ACM sin CAM
则CM AM sin CAM AM AB,而 ,
sin ACM sin
12
5 3 3 sin 3
因为在△CDM 中,CD CM sin 4 30米.3 sin sin 2
6 12
9 .ABC 因为 f sin 0
,所以 A正确;因为 f
3 12
sin 1,所以 B正确;因为函数 f x 的
2
f sin 1 3 最小正周期为 ,但 f
,所以 D不正确;把函数 f x 的图象向左平移 个
12 2 2 6 12
单位长度,得到函数 y sin 2 x sin 2x cos2x 的图象,函数 y cos2x为偶函数,
12 3 2
所以 C正确.故选 ABC.
10.ABD 对于选项 A,直线 l不在平面 内,直线m 在平面 内,但是,直线 l与m 可以相交,故 A错误;
对于选项 B,直线 l不在平面 内,直线m 在平面 内,但是,直线 l与m 可以相交也可以平行,故 B错误;
对于选项 C,直线 l不在平面 内,直线m 在平面 内,则直线 l与直线m 只可以平行或者相交,不可能重
合,所以,直线 l与直线m 至多一个公共点,故 C正确;对于选项 D,直线 l不在平面 内,直线m 在平面
内,则当直线 l垂直于平面 时,直线 l与直线m 垂直,故 D错误.
11 . AC 设 点 P 距 离 水 面 的 高 度 h ( 米 ) 和 时 间 t ( 秒 ) 的 函 数 解 析 式 为
hmax A B 6,
hmin A B 2,
h Asin t B A 0, 0,
,由题意得: 2
2 T 30,
h 0 Asin 0 B 0,
A 4,
B 2,
解得: 2 , h 4sin t 2.故 D错误;
T 15 15 6
,
6
6 4sin t 2 sin t 对于 A.令h 6,即 ,即 1,
t ,解得:t 10,故 A对;
15 6 15 6 15 6 2
对于 B ,令 t 35,代入 h 4sin t 2,解得: h 4,故 B 错误;对于 C.令 t 25,代入
15 6
h 4sin t
2,解得: h 2,故 C对.
15 6
12.BCD 选项 A:因为 f 4
0 f 2, 不是 f x 的一个周期,故 A错误;选项 B,D:
4
函数 f x 定义域为R ,并且 f x f x ,所以函数为偶函数;因为 x 0, , f x f x 2 ,
3
为周期函数,故仅需研究函数 f x 在区间 0,2 上的值域及零点个数即可,因为 x 0, ,2 时, 2 2
f x sinx cosx 2sin x
x , 3 f x sinx cosx 2sin x ; 当 时 , ; 当
4 2 2 4
x 0, 3 ,2 时,令 x t
,
5 , 7 ,则 y 2 sin t, t
, 5 , 7 ,
2 2 4 4 4 4 4 4 4 4 4
y 2,1 x , 3 可得
且仅一个零点;当 时,令 x
t 3 , 7 3 7
2 2 4 4 4
,则 y 2sint, t , , 4 4
可得 y 2,1 且仅一个零点;所以函数 f x 的值域为 2,1 且在 2 , 2 上有 4个零点.故选项 B,
3 , 4 f x 19 D正确.选项 C:函数 f x 在 上,有 sinx cosx 2sin
x ,所以 x , ,
4 3 4 4 12
则得函数 f x 在该区间上为单调减函数.故选项 C正确.
2 2 1 a,13.二 ∵不等式 x ax b 0的解集为 2,1 ,∴由一元二次方程根与系数的关系,得
2 1 b,
a 1,
解得 即 a 0,b 0,故复数 a bi所对应的点位于复平面内的第二象限.
b 2,
3 10 1
14. 由 tan 2,得 sin 2cos ,又 sin2 cos2 1, cos2 ,
10 5
0, , cos
5
,sin 2 5 ,因为 cos cos cos
sin sin ,
2 5 5 4 4 4
cos 5 2 2 5 2 3 10 .
4 5 2 5 2 10
15.18 2cm2 根据题意,设△ABC 的水平放置的直观图的面积为 S,原图△ABC 中, AC 12cm,边
1 S 2 2
AC 2 2上的高 BD 12cm,则 S△ABC 12 12 72cm ,则有 ,则 S 72 18 2cm .2 S△ABC 4 4
8 16 16 b2 c2 a2 ,
16 . , ,8
由 sinA 2sinB sinC ,得 a 2b c .①当 A为针角,则 即
3 5 3 b c a,
b2 (2b 4)2 16, 8 16 a2 b2 c2 , b 16 b
2 (2b 4)2 ,
解得 ;②当 C 为钝角,则b 2b
即 解得
4 4, 3 5 a b c, 4 b 2b 4,
16 8 16 16
b 8.综上, b 的取值范围是 , ,8
3 3 5 3
.
17.解:因为VM 是棱锥的高,所以VM MC .
在Rt△VMC中,MC VC 2 VM 2 52 42 3 cm ,所 AC 2MC 6 cm .
在Rt△ABC 中, BC AC 2 AB2 62 42 2 5 cm .
S AB BC 4 2 5 8 5 cm2底 ,
V 1 S h 1 8 5 4 32 5所以 锥 底 cm3 .3 3 3
32 5 3
所以棱锥的体积为 cm .
3
18 2.解:(1)因为 1 3i是方程 x px q 0的一个根,
(3i 1)2 p 3i 1 q 0,
8 p q 3p 6 i 0,而 p,q R,
8 p q 0,
3p 6 0,
p 2,
∴ p q 12.
q 10,
(2) z 1 1 1 z1 z21 5 10i, z2 3 4i, ,z z1 z2 z1z2
z z1z2 5 10i 3 4i 55 10i 55 10i 8 6i 500 250i 5 5 i,
z1 z2 8 6i 8 6i 8 6i 8 6i 100 2
2
z 52 5 5 5 .
2 2
19.(1)解:根据题意,画出的图形如图所示:
直线 a和直线 b所确定的平面为 ,直线 a直线 c所确定的平面为 .
(2)证明:因为点 A,B,C 在同一直线 l上,点D不在直线 l上,所以点 A,B,D确定唯一的一个平面,设为 ,
所以 l ,因为C l ,所以C ,所以 A,B,C,D ,
所以 AD ,BD ,CD ,即直线 AD,BD,CD在同一平面内.
20.解:(1) b ,2 , c 4 , ,
b c 4 ,2 .
4 3,
又a b c,
2 2,
5 , 9 1
解得 ∴ .
8 , 3
9
(2)a kb 3 k ,2 2k ,2b c 6,3 .
a kb与2b c共线,
7
3 3 k 6 2 2k ,解得 k .
3
T
21.解:(1)由题意可知, A 1, , T , 2.
4 4
7 7 函数图象过点 , 1 , sin 1.
12 6
2k ,k Z, , , f x sin 2x .3 2 3 3
f 3 2 (2) , 2k 2 2k ,k Z,
2 3 3 3
k k ,k Z.
6
0, , 0 .
6
2k (3)令 2x 2k ,k Z, 5 k x k ,k Z.
2 3 2 12 12
x 0, 3 , f x 0, , 7 7 3 在 上为增,在 上为减,在 , 上为增. 4 12 12 12 12 4
作出 f x sin 2x 在区间 0,
3
3 4
上的图象.
f x sin 2x f x m 1 3有两个零点,即 与 y m有两个交点. 1 m 或 m 1.
3 2 2
22.解:(1)在△ABC 中, 3asinC ccosA c,
由正弦定理可得, 3sinAsinC sinCcosA sinC, sinC 0 ,
则 3sinA cosA 1.
即 3sinA 3 cosA 2 sinA
1
cosA 1,
2 2
sin A 1 ,又 A 0, ,解得 A .
6 2 3
( 2 ) 由
3 sin 2 C 3 3 1 3
m a b sinA sinB 2
3 cosC sinC 1 cosC 1 2 2 2 2
c sinC sinC sinC sinC 2
3cos2 C 3cosC
2 1 2 1 3 1C .2sin cosC 2 2sinC 2 2tanC 2
2 2 2 2
C B C 2 C 2 C 3 C因为 c a,所以 ,又 ,所以 ,所以 ,得 tan 3,所
3 3 3 3 6 2 3 3 2
3 1
以 C 3,所以1 m 2.3 tan
2
数学试卷
考生注意:
1.本试卷满分 150分,考试时间 120分钟。
2.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用 2B铅笔把答题卡上对
应题目的答案标号涂黑;非选择题请用直径 0.5毫米黑色墨水签字笔在答题卡上各题的答题区域
内作答,超.出.答.题.区.域.书.写.的.答.案.无.效.,.在.试.题.卷.、.草.稿.纸.上.作.答.无.效.。
3.本卷命题范围:必修第一册(第五章),必修第二册(6.1~8.4)。
一、选择题:本大题共 8小题;每小题 5分,共 40分.在每小题给出的四个选项中,只有一个
选项是符合题目要求的.
1.若 a和b 是异面直线, b和 c是异面直线,则 a和 c的位置关系是( )
A.异面或平行 B.异面或相交
C.异面 D.相交、平行或异面
2.设复数 z满足 z z i 2,则 z的虚部为( )
3 3
A. B. i C.1 D. i
4 4
3.某人先向东走3km ,位移记为 a,接着再向北走3km ,位移记为 b,则 a b表示( )
A.向东北走3 2km B.向东南走3 2km
C.向东南走3 3km D.向东北走3 3km
4.函数 f x ln 1 2cos2x 的定义域是( )
2 2 A. k , k
k Z B 2k , 2k . k Z
3 3 3 3
2
C . 2k ,
2
2k k Z D. k ,
k k Z
3 3 3 3
5 2.设m R,则“m 2”是“复数 z m 4 m 1 i为纯虚数”的( )
A.必要而不充分条件 B.充分而不必要条件
C.充分必要条件 D.既不充分也不必要条件
f x 6cosx6.函数 的图象大致为( )
2x sinx
A. B.
C. D.
7.已知圆锥的表面积为3 ,它的侧面展开图是一个半圆,则此圆锥的体积为( )
3 3
A. B. C. 3 D. 3
3 3
8.某同学为了测量天文台CD的高度,选择附近学校宿舍楼三楼一阳台,高 AB为 15 5 3 m,在它们之
间的地面上的点M ( B、M、D三点共线)处测得楼顶 A、天文台顶C的仰角分别是15 和60 ,在阳台 A
处测得天文台顶C的仰角为30 ,假设 AB,CD和点M 在同一平面内,则小金可测得学校天文台CD的高度
为( )
A.20m B. 20 3m C.30m D.30 3m
二、选择题:本大题共 4小题,每小题 5分,共 20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
9 .设函数 f x sin 2x
,给出下列命题,正确的是( )
3
A. f x ,0 的图象关于点 对称
3
B. f x 的图象关于直线 x 对称
12
C.把 f x 的图象向左平移 个单位长度,得到一个偶函数的图象
12
D. f x 的最小正周期为 ,且在 0, 上为增函数 6
10.设直线 l不在平面 内,直线m 在平面 内,则下列说法不正确的是( )
A.直线 l与直线m 没有公共点 B.直线 l与直线m 异面
C.直线 l与直线m 至多一个公共点 D.直线 l与直线m 不垂直
11.一半径为 4米的水轮如图所示,水轮圆心O距离水面 2米,已知水轮每 30秒逆时针匀速转动一圈,如果
当水轮上点P从水中浮现时(图中点 P0)开始计时,则( )
A.点 P第一次到达最高点需要 10秒
B.当水轮转动 35秒时,点 P距离水面 2米
C.当水轮转动 25秒时,点 P在水面下方,距离水面 2米
D
.点 P距离水面的高度 h(米)与 t(秒)的函数解析式为h 4sin t 2
30 6
12.已知函数 f x sin x cosx ,下列关于此函数的论述正确的是( )
A. 是 f x 的一个周期 B.函数 f x 的值域为 2,1
3 4
C .函数 f x 在 , 上单调递减 D.函数 f x 在 2 , 2 内有 4个零点 4 3
三、填空题:本大题共 4小题,每小题 5分,共 20分.
13 2.关于 x的不等式 x ax b 0的解集为 2,1 ,则复数a bi所对应的点位于复平面内的第________
象限.
14 .已知 0, , tan 2,则 cos
________.
2 4
15.如图所示,△ABC 中,AC 12cm,边 AC上的高 BD 12cm,则其水平放置的直观图的面积为________.
16.在钝角△ABC 中,角 A,B,C 的对边分别为 a,b,c,a 4,sinA 2sinB sinC ,则边 b 的取值范围是
________.
四、解答题:本大题共 6小题,共 70分.解答应写出必要的文字说明、证明过程及演算步骤.
17.(10分)
如图,棱锥的底面 ABCD 是一个矩形, AC 与 BD 交于点 M ,VM 是棱锥的高.若 VM 4cm ,
AB 4cm,VC 5cm,求锥体的体积.
18.(12分)
(1)已知复数 1 3i是关于 x的方程 x2 px q 0 p,q R 的一个根,求 p q的值;
1 1 1
(2)已知复数 z1 5 10i, z2 3 4i, ,求 z .z z1 z2
19.(12分)
(1)直线 a和两条异面直线b,c都相交,画出每两条相交直线所确定的平面,并标上字母;
(2)如图,已知 A,B,C,D是空间四点,且点 A,B,C 在同一直线 l 上,点 D 不在直线 l 上.求证:直线
AD,BD,CD在同一平面内.
20.(12分)
已知平面内的三个向量 a 3,2 ,b 1,2 ,c 4,1 .
(1)若 a b c , R ,求 的值;
(2)若向量 a kb与向量2b c共线,求实数 k 的值.
21.(12分)
如图为函数 f x Asin x A 0, 0,
, x R
2
的部分图象.
(1)求函数解析式;
3
(2)已知 f , 0, ,求 的取值范围;
2
3
(3 )若方程 f x m在 0, 上有两个不相等的实数根,求实数m 的取值范围. 4
22.(12分)
已知 a,b,c分别是△ABC 三个内角 A,B,C 的对边,且 3asinC ccosA c.
(1)求角 A的大小;
a b
(2)若 c a,求m 的取值范围.
c
林甸县第一中学 2022-2023学年高一下学期期中教学质量检测
数学
参考答案、提示及评分细则
1.D 异面直线不具有传递性,可以以长方体为载体加以说明,a,b异面,直线 c的位置可如图所示.
2 . C 解 : 设 复 数 z x yi, x, y R , 由 z z i 2 , 得 x yi x2 y2 i 2 , 即
(x x2 y2 yi 2 i;所以 y 1,即 z的虚部为 1.
3.A 由题意和向量的加法,得a b表示先向东走3km ,再向北走3km ,即向东北走3 2km.
1 2 2
4 . D 依 题 意 , 1 2cos2x 0 , 即 cos2x , 2k 2x 2k ,k Z , 解 得 :
2 3 3
k x k k Z, f x ln 1 2cos2x k , k , 函数 的定义域是 k Z .3 3 3 3
2
5 B 2. 复数 z m 4 m 1 i m 4 0,为纯虚数, 解得m 2或 2, m R,则“m 2”
m 1 0,
是“复数 z m2 4 m 1 i为纯虚数”的充分不必要条件.
6cosx
6.A 函数 f x 为奇函数,所以排除选项 B,C;又当 x 0时, f x 第一个零点为 x ,
2x sinx 2
x 2 2 所以令 ,则有2x sinx 0,cos 0,所以 f 0,排除 D.
4 2 4 2 4
7 B 2 2. 设圆锥的底面半径为 r,圆锥的母线长为 l,由 l 2 r,得 l 2r,又 S r r 2r 3 r 3 ,
2
所 以 r 1 , 解 得 r 1 ; 所 以 圆 锥 的 高 为 h l 2 r2 22 12 3 , 所 以 圆 锥 的 体 积 为
V 1 1 r2h 3 12 3
3 3 3
7 AM CM
8.C 由题意, CAM , AMC ,即 ACM ,所以△CAM 中, ,
4 12 6 sin ACM sin CAM
则CM AM sin CAM AM AB,而 ,
sin ACM sin
12
5 3 3 sin 3
因为在△CDM 中,CD CM sin 4 30米.3 sin sin 2
6 12
9 .ABC 因为 f sin 0
,所以 A正确;因为 f
3 12
sin 1,所以 B正确;因为函数 f x 的
2
f sin 1 3 最小正周期为 ,但 f
,所以 D不正确;把函数 f x 的图象向左平移 个
12 2 2 6 12
单位长度,得到函数 y sin 2 x sin 2x cos2x 的图象,函数 y cos2x为偶函数,
12 3 2
所以 C正确.故选 ABC.
10.ABD 对于选项 A,直线 l不在平面 内,直线m 在平面 内,但是,直线 l与m 可以相交,故 A错误;
对于选项 B,直线 l不在平面 内,直线m 在平面 内,但是,直线 l与m 可以相交也可以平行,故 B错误;
对于选项 C,直线 l不在平面 内,直线m 在平面 内,则直线 l与直线m 只可以平行或者相交,不可能重
合,所以,直线 l与直线m 至多一个公共点,故 C正确;对于选项 D,直线 l不在平面 内,直线m 在平面
内,则当直线 l垂直于平面 时,直线 l与直线m 垂直,故 D错误.
11 . AC 设 点 P 距 离 水 面 的 高 度 h ( 米 ) 和 时 间 t ( 秒 ) 的 函 数 解 析 式 为
hmax A B 6,
hmin A B 2,
h Asin t B A 0, 0,
,由题意得: 2
2 T 30,
h 0 Asin 0 B 0,
A 4,
B 2,
解得: 2 , h 4sin t 2.故 D错误;
T 15 15 6
,
6
6 4sin t 2 sin t 对于 A.令h 6,即 ,即 1,
t ,解得:t 10,故 A对;
15 6 15 6 15 6 2
对于 B ,令 t 35,代入 h 4sin t 2,解得: h 4,故 B 错误;对于 C.令 t 25,代入
15 6
h 4sin t
2,解得: h 2,故 C对.
15 6
12.BCD 选项 A:因为 f 4
0 f 2, 不是 f x 的一个周期,故 A错误;选项 B,D:
4
函数 f x 定义域为R ,并且 f x f x ,所以函数为偶函数;因为 x 0, , f x f x 2 ,
3
为周期函数,故仅需研究函数 f x 在区间 0,2 上的值域及零点个数即可,因为 x 0, ,2 时, 2 2
f x sinx cosx 2sin x
x , 3 f x sinx cosx 2sin x ; 当 时 , ; 当
4 2 2 4
x 0, 3 ,2 时,令 x t
,
5 , 7 ,则 y 2 sin t, t
, 5 , 7 ,
2 2 4 4 4 4 4 4 4 4 4
y 2,1 x , 3 可得
且仅一个零点;当 时,令 x
t 3 , 7 3 7
2 2 4 4 4
,则 y 2sint, t , , 4 4
可得 y 2,1 且仅一个零点;所以函数 f x 的值域为 2,1 且在 2 , 2 上有 4个零点.故选项 B,
3 , 4 f x 19 D正确.选项 C:函数 f x 在 上,有 sinx cosx 2sin
x ,所以 x , ,
4 3 4 4 12
则得函数 f x 在该区间上为单调减函数.故选项 C正确.
2 2 1 a,13.二 ∵不等式 x ax b 0的解集为 2,1 ,∴由一元二次方程根与系数的关系,得
2 1 b,
a 1,
解得 即 a 0,b 0,故复数 a bi所对应的点位于复平面内的第二象限.
b 2,
3 10 1
14. 由 tan 2,得 sin 2cos ,又 sin2 cos2 1, cos2 ,
10 5
0, , cos
5
,sin 2 5 ,因为 cos cos cos
sin sin ,
2 5 5 4 4 4
cos 5 2 2 5 2 3 10 .
4 5 2 5 2 10
15.18 2cm2 根据题意,设△ABC 的水平放置的直观图的面积为 S,原图△ABC 中, AC 12cm,边
1 S 2 2
AC 2 2上的高 BD 12cm,则 S△ABC 12 12 72cm ,则有 ,则 S 72 18 2cm .2 S△ABC 4 4
8 16 16 b2 c2 a2 ,
16 . , ,8
由 sinA 2sinB sinC ,得 a 2b c .①当 A为针角,则 即
3 5 3 b c a,
b2 (2b 4)2 16, 8 16 a2 b2 c2 , b 16 b
2 (2b 4)2 ,
解得 ;②当 C 为钝角,则b 2b
即 解得
4 4, 3 5 a b c, 4 b 2b 4,
16 8 16 16
b 8.综上, b 的取值范围是 , ,8
3 3 5 3
.
17.解:因为VM 是棱锥的高,所以VM MC .
在Rt△VMC中,MC VC 2 VM 2 52 42 3 cm ,所 AC 2MC 6 cm .
在Rt△ABC 中, BC AC 2 AB2 62 42 2 5 cm .
S AB BC 4 2 5 8 5 cm2底 ,
V 1 S h 1 8 5 4 32 5所以 锥 底 cm3 .3 3 3
32 5 3
所以棱锥的体积为 cm .
3
18 2.解:(1)因为 1 3i是方程 x px q 0的一个根,
(3i 1)2 p 3i 1 q 0,
8 p q 3p 6 i 0,而 p,q R,
8 p q 0,
3p 6 0,
p 2,
∴ p q 12.
q 10,
(2) z 1 1 1 z1 z21 5 10i, z2 3 4i, ,z z1 z2 z1z2
z z1z2 5 10i 3 4i 55 10i 55 10i 8 6i 500 250i 5 5 i,
z1 z2 8 6i 8 6i 8 6i 8 6i 100 2
2
z 52 5 5 5 .
2 2
19.(1)解:根据题意,画出的图形如图所示:
直线 a和直线 b所确定的平面为 ,直线 a直线 c所确定的平面为 .
(2)证明:因为点 A,B,C 在同一直线 l上,点D不在直线 l上,所以点 A,B,D确定唯一的一个平面,设为 ,
所以 l ,因为C l ,所以C ,所以 A,B,C,D ,
所以 AD ,BD ,CD ,即直线 AD,BD,CD在同一平面内.
20.解:(1) b ,2 , c 4 , ,
b c 4 ,2 .
4 3,
又a b c,
2 2,
5 , 9 1
解得 ∴ .
8 , 3
9
(2)a kb 3 k ,2 2k ,2b c 6,3 .
a kb与2b c共线,
7
3 3 k 6 2 2k ,解得 k .
3
T
21.解:(1)由题意可知, A 1, , T , 2.
4 4
7 7 函数图象过点 , 1 , sin 1.
12 6
2k ,k Z, , , f x sin 2x .3 2 3 3
f 3 2 (2) , 2k 2 2k ,k Z,
2 3 3 3
k k ,k Z.
6
0, , 0 .
6
2k (3)令 2x 2k ,k Z, 5 k x k ,k Z.
2 3 2 12 12
x 0, 3 , f x 0, , 7 7 3 在 上为增,在 上为减,在 , 上为增. 4 12 12 12 12 4
作出 f x sin 2x 在区间 0,
3
3 4
上的图象.
f x sin 2x f x m 1 3有两个零点,即 与 y m有两个交点. 1 m 或 m 1.
3 2 2
22.解:(1)在△ABC 中, 3asinC ccosA c,
由正弦定理可得, 3sinAsinC sinCcosA sinC, sinC 0 ,
则 3sinA cosA 1.
即 3sinA 3 cosA 2 sinA
1
cosA 1,
2 2
sin A 1 ,又 A 0, ,解得 A .
6 2 3
( 2 ) 由
3 sin 2 C 3 3 1 3
m a b sinA sinB 2
3 cosC sinC 1 cosC 1 2 2 2 2
c sinC sinC sinC sinC 2
3cos2 C 3cosC
2 1 2 1 3 1C .2sin cosC 2 2sinC 2 2tanC 2
2 2 2 2
C B C 2 C 2 C 3 C因为 c a,所以 ,又 ,所以 ,所以 ,得 tan 3,所
3 3 3 3 6 2 3 3 2
3 1
以 C 3,所以1 m 2.3 tan
2
同课章节目录
