抛物线的几何性质(一)
图片预览





文档简介
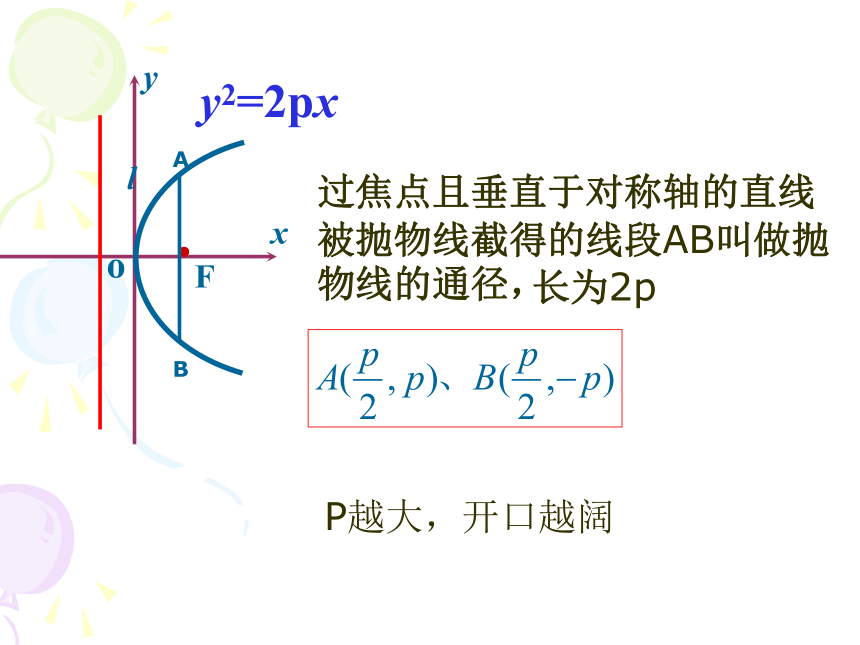
课件17张PPT。抛物线的简单几何性质(二)y2=2pxlAB过焦点且垂直于对称轴的直线被抛物线截得的线段AB叫做抛物线的通径,长为2pP越大,开口越阔关于x 轴
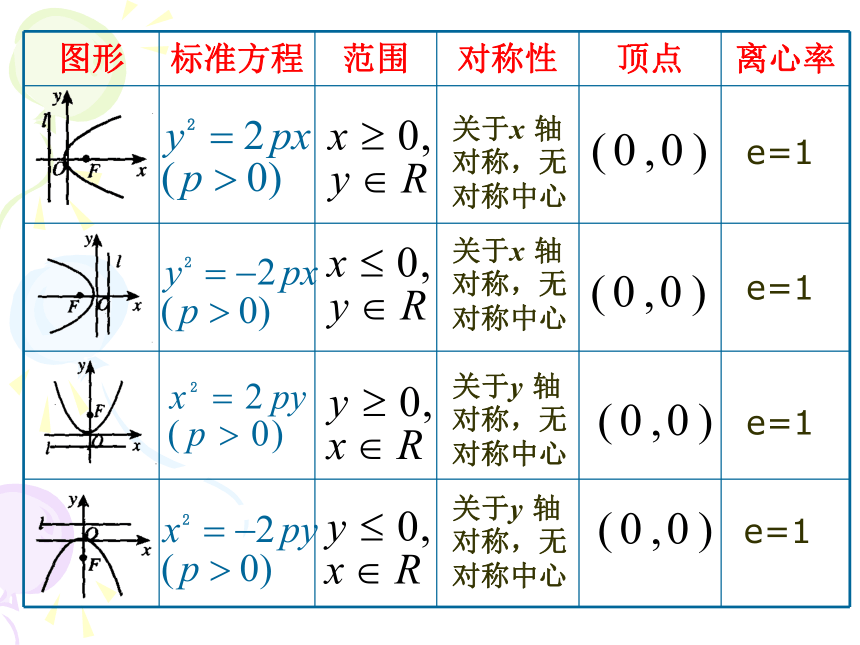
对称,无
对称中心关于x 轴
对称,无
对称中心关于y 轴
对称,无
对称中心关于y 轴
对称,无
对称中心e=1e=1e=1e=1抛物线的几何性质特点(1)只位于半个坐标平面内,虽然它可以无限延伸,但没有渐进线。(2)只有一条对称轴,没有对称中心。(3)只有一个顶点,一个焦点,一条准线。(4)离心率e是确定的,即e =1 (5)一次项系数的绝对值越大,开口越大例4、已知AB是抛物线y2=2px的任意一条焦点弦,且A(x1,y1)、B(x2,y2)(1)求证:y1y2=-P2,x1x2=p2/4。(2)若弦AB被焦点分成长为m,n的两部分,求证:1/m+1/n=2/p。(3)设θ为直线AB的倾斜角,求证:当θ=90o时,取得︱AB︱的最小值2p。(4)求证:焦点F对A、B在准线上射影的张角为90o。(5)若弦AB过焦点,求证:以AB为直径的圆与准线相切。
(4)过抛物线
的焦点F的直线与抛物线
相交于A,B两点,自A、B
向准线作垂线,垂足分别
为C、D,求证:125346证明:如图,由抛物线定义知|AF|=|AC|,
所以 。
同理, 。又AC//BD,
因为
所以
则 ,
可证 变式1
若在上题的条件中,以线段CD为直径的圆有与点F有什么关系?分析:运用抛物线的定义和平面几何知识来证比较简捷. (5) 过抛物线y2=2px的焦点F任作一条直线m,
交这抛物线于A、B两点,求证:以AB为直径的圆
和这抛物线的准线相切.证明:如图. 所以EH是以AB为直径的圆E的半径,且EH⊥l,因而圆E和准线l相切.设AB的中点为E,过A、E、B分别向准线l引垂线AD,EH,BC,垂足为D、H、C,则|AF|=|AD|,|BF|=|BC|∴|AB|=|AF|+|BF|
=|AD|+|BC|=2|EH|课堂小结
(1)抛物线的简单几何性质
(2)抛物线与椭圆、双曲线几何性质的不同点
(3)应用性质求标准方程的方法和步骤
对称,无
对称中心关于x 轴
对称,无
对称中心关于y 轴
对称,无
对称中心关于y 轴
对称,无
对称中心e=1e=1e=1e=1抛物线的几何性质特点(1)只位于半个坐标平面内,虽然它可以无限延伸,但没有渐进线。(2)只有一条对称轴,没有对称中心。(3)只有一个顶点,一个焦点,一条准线。(4)离心率e是确定的,即e =1 (5)一次项系数的绝对值越大,开口越大例4、已知AB是抛物线y2=2px的任意一条焦点弦,且A(x1,y1)、B(x2,y2)(1)求证:y1y2=-P2,x1x2=p2/4。(2)若弦AB被焦点分成长为m,n的两部分,求证:1/m+1/n=2/p。(3)设θ为直线AB的倾斜角,求证:当θ=90o时,取得︱AB︱的最小值2p。(4)求证:焦点F对A、B在准线上射影的张角为90o。(5)若弦AB过焦点,求证:以AB为直径的圆与准线相切。
(4)过抛物线
的焦点F的直线与抛物线
相交于A,B两点,自A、B
向准线作垂线,垂足分别
为C、D,求证:125346证明:如图,由抛物线定义知|AF|=|AC|,
所以 。
同理, 。又AC//BD,
因为
所以
则 ,
可证 变式1
若在上题的条件中,以线段CD为直径的圆有与点F有什么关系?分析:运用抛物线的定义和平面几何知识来证比较简捷. (5) 过抛物线y2=2px的焦点F任作一条直线m,
交这抛物线于A、B两点,求证:以AB为直径的圆
和这抛物线的准线相切.证明:如图. 所以EH是以AB为直径的圆E的半径,且EH⊥l,因而圆E和准线l相切.设AB的中点为E,过A、E、B分别向准线l引垂线AD,EH,BC,垂足为D、H、C,则|AF|=|AD|,|BF|=|BC|∴|AB|=|AF|+|BF|
=|AD|+|BC|=2|EH|课堂小结
(1)抛物线的简单几何性质
(2)抛物线与椭圆、双曲线几何性质的不同点
(3)应用性质求标准方程的方法和步骤
