1.1探索勾股定理(2)同步练习(含答案) 2023—2024学年北师大版数学八年级上册
文档属性
| 名称 | 1.1探索勾股定理(2)同步练习(含答案) 2023—2024学年北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 117.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 13:25:42 | ||
图片预览


文档简介
北师大版数学八年级上册 第一章 勾股定理
1.2 探索勾股定理
一、选择题。
1.利用四个全等的直角三角形可以拼成如图所示的图形.通过该图形,可以验证公式( )
A.(a+b)(a-b)=a2-b2
B.(a+b)2=a2+2ab+b2
C.c2=a2+b2
D.(a-b)2=a2-2ab+b2
2.(2021·新疆乌鲁木齐模拟)直角三角形中,一条直角边长为24 cm,斜边长为25 cm,则另一直角边长为 ( )
A.7 cm B.12 cm C.16 cm D.49 cm
3.如图,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA,BC为半径的两个圆形成一圆环.该圆环的面积为( )
A.π B.3π C.9π D.6π
4.如图,韩彬同学从位于超市南偏西30°的家(记作A)出发行走了4 000 m到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3 000 m到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
A.2 000 m B.3 000 m C.4 000 m D.5 000 m
5.(2021·甘肃张掖期中)如图,在由边长为1个单位长度的小正方形组成的网格中,点A, B都是格点,则线段AB的长为 ( )
A.5 B. 6 C.7 D.2
6.(2021·宁夏银川期中)若直角三角形的两直角边长分别为5 cm,12 cm,则斜边上的高为 ( )
A. cm B. cm C.13 cm D. cm
7.如图,公园内有一个长方形草坪,有少数人为避开直角走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了________路(假设2步为1 m)( )
A.1步 B.2步
C.3步 D.4步
8.(2019秋 昌平区期末)如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
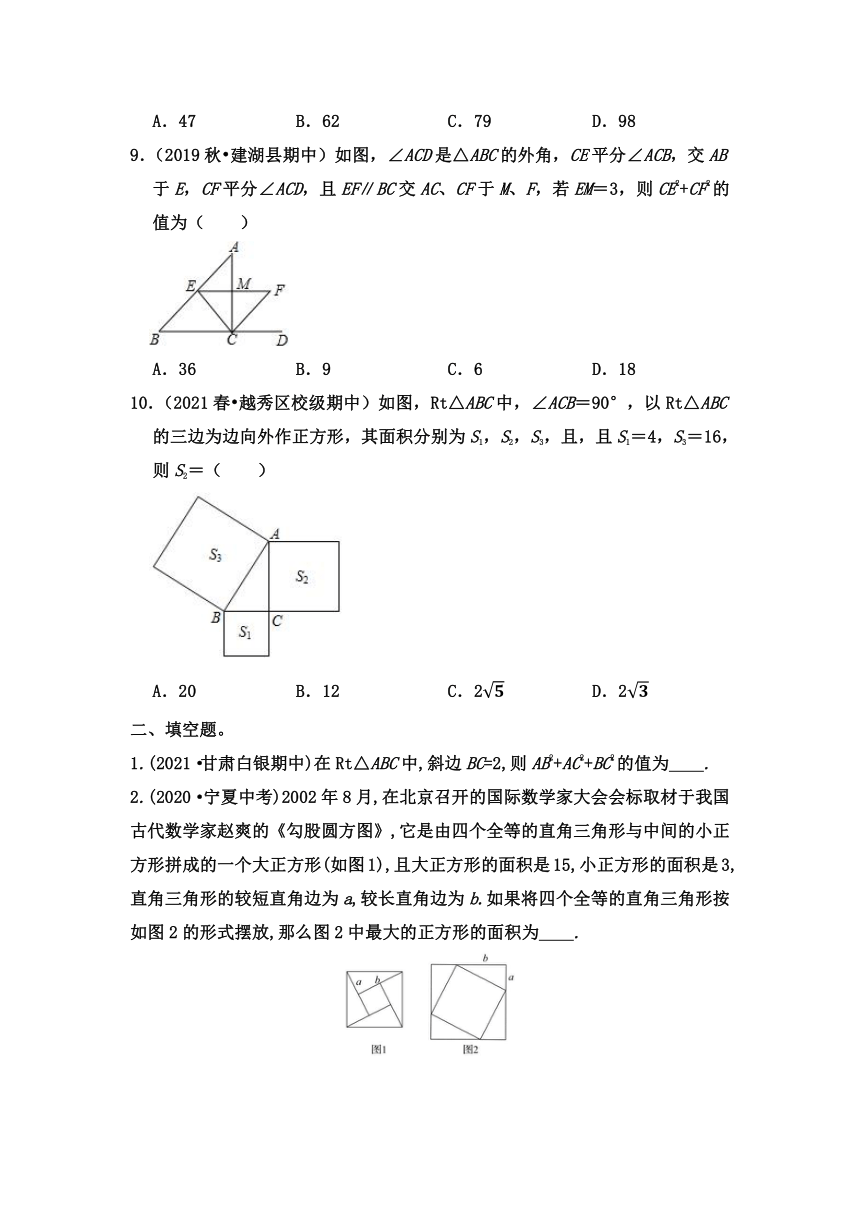
9.(2019秋 建湖县期中)如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,且EF∥BC交AC、CF于M、F,若EM=3,则CE2+CF2的值为( )
A.36 B.9 C.6 D.18
10.(2021春 越秀区校级期中)如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且,且S1=4,S3=16,则S2=( )
A.20 B.12 C.2 D.2
填空题。
1.(2021·甘肃白银期中)在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为 .
2.(2020·宁夏中考)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为 .
3.(2021·甘肃张掖质检)在Rt△ABC中,∠C=90°,周长为60,斜边与一条直角边之比为13∶5,则这个三角形的三边长分别为 .
4.在△ABC中,∠C=90°,其中a∶b=3∶4,且c=10 cm,则S△ABC= cm2.
5.(2021·内蒙古包头模拟)如图,△ABC中,AB=AC=10,BD是AC边上的高线,DC=2,则BD= .
三、解答题。
1.如下图所示,△ABC中,AB=15 cm,AC=24 cm,∠A=60°,求BC的长.
2.如下图,A、B两点都与平面镜相距4米,且A、B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点.求B点到入射点的距离.
3.如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m于点D.
试说明:EC=BD;
4.如图,一辆小汽车在一条限速为70 km/h的公路上直线行驶,某一时刻刚好行驶到路对面车速检测仪A正前方30 m的B处,过了2 s后,测得小汽车(位于C处)与车速检测仪A的距离为50 m,这辆小汽车超速了吗?
5.铁路上A,B两站(视为直线上两点)相距25 km,C,D为两个村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B.已知CA=15 km,DB=10 km.现要在A,B之间建一个土特产收购站E,使得C,D两村庄到E站的距离相等,E站应建在距离A站多远处?
答案
一、选择题。
1. C 2.A 3. C 4.D 5.A 6.B 7.D 8.C 9.A 10.B
二、填空题。
1. 8
2. 27
3. 26,10,24
4. 24
5. 6
三、解答题。
1.解:过点C作CD⊥AB于点D
在Rt△ACD中,∠A=60°
∠ACD=90°-60°=30°
AD=AC=12(cm)
CD2=AC2-AD2=242-122=432,
DB=AB-AD=15-12=3.
在Rt△BCD中,
BC2=DB2+CD2=32+432=441
BC=21 cm.
2.解:作出B点关于CD的对称点B′,连结AB′,交CD于点O,则O点就是光的入射点.
因为B′D=DB.
所以B′D=AC.
∠B′DO=∠OCA=90°,
∠B′=∠CAO
所以△B′DO≌△ACO(SSS)
则OC=OD=AB=×6=3米.
连结OB,在Rt△ODB中,OD2+BD2=OB2
所以OB2=32+42=52,即OB=5(米).
所以点B到入射点的距离为5米.
3.解:∵AE⊥m,BD⊥m,∴∠AEC=∠CDB=90°,
∵△ABC是等腰直角三角形,∴∠ACB=90°,AC=BC,
∴∠ACE+∠BCD=90°,∵∠ACE+∠CAE=90°,
∴∠CAE=∠BCD,在△AEC与△BCD中,,
∴△CAE≌△BCD(AAS),∴EC=BD.
4.解:
在Rt△ABC中,由勾股定理得,BC2=AC2-AB2=502-302=402.
所以BC=40 m,v=40÷2=20(m/s),
因为20 m/s=72 km/h,72>70,
所以这辆小汽车超速了.
5.解:设AE=x km,则BE=(25-x)km.
在Rt△ACE中,CE2=AC2+AE2=152+x2.
在Rt△BDE中,DE2=BD2+BE2=102+(25-x)2.
因为CE=DE,所以CE2=DE2,
所以152+x2=102+(25-x)2,解得x=10,
所以E站应建在距A站10 km处.
1.2 探索勾股定理
一、选择题。
1.利用四个全等的直角三角形可以拼成如图所示的图形.通过该图形,可以验证公式( )
A.(a+b)(a-b)=a2-b2
B.(a+b)2=a2+2ab+b2
C.c2=a2+b2
D.(a-b)2=a2-2ab+b2
2.(2021·新疆乌鲁木齐模拟)直角三角形中,一条直角边长为24 cm,斜边长为25 cm,则另一直角边长为 ( )
A.7 cm B.12 cm C.16 cm D.49 cm
3.如图,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA,BC为半径的两个圆形成一圆环.该圆环的面积为( )
A.π B.3π C.9π D.6π
4.如图,韩彬同学从位于超市南偏西30°的家(记作A)出发行走了4 000 m到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3 000 m到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
A.2 000 m B.3 000 m C.4 000 m D.5 000 m
5.(2021·甘肃张掖期中)如图,在由边长为1个单位长度的小正方形组成的网格中,点A, B都是格点,则线段AB的长为 ( )
A.5 B. 6 C.7 D.2
6.(2021·宁夏银川期中)若直角三角形的两直角边长分别为5 cm,12 cm,则斜边上的高为 ( )
A. cm B. cm C.13 cm D. cm
7.如图,公园内有一个长方形草坪,有少数人为避开直角走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了________路(假设2步为1 m)( )
A.1步 B.2步
C.3步 D.4步
8.(2019秋 昌平区期末)如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
9.(2019秋 建湖县期中)如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,且EF∥BC交AC、CF于M、F,若EM=3,则CE2+CF2的值为( )
A.36 B.9 C.6 D.18
10.(2021春 越秀区校级期中)如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且,且S1=4,S3=16,则S2=( )
A.20 B.12 C.2 D.2
填空题。
1.(2021·甘肃白银期中)在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为 .
2.(2020·宁夏中考)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为 .
3.(2021·甘肃张掖质检)在Rt△ABC中,∠C=90°,周长为60,斜边与一条直角边之比为13∶5,则这个三角形的三边长分别为 .
4.在△ABC中,∠C=90°,其中a∶b=3∶4,且c=10 cm,则S△ABC= cm2.
5.(2021·内蒙古包头模拟)如图,△ABC中,AB=AC=10,BD是AC边上的高线,DC=2,则BD= .
三、解答题。
1.如下图所示,△ABC中,AB=15 cm,AC=24 cm,∠A=60°,求BC的长.
2.如下图,A、B两点都与平面镜相距4米,且A、B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点.求B点到入射点的距离.
3.如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m于点D.
试说明:EC=BD;
4.如图,一辆小汽车在一条限速为70 km/h的公路上直线行驶,某一时刻刚好行驶到路对面车速检测仪A正前方30 m的B处,过了2 s后,测得小汽车(位于C处)与车速检测仪A的距离为50 m,这辆小汽车超速了吗?
5.铁路上A,B两站(视为直线上两点)相距25 km,C,D为两个村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B.已知CA=15 km,DB=10 km.现要在A,B之间建一个土特产收购站E,使得C,D两村庄到E站的距离相等,E站应建在距离A站多远处?
答案
一、选择题。
1. C 2.A 3. C 4.D 5.A 6.B 7.D 8.C 9.A 10.B
二、填空题。
1. 8
2. 27
3. 26,10,24
4. 24
5. 6
三、解答题。
1.解:过点C作CD⊥AB于点D
在Rt△ACD中,∠A=60°
∠ACD=90°-60°=30°
AD=AC=12(cm)
CD2=AC2-AD2=242-122=432,
DB=AB-AD=15-12=3.
在Rt△BCD中,
BC2=DB2+CD2=32+432=441
BC=21 cm.
2.解:作出B点关于CD的对称点B′,连结AB′,交CD于点O,则O点就是光的入射点.
因为B′D=DB.
所以B′D=AC.
∠B′DO=∠OCA=90°,
∠B′=∠CAO
所以△B′DO≌△ACO(SSS)
则OC=OD=AB=×6=3米.
连结OB,在Rt△ODB中,OD2+BD2=OB2
所以OB2=32+42=52,即OB=5(米).
所以点B到入射点的距离为5米.
3.解:∵AE⊥m,BD⊥m,∴∠AEC=∠CDB=90°,
∵△ABC是等腰直角三角形,∴∠ACB=90°,AC=BC,
∴∠ACE+∠BCD=90°,∵∠ACE+∠CAE=90°,
∴∠CAE=∠BCD,在△AEC与△BCD中,,
∴△CAE≌△BCD(AAS),∴EC=BD.
4.解:
在Rt△ABC中,由勾股定理得,BC2=AC2-AB2=502-302=402.
所以BC=40 m,v=40÷2=20(m/s),
因为20 m/s=72 km/h,72>70,
所以这辆小汽车超速了.
5.解:设AE=x km,则BE=(25-x)km.
在Rt△ACE中,CE2=AC2+AE2=152+x2.
在Rt△BDE中,DE2=BD2+BE2=102+(25-x)2.
因为CE=DE,所以CE2=DE2,
所以152+x2=102+(25-x)2,解得x=10,
所以E站应建在距A站10 km处.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
