12.1全等三角形 同步练习(含答案) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 12.1全等三角形 同步练习(含答案) 2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 110.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 00:00:00 | ||
图片预览

文档简介
12.1全等三角形 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.若 ,且 , , ,则 的长为( )
A.6 B.8 C.9 D.10
2.如图是两个全等三角形,图中的字母表示三角形的边长,则的度数是( )
A.54° B.56° C.60° D.66°
3.如图,已知 ,下列结论中错误的是( )
A. B.
C. D.
4.下列给出四个命题:
(1)面积相等的两个三角形是全等三角形(2)三个内角对应相等的两个三角形是全等三角形
(3)全等三角形的周长一定相等(4)全等三角形对应边上的高相等
正确的个数有( )
A.0个 B.1个 C.2个 D.3个
5.如图,△ABC≌△DEF,BC=12,EC=7,则CF的长为( )
A.5 B.6 C.7 D.8
6.如图,已知△AOC≌△BOD,∠A=30°,∠C=20°,则∠COD=( )
A.50° B.80° C.100° D.130°
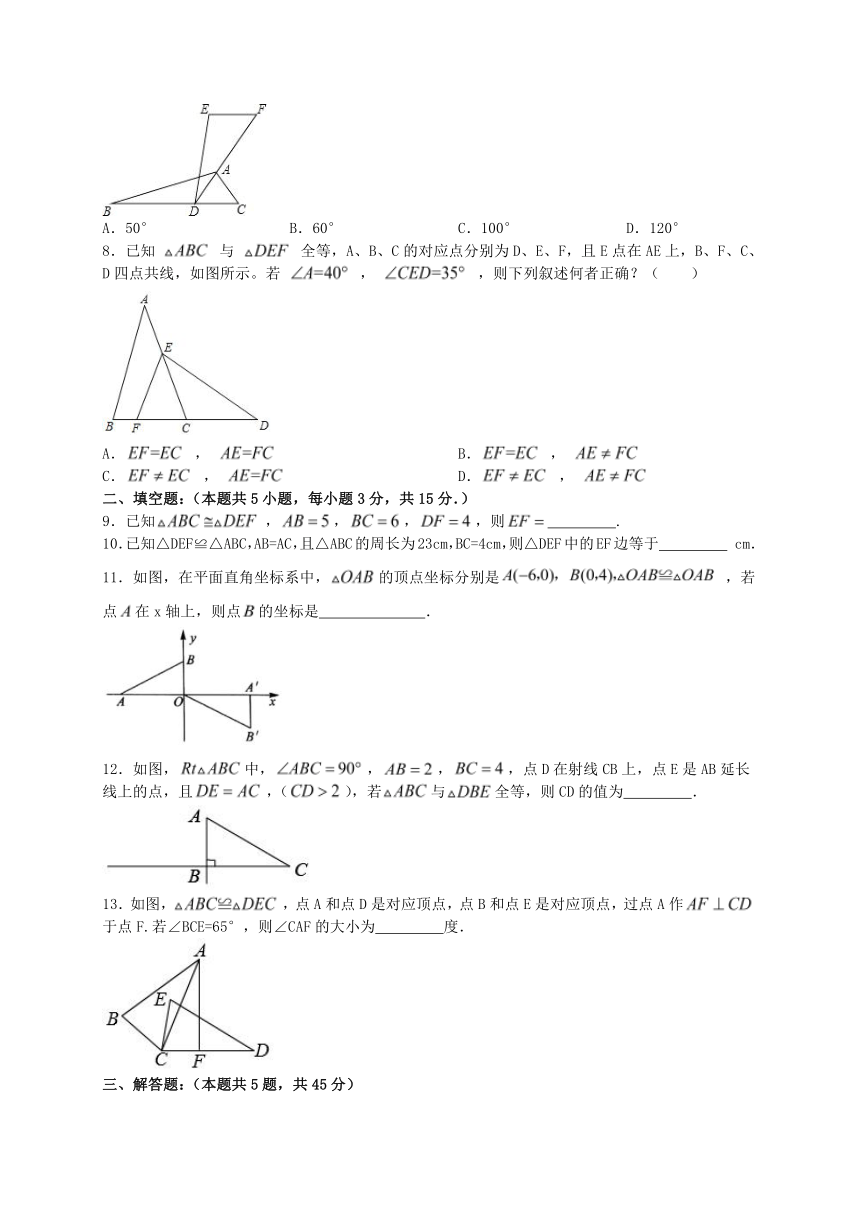
7.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
A.50° B.60° C.100° D.120°
8.已知 与 全等,A、B、C的对应点分别为D、E、F,且E点在AE上,B、F、C、D四点共线,如图所示。若 , ,则下列叙述何者正确?( )
A. , B. ,
C. , D. ,
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知,,,,则 .
10.已知△DEF≌△ABC,AB=AC,且△ABC的周长为23cm,BC=4cm,则△DEF中的EF边等于 cm.
11.如图,在平面直角坐标系中,的顶点坐标分别是,若点在x轴上,则点的坐标是 .
12.如图,中,,,,点D在射线CB上,点E是AB延长线上的点,且,(),若与全等,则CD的值为 .
13.如图,,点A和点D是对应顶点,点B和点E是对应顶点,过点A作于点F.若∠BCE=65°,则∠CAF的大小为 度.
三、解答题:(本题共5题,共45分)
14.如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.
15.如图,△ABC≌△ADE,AB=AD,AC=16cm,∠B=28°,∠E=95°,∠EAB=20°,求∠BAD的度数及AE的长.
16.如图,点B,F,C,E在同一条直线上,△ABC≌△DEF,点B与点E,点A与点D分别是对应点,AB=6,BC=11,BF=3,∠ACB=30°.求∠DFE的度数及DE,CE的长.
17.如图所示,已知△ACE≌△DBF,AD=8,BC=3.
(1)求AC的长.
(2)CE与BF平行吗?说明理由.
18.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
参考答案:
1.A 2.D 3.D 4.B 5.A 6.B 7.A 8.B
9.6
10.4
11.(6,-4)
12.6或8
13.25
14.解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
15.解:∵△ABC≌△ADE,
∴∠D=∠B=28°,AE=AC=16cm,
∵∠E=95°,
∴∠EAD=180°﹣28°﹣95°=57°,
∵∠EAB=20°,
∴∠BAD=∠BAE+∠EAD=20°+57°=77°
16.解:∵△ABC≌△DEF,点B与点E,点A与点D分别是对应点,
∴DE=AB=6,EF=BC=11,
∠DFE=∠ACB=30°.
∵CE=EF-CF,BF=BC-CF,EF=BC,
∴CE=BF=3
17.(1)解:∵△ACE≌△DBF,
∴AC=BD,
∴AB= (AD﹣BC)= ×(8﹣2)=2.5,
∴AC=AB+BC=2.5+3=5.5
(2)解:CE与BF平行
证明:∵△ACE≌△DBF,
∴∠ACE=∠DBF,
∴CE∥BF
18.(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.若 ,且 , , ,则 的长为( )
A.6 B.8 C.9 D.10
2.如图是两个全等三角形,图中的字母表示三角形的边长,则的度数是( )
A.54° B.56° C.60° D.66°
3.如图,已知 ,下列结论中错误的是( )
A. B.
C. D.
4.下列给出四个命题:
(1)面积相等的两个三角形是全等三角形(2)三个内角对应相等的两个三角形是全等三角形
(3)全等三角形的周长一定相等(4)全等三角形对应边上的高相等
正确的个数有( )
A.0个 B.1个 C.2个 D.3个
5.如图,△ABC≌△DEF,BC=12,EC=7,则CF的长为( )
A.5 B.6 C.7 D.8
6.如图,已知△AOC≌△BOD,∠A=30°,∠C=20°,则∠COD=( )
A.50° B.80° C.100° D.130°
7.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
A.50° B.60° C.100° D.120°
8.已知 与 全等,A、B、C的对应点分别为D、E、F,且E点在AE上,B、F、C、D四点共线,如图所示。若 , ,则下列叙述何者正确?( )
A. , B. ,
C. , D. ,
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知,,,,则 .
10.已知△DEF≌△ABC,AB=AC,且△ABC的周长为23cm,BC=4cm,则△DEF中的EF边等于 cm.
11.如图,在平面直角坐标系中,的顶点坐标分别是,若点在x轴上,则点的坐标是 .
12.如图,中,,,,点D在射线CB上,点E是AB延长线上的点,且,(),若与全等,则CD的值为 .
13.如图,,点A和点D是对应顶点,点B和点E是对应顶点,过点A作于点F.若∠BCE=65°,则∠CAF的大小为 度.
三、解答题:(本题共5题,共45分)
14.如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.
15.如图,△ABC≌△ADE,AB=AD,AC=16cm,∠B=28°,∠E=95°,∠EAB=20°,求∠BAD的度数及AE的长.
16.如图,点B,F,C,E在同一条直线上,△ABC≌△DEF,点B与点E,点A与点D分别是对应点,AB=6,BC=11,BF=3,∠ACB=30°.求∠DFE的度数及DE,CE的长.
17.如图所示,已知△ACE≌△DBF,AD=8,BC=3.
(1)求AC的长.
(2)CE与BF平行吗?说明理由.
18.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
参考答案:
1.A 2.D 3.D 4.B 5.A 6.B 7.A 8.B
9.6
10.4
11.(6,-4)
12.6或8
13.25
14.解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
15.解:∵△ABC≌△ADE,
∴∠D=∠B=28°,AE=AC=16cm,
∵∠E=95°,
∴∠EAD=180°﹣28°﹣95°=57°,
∵∠EAB=20°,
∴∠BAD=∠BAE+∠EAD=20°+57°=77°
16.解:∵△ABC≌△DEF,点B与点E,点A与点D分别是对应点,
∴DE=AB=6,EF=BC=11,
∠DFE=∠ACB=30°.
∵CE=EF-CF,BF=BC-CF,EF=BC,
∴CE=BF=3
17.(1)解:∵△ACE≌△DBF,
∴AC=BD,
∴AB= (AD﹣BC)= ×(8﹣2)=2.5,
∴AC=AB+BC=2.5+3=5.5
(2)解:CE与BF平行
证明:∵△ACE≌△DBF,
∴∠ACE=∠DBF,
∴CE∥BF
18.(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3
