第十一章三角形 章节练习(含答案) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 第十一章三角形 章节练习(含答案) 2023-2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 14:43:59 | ||
图片预览


文档简介
第十一章三角形 章节练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
A.两点之间线段最短 B.三角形的稳定性
C.垂线段最短 D.两直线平行,内错角相等
2.如果在一个顶点周围用两个正方形和n个正三角形恰好可以进行平面镶嵌,则n的值是( )
A.3 B.4 C.5 D.6
3.在△ABC中, ,则△ABC是( )
A.等腰直角三角形 B.锐角三角形
C.钝角三角形 D.直角三角形
4.如果三角形的两边长分别为3和5,则第三边L的取值范围是( )
A.25.如图,正五边形ABCDE,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G=( )
A.36° B.54° C.60° D.72°
6.如图,已知,那么的度数是( )
A.180° B.280° C.320° D.360°
7.如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )
A.65° B.66° C.70° D.78°
8.如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△BED的面积为3cm2,则△ABC的面积为( )cm2 .
A.24 B.12 C.9 D.6
二、填空题:(本题共5小题,每小题3分,共15分.)
9.一个三角形的底边a增加了k,该边上的高h减少k后,若其面积保持不变,则a-h= .
10.已知两个多边形的内角和为1800°,且这两个多边形的边数之比为,则这两个多边形的边数之和为 .
11.如图,已知直线,点A在直线a上,点B、C在直线b上,点P在线段上,如果,,那么 .
12.如图,DE⊥AB,∠A=25°,∠D=45°,则∠ACB的度数为 .
13.如图,在中,E是的中点,点D在上,且,与交于点F,若,则的面积为 .
三、解答题:(本题共5题,共45分)
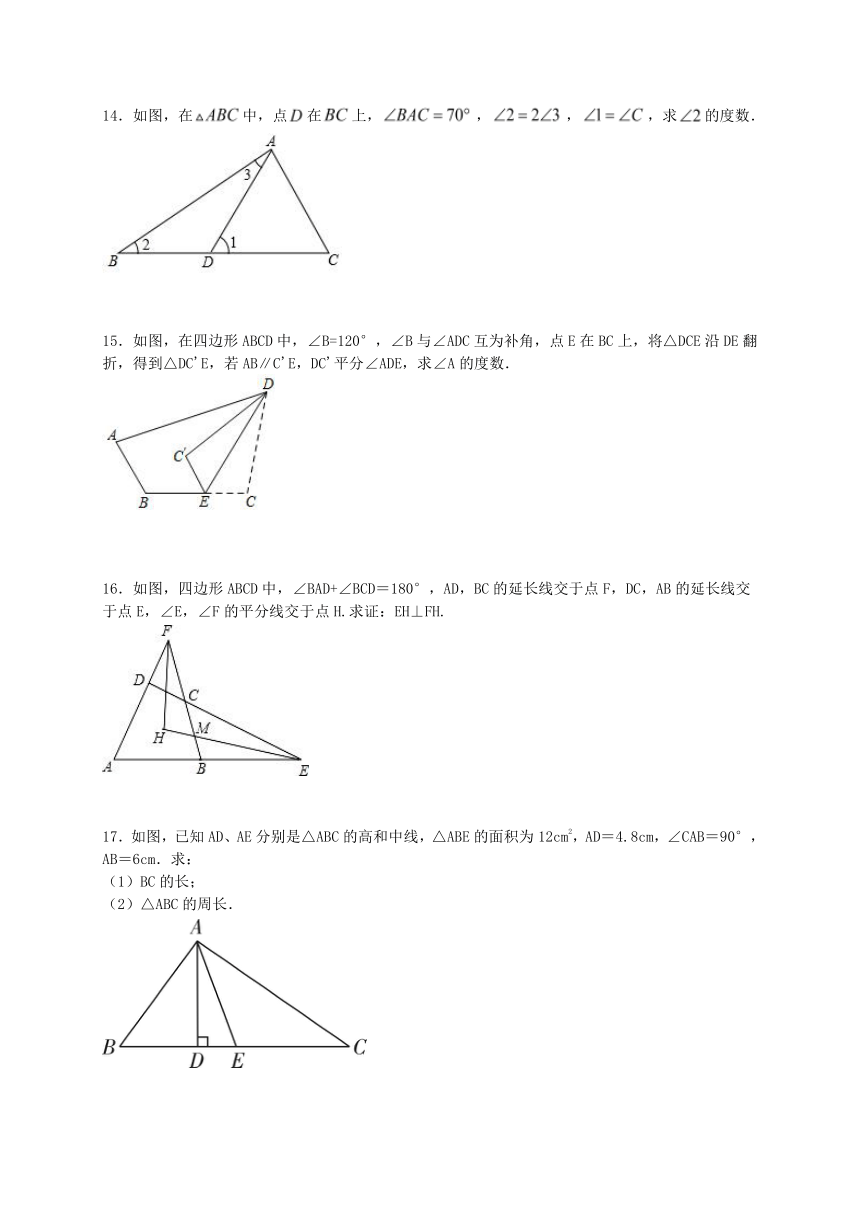
14.如图,在中,点在上,,,,求的度数.
15.如图,在四边形ABCD中,∠B=120°,∠B与∠ADC互为补角,点E在BC上,将△DCE沿DE翻折,得到△DC'E,若AB∥C'E,DC'平分∠ADE,求∠A的度数.
16.如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
17.如图,已知AD、AE分别是△ABC的高和中线,△ABE的面积为12cm2,AD=4.8cm,∠CAB=90°,AB=6cm.求:
(1)BC的长;
(2)△ABC的周长.
18.如图,在 中,点D在 上, 的平分线交 于点E,过点A作 的平行线交 于点F,交 于点 .
(1)若 , ,求 的度数;
(2)若 ,请说明 .
参考答案:
1.B 2.A 3.D 4.C 5.B 6.C 7.C 8.B
9.-k
10.14
11.
12.110°
13.12
14.解:∵ ,可设∠3=x°,则∠2=2x°
∴∠1=∠2+∠3=3x°
∵
∴∠C=3x°
∵∠BAC+∠B+∠C=180°
∴ +2x+3x=180
解得:x=22
∴∠2=44°
15.解:∵∠B=120°,∠B与∠ADC互为补角,
∴∠ADC=180°-∠B=180°-120°=60°,
由折叠的性质得:∠CDE=∠C'DE,∠CED=∠C'ED,
∵DC'平分∠ADE,
∴∠ADC'=∠C'DE,
∴∠CDE=∠ADC'=∠C'DE==20°,
∵AB∥C'E,
∴∠CEC'=∠B=120°,
∴∠CED==60°,
∴∠C=180°-∠EDC-∠DEC=180°-20°-60°=100°,
∴∠A=360°-∠B-∠C-∠ADC=80°.
16.证明:连接EF,则∠CFE+∠CEF+∠FCE=180°,
∵∠BAD+∠BCD=180°,∠FCE=∠BCD,
∴∠BAD+∠FCE=180°,
∵∠E,∠F的平分线交于点H,
∴∠CFH= ∠CFA,∠HEC= ∠BED,
在△AEF中,
∵∠A+∠CFA+∠CFE+∠CEF+∠BED=180°,
∴∠CFH+∠BEH+∠CEF+∠FCE=90°,
在△HEF中,
∠CFH+∠BEH+∠CEF+∠FCE+∠H=180°,
∴∠H=90°,
∴EH⊥FH.
17.(1)解:∵△ABE的面积为12cm2,AD是△ABC的高,AD=4.8cm,
∴=5cm,
∵AE是△ABC的中线,
∴BC=2BE=10cm;
(2)解:∵AD是△ABC的高,AD=4.8cm,BC=10cm,
∴△ABC的面积:=24cm2,
∵在△ABC中,∠CAB=90°,AB=6cm,
∴△ABC的面积:=24cm2
∴AC=8cm,
∴△ABC的周长:AC+BC+AB=24cm.
18.(1)解:∵AF∥DE,∠2=80°,
∴∠4=∠2=80°,
∵∠4=∠1+∠BDE,∠1=30°,
∴∠BDE=80°-30°=50°,
∵DE是∠BDC的平分线,
∴∠BDC=2∠BDE=100°,
∴∠C=180°-∠1-∠BDC=180°-30°-100°=50°
(2)解:由(1)得:∠4=∠2=∠1+∠5+∠3,即∠1=∠4-∠5-∠3①,
∵∠BDC=2∠ABC,即 ∠BDC=∠BDE=∠ABC=∠1+∠5,
∴∠4=∠1+∠BDE=∠1+∠1+∠5=2∠1+∠5,即∠4=2∠1+∠5②,
①代入②得:∠4=2∠4-2∠5-2∠3+∠5,
整理得:∠4=∠5+2∠3
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
A.两点之间线段最短 B.三角形的稳定性
C.垂线段最短 D.两直线平行,内错角相等
2.如果在一个顶点周围用两个正方形和n个正三角形恰好可以进行平面镶嵌,则n的值是( )
A.3 B.4 C.5 D.6
3.在△ABC中, ,则△ABC是( )
A.等腰直角三角形 B.锐角三角形
C.钝角三角形 D.直角三角形
4.如果三角形的两边长分别为3和5,则第三边L的取值范围是( )
A.2
A.36° B.54° C.60° D.72°
6.如图,已知,那么的度数是( )
A.180° B.280° C.320° D.360°
7.如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )
A.65° B.66° C.70° D.78°
8.如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△BED的面积为3cm2,则△ABC的面积为( )cm2 .
A.24 B.12 C.9 D.6
二、填空题:(本题共5小题,每小题3分,共15分.)
9.一个三角形的底边a增加了k,该边上的高h减少k后,若其面积保持不变,则a-h= .
10.已知两个多边形的内角和为1800°,且这两个多边形的边数之比为,则这两个多边形的边数之和为 .
11.如图,已知直线,点A在直线a上,点B、C在直线b上,点P在线段上,如果,,那么 .
12.如图,DE⊥AB,∠A=25°,∠D=45°,则∠ACB的度数为 .
13.如图,在中,E是的中点,点D在上,且,与交于点F,若,则的面积为 .
三、解答题:(本题共5题,共45分)
14.如图,在中,点在上,,,,求的度数.
15.如图,在四边形ABCD中,∠B=120°,∠B与∠ADC互为补角,点E在BC上,将△DCE沿DE翻折,得到△DC'E,若AB∥C'E,DC'平分∠ADE,求∠A的度数.
16.如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
17.如图,已知AD、AE分别是△ABC的高和中线,△ABE的面积为12cm2,AD=4.8cm,∠CAB=90°,AB=6cm.求:
(1)BC的长;
(2)△ABC的周长.
18.如图,在 中,点D在 上, 的平分线交 于点E,过点A作 的平行线交 于点F,交 于点 .
(1)若 , ,求 的度数;
(2)若 ,请说明 .
参考答案:
1.B 2.A 3.D 4.C 5.B 6.C 7.C 8.B
9.-k
10.14
11.
12.110°
13.12
14.解:∵ ,可设∠3=x°,则∠2=2x°
∴∠1=∠2+∠3=3x°
∵
∴∠C=3x°
∵∠BAC+∠B+∠C=180°
∴ +2x+3x=180
解得:x=22
∴∠2=44°
15.解:∵∠B=120°,∠B与∠ADC互为补角,
∴∠ADC=180°-∠B=180°-120°=60°,
由折叠的性质得:∠CDE=∠C'DE,∠CED=∠C'ED,
∵DC'平分∠ADE,
∴∠ADC'=∠C'DE,
∴∠CDE=∠ADC'=∠C'DE==20°,
∵AB∥C'E,
∴∠CEC'=∠B=120°,
∴∠CED==60°,
∴∠C=180°-∠EDC-∠DEC=180°-20°-60°=100°,
∴∠A=360°-∠B-∠C-∠ADC=80°.
16.证明:连接EF,则∠CFE+∠CEF+∠FCE=180°,
∵∠BAD+∠BCD=180°,∠FCE=∠BCD,
∴∠BAD+∠FCE=180°,
∵∠E,∠F的平分线交于点H,
∴∠CFH= ∠CFA,∠HEC= ∠BED,
在△AEF中,
∵∠A+∠CFA+∠CFE+∠CEF+∠BED=180°,
∴∠CFH+∠BEH+∠CEF+∠FCE=90°,
在△HEF中,
∠CFH+∠BEH+∠CEF+∠FCE+∠H=180°,
∴∠H=90°,
∴EH⊥FH.
17.(1)解:∵△ABE的面积为12cm2,AD是△ABC的高,AD=4.8cm,
∴=5cm,
∵AE是△ABC的中线,
∴BC=2BE=10cm;
(2)解:∵AD是△ABC的高,AD=4.8cm,BC=10cm,
∴△ABC的面积:=24cm2,
∵在△ABC中,∠CAB=90°,AB=6cm,
∴△ABC的面积:=24cm2
∴AC=8cm,
∴△ABC的周长:AC+BC+AB=24cm.
18.(1)解:∵AF∥DE,∠2=80°,
∴∠4=∠2=80°,
∵∠4=∠1+∠BDE,∠1=30°,
∴∠BDE=80°-30°=50°,
∵DE是∠BDC的平分线,
∴∠BDC=2∠BDE=100°,
∴∠C=180°-∠1-∠BDC=180°-30°-100°=50°
(2)解:由(1)得:∠4=∠2=∠1+∠5+∠3,即∠1=∠4-∠5-∠3①,
∵∠BDC=2∠ABC,即 ∠BDC=∠BDE=∠ABC=∠1+∠5,
∴∠4=∠1+∠BDE=∠1+∠1+∠5=2∠1+∠5,即∠4=2∠1+∠5②,
①代入②得:∠4=2∠4-2∠5-2∠3+∠5,
整理得:∠4=∠5+2∠3
