人教版数学八年级上册 13.2画轴对称图形[1]课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.2画轴对称图形[1]课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 737.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-02 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
13.2 画轴对称图形
新课导入
P
P
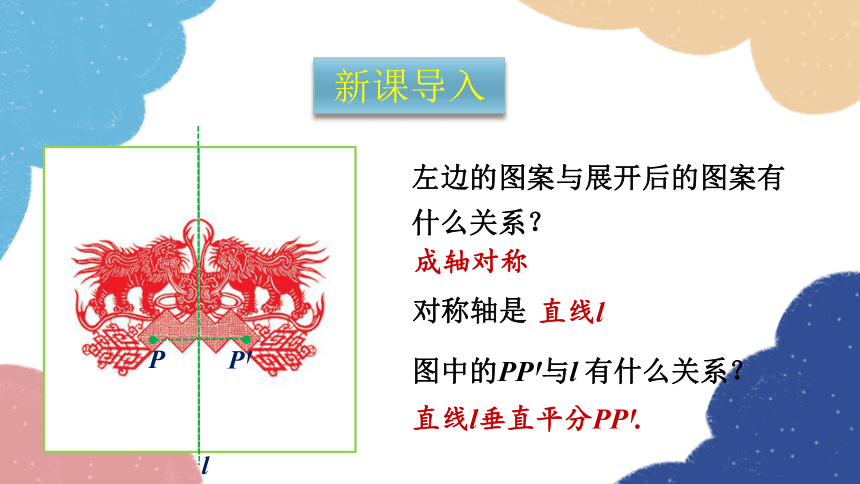
左边的图案与展开后的图案有什么关系?
成轴对称
对称轴是
直线l
图中的PP 与l 有什么关系?
l
直线l垂直平分PP .
归纳1:轴对称变换的特征
问题:如何画出几何图形关于某条直线对称的图形呢?
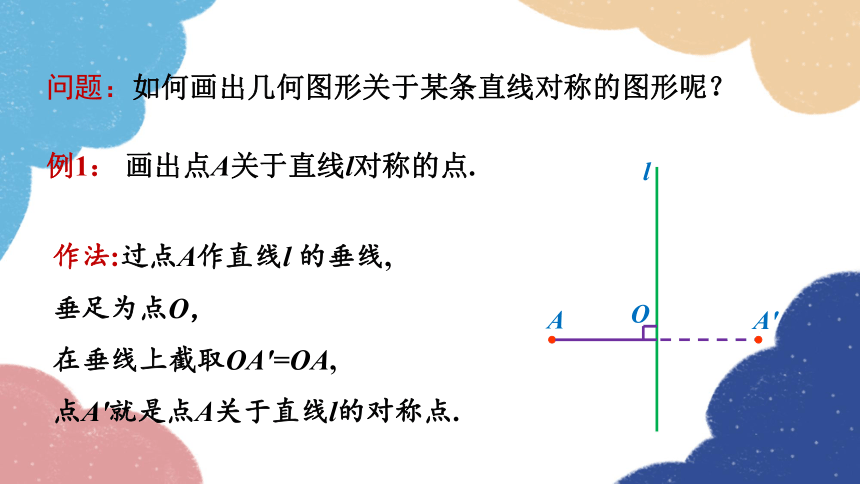
例1: 画出点A关于直线l对称的点.
A
A′
O
l
作法:过点A作直线l 的垂线,
垂足为点O,
在垂线上截取OA′=OA,
点A′就是点A关于直线l的对称点.
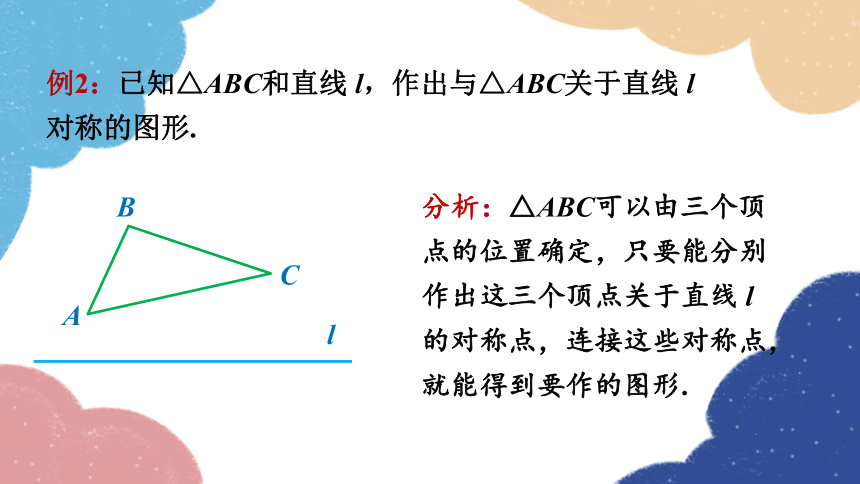
例2:已知△ABC和直线 l,作出与△ABC关于直线 l 对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线 l 的对称点,连接这些对称点,就能得到要作的图形.
B
A
C
l
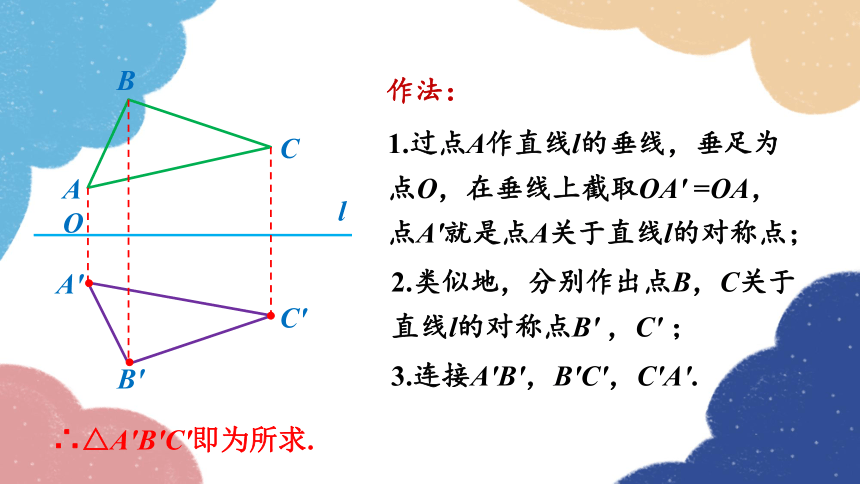
1.过点A作直线l的垂线,垂足为点O,在垂线上截取OA′ =OA,点A′就是点A关于直线l的对称点;
作法:
2.类似地,分别作出点B,C关于直线l的对称点B′ ,C′ ;
3.连接A′B′,B′C′,C′A′.
B
A
C
l
A′
B′
C′
O
∴△A′B′C′即为所求.
1.几何图形都可以看作由点组成.
2.对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
归纳2:几何图形关于某条直线对称的图形
利用坐标系画轴对称图形
1.在平面直角坐标系中画出点关于 x 轴的对称点.
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
已知点 关于 x 轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A′( 2,3)
B′( -1,-2)
C′( -6,5)
E′( 4,0)
D′( ,-1)
点(a, b)关于x轴对称的点的坐标为_________.
(a,-b)
关于x轴对称的点横坐标相等,纵坐标互为相反数.
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
已知点 关于 x 轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A′( 2,3)
B′( -1,-2)
C′( -6,5)
E′( 4,0)
D′( ,-1)
你有什么发现?
2.在平面直角坐标系中画出点关于y轴的对称点.
x
y
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
已知点 关于x轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A〞(-2,-3)
B〞(1,2)
C〞( 6,-5)
E〞( -4,0)
D〞(- ,1)
关于y轴对称的点纵坐标相等,横坐标互为相反数.
点(a, b)关于y轴对称的点的坐标为_________.
(-a,b)
x
y
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
已知点 关于x轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A〞(-2,-3)
B〞(1,2)
C〞( 6,-5)
E〞( -4,0)
D〞(- ,1)
你有什么发现?
归纳3:关于坐标轴对称的点的特征
例3:作出与△ABC关于y轴对称的图形.
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
A
解:点A(-4,1) 、B(-3,2)、C(-1,-1)关于y轴对称的
点的坐标分别是A′(4, 1)
B′ (3, 2),C′ (1,-1).
B
C
A′
B′
C′
△A′B′ C′即为所求图形.
变式练习:作出与△ABC关于x轴对称的图形.
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
A
解:点A(-4,1) 、B(-3,2)、C(-1,-1)关于x轴对称的
点的坐标分别是A′(-4, -1)
B′ (-3, -2),C′ (-1, 1).
B
C
A′
B′
C′
△A′B′ C′即为所求图形.
画某图形关于x轴或关于y轴的对称图形,
只要画出图形中的一些特殊点关于x轴或关于y轴的的对称点,
连接这些对称点,就可以得到原图形的轴对称图形.
归纳4:画一个图形关于x 轴或y 轴对称的图形的方法
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
随堂练习
1.完成下表.
已知点 (3,-3) (-1,2) (8,-5) (0,-1)
关于x轴的对称点
关于y轴的对称点
(-3, -3)
(3,3)
(-1,-2)
(1, 2)
(-8, -5)
(8, 5)
(0, -1)
(0,1)
2.在如图所示编号为①②③④的四个三角形中,关于 y 轴对称的两个三角形的编号为 ;关于x轴对称的两个三角形的编号为 .
y
x
-1
-2
-4
-3
-1
-2
-4
-3
1
2
4
3
1
2
4
3
O
①
②
③
④
①与②
②与③
3.已知点P(2a+b,-3a)与点P'(8,b+2).
若点P与点P'关于x轴对称,则a=_____ ,b=_______.
若点P与点P'关于y轴对称,则a=_____ ,b=_______.
6
-20
2
4
13.2 画轴对称图形
新课导入
P
P
左边的图案与展开后的图案有什么关系?
成轴对称
对称轴是
直线l
图中的PP 与l 有什么关系?
l
直线l垂直平分PP .
归纳1:轴对称变换的特征
问题:如何画出几何图形关于某条直线对称的图形呢?
例1: 画出点A关于直线l对称的点.
A
A′
O
l
作法:过点A作直线l 的垂线,
垂足为点O,
在垂线上截取OA′=OA,
点A′就是点A关于直线l的对称点.
例2:已知△ABC和直线 l,作出与△ABC关于直线 l 对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别作出这三个顶点关于直线 l 的对称点,连接这些对称点,就能得到要作的图形.
B
A
C
l
1.过点A作直线l的垂线,垂足为点O,在垂线上截取OA′ =OA,点A′就是点A关于直线l的对称点;
作法:
2.类似地,分别作出点B,C关于直线l的对称点B′ ,C′ ;
3.连接A′B′,B′C′,C′A′.
B
A
C
l
A′
B′
C′
O
∴△A′B′C′即为所求.
1.几何图形都可以看作由点组成.
2.对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
归纳2:几何图形关于某条直线对称的图形
利用坐标系画轴对称图形
1.在平面直角坐标系中画出点关于 x 轴的对称点.
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
已知点 关于 x 轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A′( 2,3)
B′( -1,-2)
C′( -6,5)
E′( 4,0)
D′( ,-1)
点(a, b)关于x轴对称的点的坐标为_________.
(a,-b)
关于x轴对称的点横坐标相等,纵坐标互为相反数.
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
已知点 关于 x 轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A′( 2,3)
B′( -1,-2)
C′( -6,5)
E′( 4,0)
D′( ,-1)
你有什么发现?
2.在平面直角坐标系中画出点关于y轴的对称点.
x
y
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
已知点 关于x轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A〞(-2,-3)
B〞(1,2)
C〞( 6,-5)
E〞( -4,0)
D〞(- ,1)
关于y轴对称的点纵坐标相等,横坐标互为相反数.
点(a, b)关于y轴对称的点的坐标为_________.
(-a,b)
x
y
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
已知点 关于x轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
D( ,1)
E(4,0)
A〞(-2,-3)
B〞(1,2)
C〞( 6,-5)
E〞( -4,0)
D〞(- ,1)
你有什么发现?
归纳3:关于坐标轴对称的点的特征
例3:作出与△ABC关于y轴对称的图形.
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
A
解:点A(-4,1) 、B(-3,2)、C(-1,-1)关于y轴对称的
点的坐标分别是A′(4, 1)
B′ (3, 2),C′ (1,-1).
B
C
A′
B′
C′
△A′B′ C′即为所求图形.
变式练习:作出与△ABC关于x轴对称的图形.
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
A
解:点A(-4,1) 、B(-3,2)、C(-1,-1)关于x轴对称的
点的坐标分别是A′(-4, -1)
B′ (-3, -2),C′ (-1, 1).
B
C
A′
B′
C′
△A′B′ C′即为所求图形.
画某图形关于x轴或关于y轴的对称图形,
只要画出图形中的一些特殊点关于x轴或关于y轴的的对称点,
连接这些对称点,就可以得到原图形的轴对称图形.
归纳4:画一个图形关于x 轴或y 轴对称的图形的方法
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线.
随堂练习
1.完成下表.
已知点 (3,-3) (-1,2) (8,-5) (0,-1)
关于x轴的对称点
关于y轴的对称点
(-3, -3)
(3,3)
(-1,-2)
(1, 2)
(-8, -5)
(8, 5)
(0, -1)
(0,1)
2.在如图所示编号为①②③④的四个三角形中,关于 y 轴对称的两个三角形的编号为 ;关于x轴对称的两个三角形的编号为 .
y
x
-1
-2
-4
-3
-1
-2
-4
-3
1
2
4
3
1
2
4
3
O
①
②
③
④
①与②
②与③
3.已知点P(2a+b,-3a)与点P'(8,b+2).
若点P与点P'关于x轴对称,则a=_____ ,b=_______.
若点P与点P'关于y轴对称,则a=_____ ,b=_______.
6
-20
2
4
