正多边形和圆

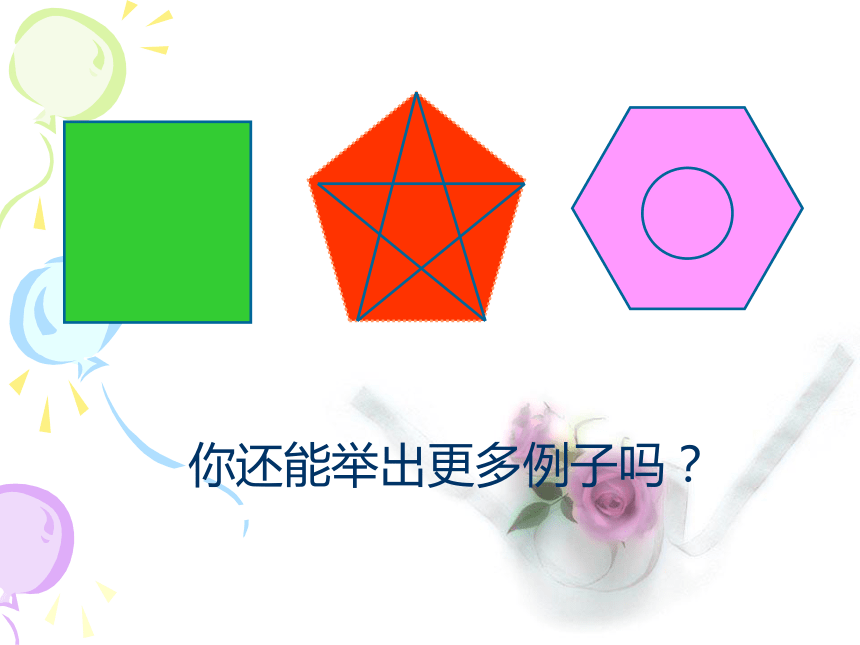
课件22张PPT。你还能举出更多例子吗？正多边形和圆圆的内接正n边形&圆的外切正n边形正多边形：
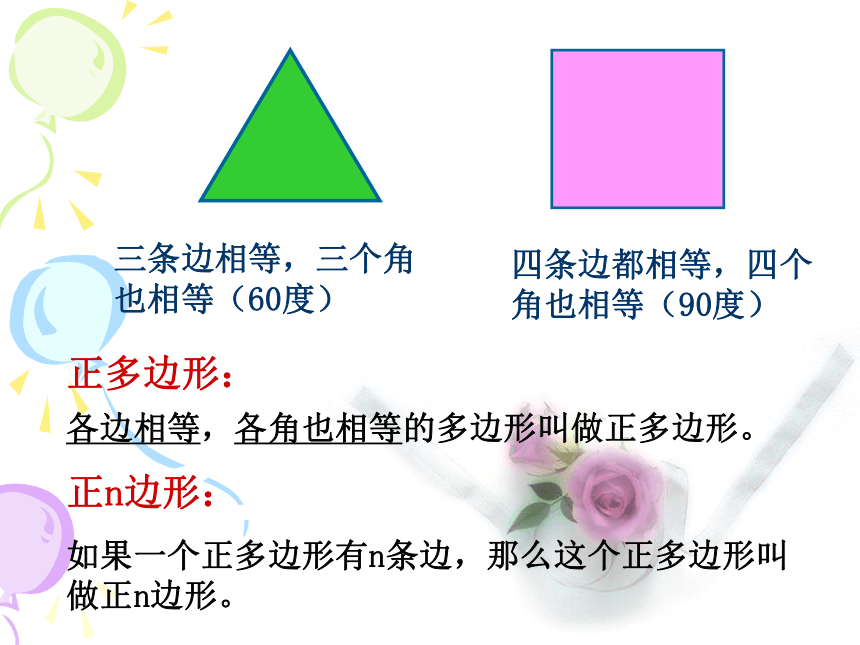
各边相等，各角也相等的多边形叫做正多边形。
正n边形：
如果一个正多边形有n条边，那么这个正多边形叫做正n边形。三条边相等，三个角也相等（60度）四条边都相等，四个角也相等（90度）想一想：
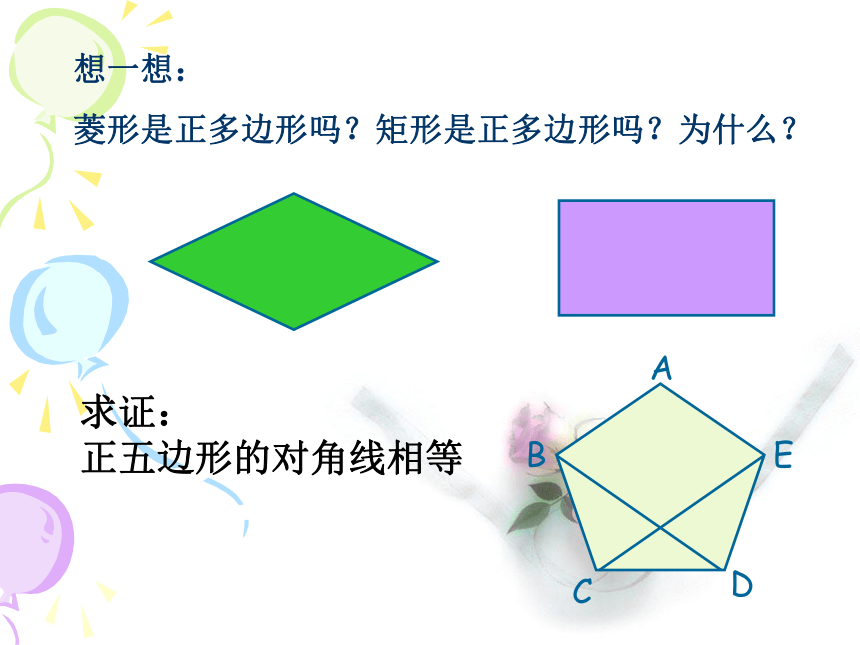
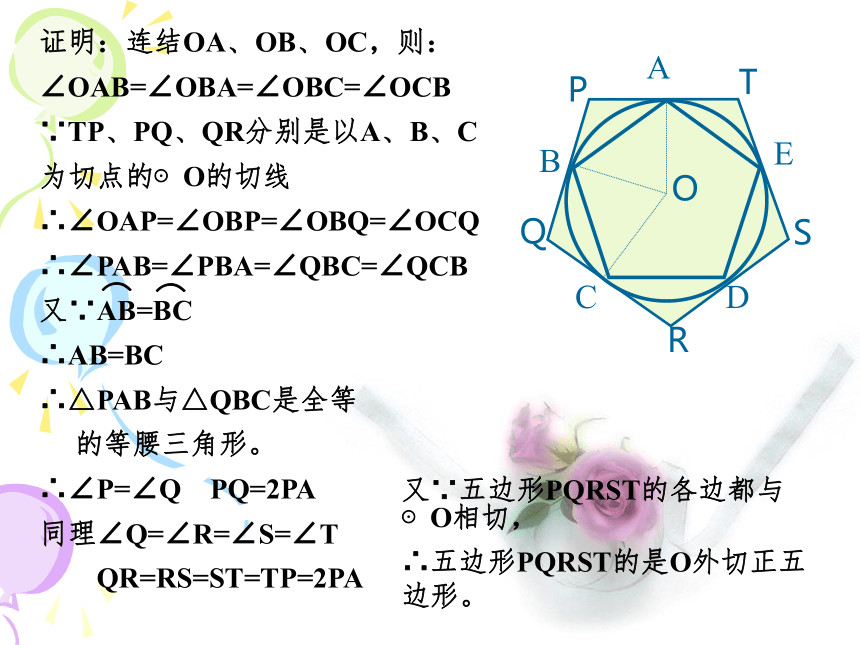
菱形是正多边形吗？矩形是正多边形吗？为什么？求证：正五边形的对角线相等类比联想怎样找圆的内接正三角形？怎样找圆的外切正三角形？怎样找圆的内接正方形？怎样找圆的外切正方形？
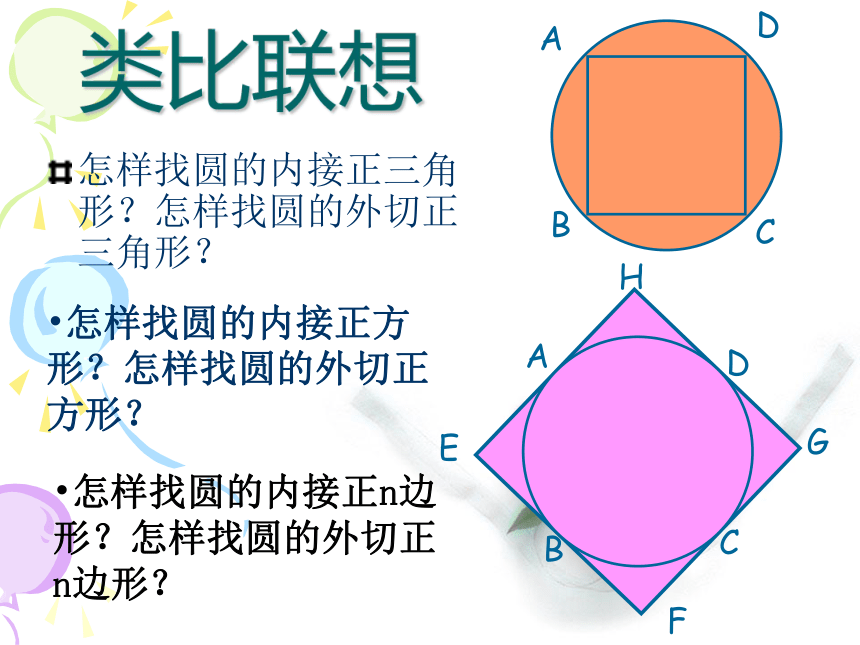
怎样找圆的内接正n边形？怎样找圆的外切正n边形？把圆分成n（n≥3）等份：
⑴依次连结各分点所得的多边形是这个圆的内接正多边形；
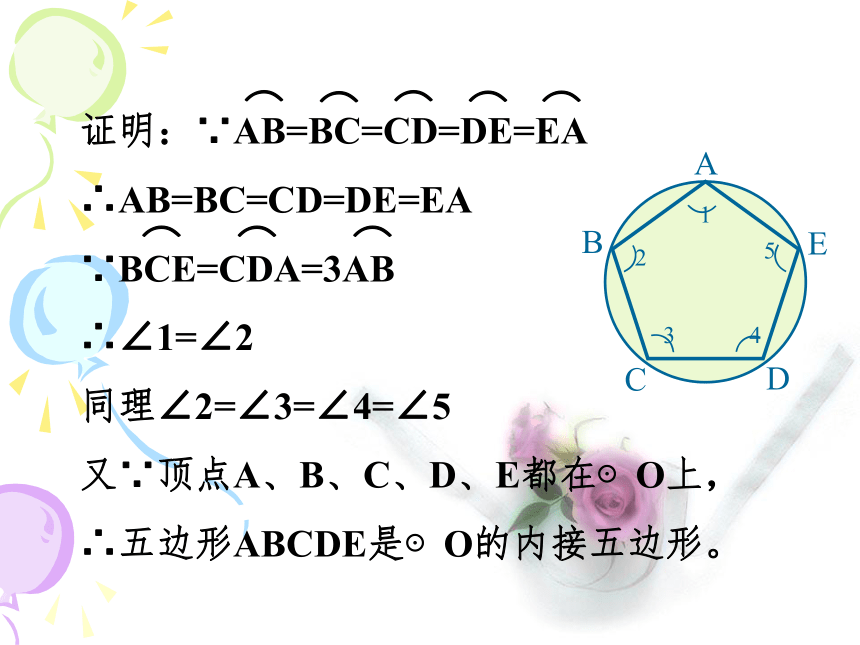
⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正多边形。定理证明：∵AB=BC=CD=DE=EA
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
∴∠1=∠2
同理∠2=∠3=∠4=∠5
又∵顶点A、B、C、D、E都在⊙O上，
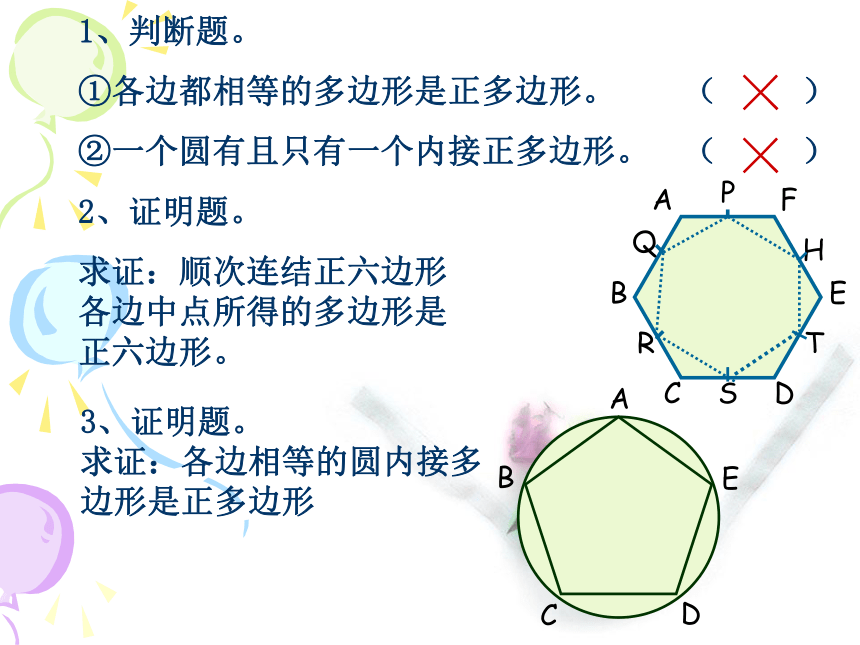
∴五边形ABCDE是⊙O的内接五边形。⌒⌒⌒⌒⌒⌒⌒⌒1、判断题。
①各边都相等的多边形是正多边形。 （ ）
②一个圆有且只有一个内接正多边形。 （ ）
2、证明题。
求证：顺次连结正六边形各边中点所得的多边形是正六边形。××3、证明题。求证：各边相等的圆内接多边形是正多边形正多边形和圆正n边形的外接圆&正n边形的内切圆定理把圆分成n（n≥3）等份：
依次连结各分点所得的多边形是这个圆的内接正n边形；
经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形。一个正多边形是否一定有外接圆和内切圆？类比联想正三角形
有没有外接圆和内切圆？
怎样作出这两个圆？
这两个圆有什么位置关系？正方形
有没有外接圆和内切圆？
怎样作出这两个圆？
这两个圆有什么位置关系？那么，正n边形呢？定理任何正多边形都有一个外接圆和一个内切圆，并且这两个圆是同心圆。正多边形的外接圆（或内切圆）的圆心叫做正多边形的中心，外接圆的半径叫做正多边形的半径，内切圆的半径叫做正多边形的边心距。正多边形各边所对的外接圆的圆心角叫做正多边形的中心角。正n边形的每个中心角都等于360°/n。正多边形的性质正多边形是轴对称图形，正n边形有n条对称轴。
若n为偶数，则其为中心对称图形。正多边形和圆巩固练习正多边形的性质各边相等，各角相等
圆的内接正n边形的各个顶点把圆分成n等分
圆的外切正n边形的各边与圆的n个切点把圆分成n等分
每个正多边形都有一个内切圆和外接圆，这两个圆是同心圆，圆心就是正多边形的中心
正多边形都是轴对称图形，如果边数是偶数那么它还是中心对称图形
正n边形的中心角和它的每个外角都等于360°/n，每个内角都等于(n-2)·180°/n
边数相同的正多边形相似，周长比、边长比、半径比、边心距比、对应对角线比都等于相似比，面积比等于相似比平方求证：各边相等的圆内接多边形是正多边形。求证：各角相等的圆外切多边形是正多边形。思考：
各边相等的圆外切多边形是否是正多边形？
各角相等的圆内接多边形是否是正多边形？练习1、下列图形中：①正五边形；②等腰三角形；③正八边形；④正2n（n为自然数）边形；⑤任意的平行四边形。是轴对称图形的有__________,是中心对称图形的有________,既是中心对称图形，又是轴对称图形的有_______。①②③④③④⑤③④2、两个正七边形的边心距之比为3:4，则它们的边长比为_____，面积比为_____，外接圆周长比是______，中心角度数比是______。3:49:163:41:1边数相同的两个正多边形相似3、已知正三角形ABC的边长为4，则它的内切圆和外接圆组成的圆环面积是多少？练习练习4、圆内接正五边形ABCDE中，对角线AC和BE相交于点M，(1)求∠AME的度数(2)求证：ME=AB(3)求证：ME2=BE·BM5、如图，AD是⊙O的直径，弦BC垂直平分OD，垂足为M。求证：△ABC是正三角形。由此你想到了尺规作图中作正三角形的方法了吗？6、A、B、C在⊙O上，且B在弧AC上，AB、AC分别是正九边形和正六边形的一边。请问：BC是此圆内接正几边形的一边？