11.1.2 三角形的高、中线与角平分线 课时检测(无答案)2023-2024学年人教版八年级数学 上册
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线 课时检测(无答案)2023-2024学年人教版八年级数学 上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 00:00:00 | ||
图片预览


文档简介
第十一章 三角形
11.1.2 三角形的高、中线与角平分线
班级______ 姓名_______ 学号_____
一、选择题
1.下列说法错误的是( )
A.三角形的三条高的交点一定在三角形内部
B.三角形的三条中线的交点一定在三角形内部
C.三角形的三条角平分线的交点一定在三角形内部
D.三角形的高,中线和角平分线都有三条
2.在中,是的中线.看到图形,甲、乙、丙、丁四名同学给出四个不同的结论,其中正确的是( )
甲:
乙:
丙:
丁:
A.甲 B.乙 C.丙 D.丁
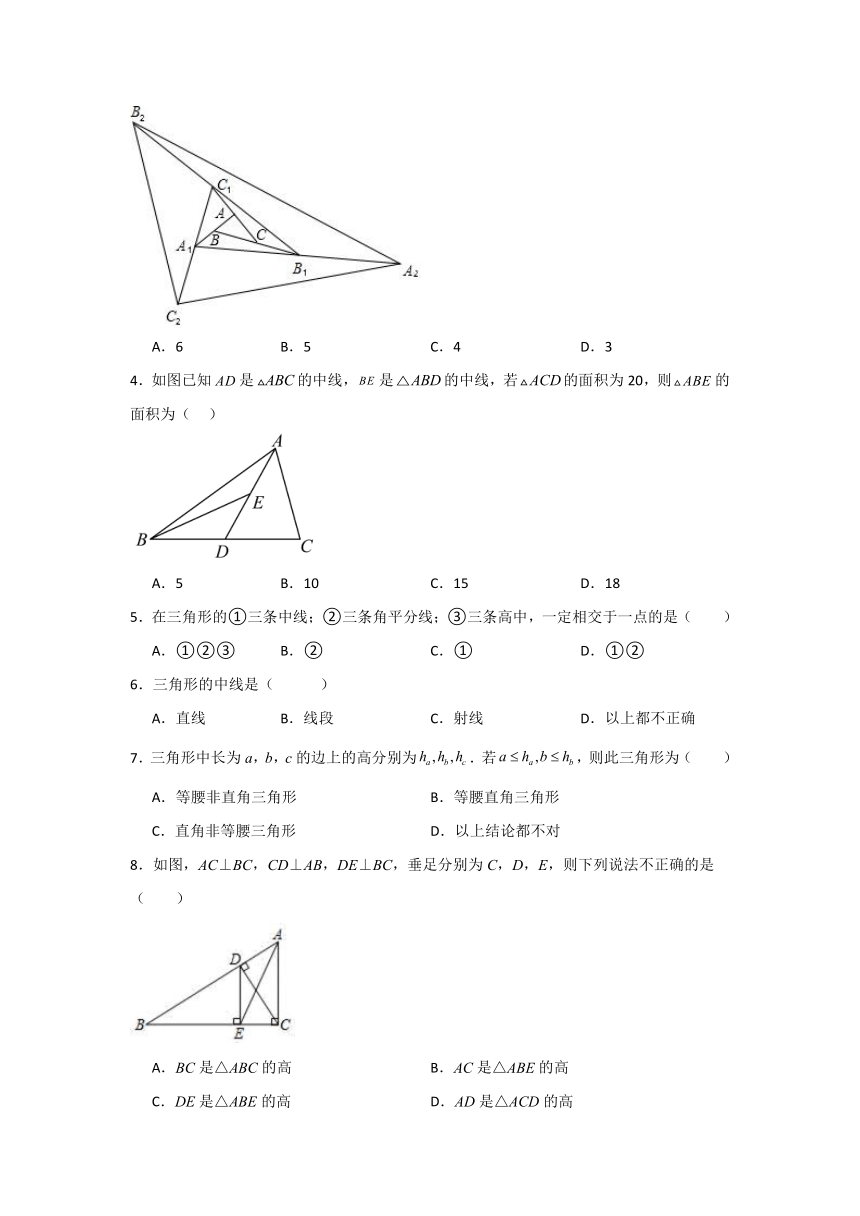
3.如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,第n次操作后,得到△AnBnCn,要使△AnBnCn的面积超过2021,则至少需要操作( )次.
A.6 B.5 C.4 D.3
4.如图已知是的中线,是的中线,若的面积为20,则的面积为( )
A.5 B.10 C.15 D.18
5.在三角形的①三条中线;②三条角平分线;③三条高中,一定相交于一点的是( )
A.①②③ B.② C.① D.①②
6.三角形的中线是( )
A.直线 B.线段 C.射线 D.以上都不正确
7.三角形中长为a,b,c的边上的高分别为.若,则此三角形为( )
A.等腰非直角三角形 B.等腰直角三角形
C.直角非等腰三角形 D.以上结论都不对
8.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
A.BC是△ABC的高 B.AC是△ABE的高
C.DE是△ABE的高 D.AD是△ACD的高
9.如图,在ABC中,已知点分别为边的中点,若的面积为16,则图中阴影部分的面积为( )
A.8 B.4 C.2 D.1
10.如图,AC⊥BC,CD⊥AB,DE⊥AC,垂足分别为C,D,E,则下列说法正确的是( )
A.BC是△BCD的高 B.DE=BC
C.∠CEB=∠ABC D.DE是△ACD的高
二、填空题
11.如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△ABC的面积是2,那么△A1B1C1的面积是 .
12.下列图形中,阴影部分的面积相等的是 , .
13.已知点,,,那么 .
14.如图,在中,是中线,是中点,连接,若,则 .
15.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S1﹣S2=a,则S△ABC= .
16.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△BCF=3 cm2,则S△ABC的值为 cm2.
三、解答题
17.如图:△ABC的边BC的高为AF,AC边上的高为BG,中线为AD,AF=6,BC=12,BG=5.
(1)求△ABD的面积.
(2)求AC的长.
(3)△ABD和△ACD的面积有何关系.
18.如图,三角形是由三角形经过某种平移得到的,点与点,点与点,点与点分别对应,且这六个点都在格点(小正方形的顶点)上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点和点的坐标,并说明三角形是由三角形经过怎样的平移得到的.
(2)若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为,分别求和的值.
(3)求三角形的面积.
19.如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.
(1)求证:∠AED =∠ACB;
(2)若E、F分别是AC、CD边上的中点,S△DEF=3,求S四边形ADFE .
20.如图,三角形的三个顶点坐标为,,,将这个三角形向右平移3个单位长度,再向上平移2个单位长度,得三角形,点,,分别是平移后点A,B,C的对应点.
(1)画出平移后的三角形,写出坐标( );
(2)求三角形的面积;
(3)在x轴上是否存在一点P,使三角形的面积等于三角形面积的2倍,若存在,请直接写出P点坐标,若不存在,请说明理由.
11.1.2 三角形的高、中线与角平分线
班级______ 姓名_______ 学号_____
一、选择题
1.下列说法错误的是( )
A.三角形的三条高的交点一定在三角形内部
B.三角形的三条中线的交点一定在三角形内部
C.三角形的三条角平分线的交点一定在三角形内部
D.三角形的高,中线和角平分线都有三条
2.在中,是的中线.看到图形,甲、乙、丙、丁四名同学给出四个不同的结论,其中正确的是( )
甲:
乙:
丙:
丁:
A.甲 B.乙 C.丙 D.丁
3.如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,第n次操作后,得到△AnBnCn,要使△AnBnCn的面积超过2021,则至少需要操作( )次.
A.6 B.5 C.4 D.3
4.如图已知是的中线,是的中线,若的面积为20,则的面积为( )
A.5 B.10 C.15 D.18
5.在三角形的①三条中线;②三条角平分线;③三条高中,一定相交于一点的是( )
A.①②③ B.② C.① D.①②
6.三角形的中线是( )
A.直线 B.线段 C.射线 D.以上都不正确
7.三角形中长为a,b,c的边上的高分别为.若,则此三角形为( )
A.等腰非直角三角形 B.等腰直角三角形
C.直角非等腰三角形 D.以上结论都不对
8.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
A.BC是△ABC的高 B.AC是△ABE的高
C.DE是△ABE的高 D.AD是△ACD的高
9.如图,在ABC中,已知点分别为边的中点,若的面积为16,则图中阴影部分的面积为( )
A.8 B.4 C.2 D.1
10.如图,AC⊥BC,CD⊥AB,DE⊥AC,垂足分别为C,D,E,则下列说法正确的是( )
A.BC是△BCD的高 B.DE=BC
C.∠CEB=∠ABC D.DE是△ACD的高
二、填空题
11.如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△ABC的面积是2,那么△A1B1C1的面积是 .
12.下列图形中,阴影部分的面积相等的是 , .
13.已知点,,,那么 .
14.如图,在中,是中线,是中点,连接,若,则 .
15.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S1﹣S2=a,则S△ABC= .
16.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△BCF=3 cm2,则S△ABC的值为 cm2.
三、解答题
17.如图:△ABC的边BC的高为AF,AC边上的高为BG,中线为AD,AF=6,BC=12,BG=5.
(1)求△ABD的面积.
(2)求AC的长.
(3)△ABD和△ACD的面积有何关系.
18.如图,三角形是由三角形经过某种平移得到的,点与点,点与点,点与点分别对应,且这六个点都在格点(小正方形的顶点)上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点和点的坐标,并说明三角形是由三角形经过怎样的平移得到的.
(2)若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为,分别求和的值.
(3)求三角形的面积.
19.如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.
(1)求证:∠AED =∠ACB;
(2)若E、F分别是AC、CD边上的中点,S△DEF=3,求S四边形ADFE .
20.如图,三角形的三个顶点坐标为,,,将这个三角形向右平移3个单位长度,再向上平移2个单位长度,得三角形,点,,分别是平移后点A,B,C的对应点.
(1)画出平移后的三角形,写出坐标( );
(2)求三角形的面积;
(3)在x轴上是否存在一点P,使三角形的面积等于三角形面积的2倍,若存在,请直接写出P点坐标,若不存在,请说明理由.
