第21章二次函数与反比例函数 单元复习题(含解析)2023-2024学年沪科版九年级数学上册
文档属性
| 名称 | 第21章二次函数与反比例函数 单元复习题(含解析)2023-2024学年沪科版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 302.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 12:52:20 | ||
图片预览



文档简介
沪科版九年级数学上册第21章二次函数与反比例函数 单元复习题
一、选择题
1.下列各式中,y是x的二次函数的是( )
A. B. C. D.
2.要将抛物线平移后得到抛物线,下列平移方法正确的是( )
A.向左平移1个单位,再向上平移3个单位
B.向左平移1个单位,再向下平移3个单位
C.向右平移1个单位,再向上平移3个单位
D.向右平移1个单位,再向下平移3个单位
3.二次函数的图象与轴有两个交点,则满足的条件是( )
A. B. C.且 D.
4.如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是,则该运动员此次掷铅球的成绩是( )
A.6m B.12m C.8m D.10m
5.关于反比例函数的图象,下列说法错误的是( )
A.该反比例函数图象经过点(2,-4)
B.在每一象限内,y随x的增大而增大
C.该反比例函数图象经过第一、三象限
D.该反比例函数图象关于原点对称
6.若点关于x轴的对称点恰好在反比例函数的图象上,则k的值为( )
A.6 B. C. D.
7.二次函数的二次项系数、一次项系数和常数项分别是( )
A.1,,-1 B.1,6,1 C.0,-6,1 D.0,6,-1
8.将抛物线先向左平移2个单位,再向下平移1个单位,得到的新抛物线解析式是( )
A. B.
C. D.
9.已知抛物线与x交于点,,则关于x的方程的解是( )
A., B.,
C., D.,
10.从底面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t﹣5t2,这个函数图象如图所示,则小球从第3s到第5s的运动路径长为( )
A.15m B.20m C.25m D.30m
二、填空题
11.函数是二次函数,则 .
12.如图,点A是反比例函数 的图象上的一点,过点A作AB⊥x轴,垂足为B,点C 为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是 .
13.已知函数在的最大值是1,最小值是,则m的取值范围是 .
14.从地面竖直向上跑出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是.小球运动到 时,达到最大高度.
三、解答题
15.当m为何值时,函数 是二次函数.
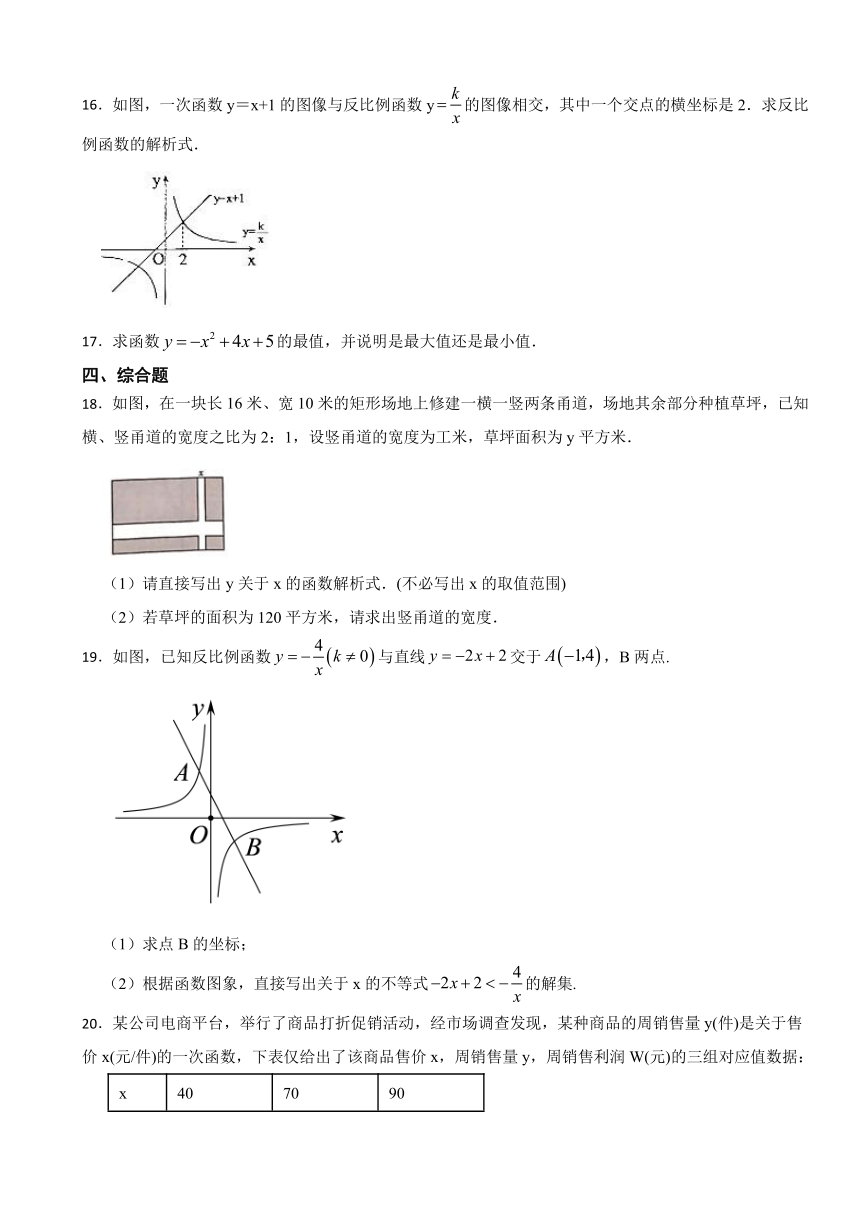
16.如图,一次函数y=x+1的图像与反比例函数y的图像相交,其中一个交点的横坐标是2.求反比例函数的解析式.
17.求函数的最值,并说明是最大值还是最小值.
四、综合题
18.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为工米,草坪面积为y平方米.
(1)请直接写出y关于x的函数解析式.(不必写出x的取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
19.如图,已知反比例函数与直线交于,B两点.
(1)求点B的坐标;
(2)根据函数图象,直接写出关于x的不等式的解集.
20.某公司电商平台,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅给出了该商品售价x,周销售量y,周销售利润W(元)的三组对应值数据:
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价为a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;
(3)因疫情原因,该商品进价提高了m(元/件) (m>0),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍然满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
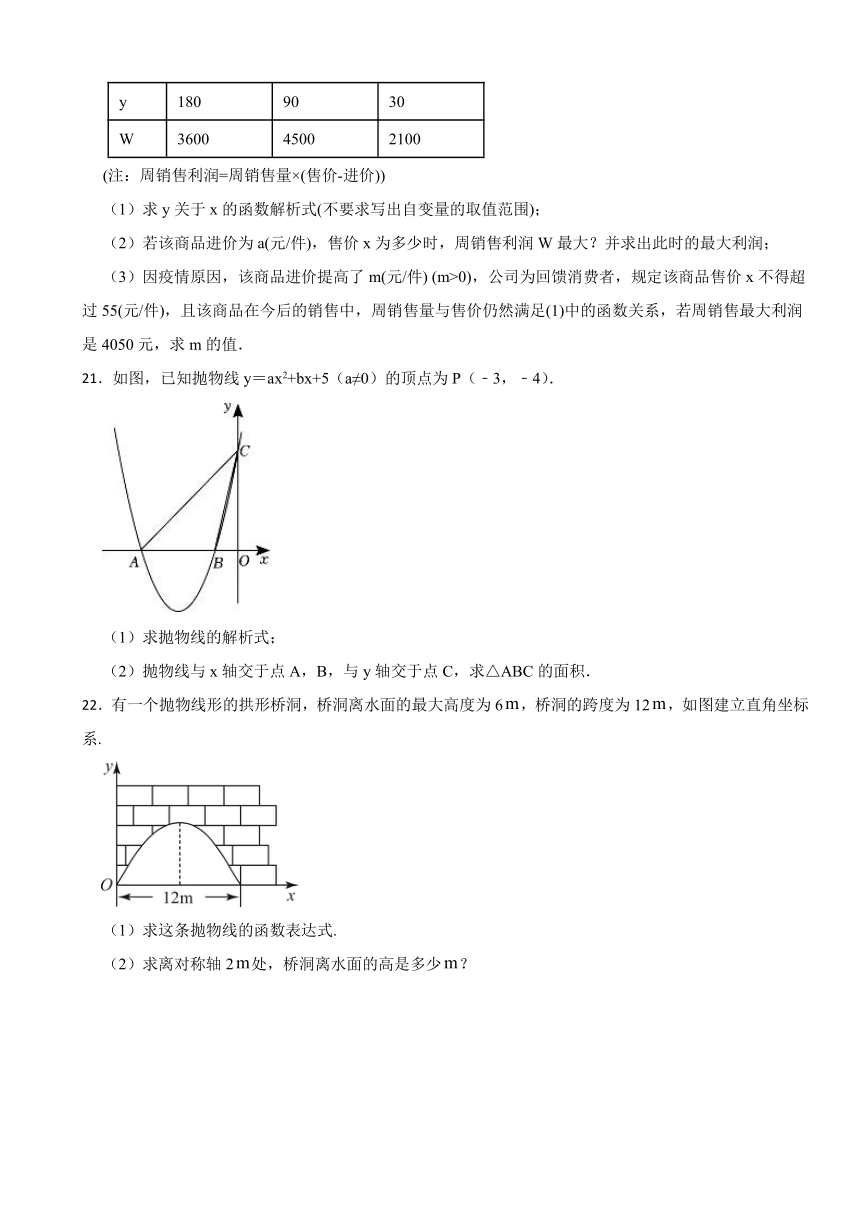
21.如图,已知抛物线y=ax2+bx+5(a≠0)的顶点为P(﹣3,﹣4).
(1)求抛物线的解析式;
(2)抛物线与x轴交于点A,B,与y轴交于点C,求△ABC的面积.
22.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为6,桥洞的跨度为12,如图建立直角坐标系.
(1)求这条抛物线的函数表达式.
(2)求离对称轴2处,桥洞离水面的高是多少?
答案解析部分
1.【答案】C
【解析】【解答】解:A.,不是函数,故该选项不符合题意;
B. ,是一次函数,故该选项不符合题意;
C.,是二次函数,符合题意;
D.,当时,不是二次函数,故该选项不符合题意.
故答案为:C.
【分析】根据二次函数的定义逐项判断即可。
2.【答案】A
【解析】【解答】解:要将抛物线平移后得到抛物线,
需要将抛物线向左平移1个单位,再向上平移3个单位,
故答案为:A.
【分析】根据抛物线的平移规律:左加右减,上加下减,可得答案.
3.【答案】C
【解析】【解答】解:对于二次函数可知,
二次函数的图象与轴有两个交点,
,
且,
故答案为:C.
【分析】根据二次函数图象与x轴有两个不同的交点,可得k≠0且b2-4ac>0,据此列出不等式组,求解即可.
4.【答案】D
【解析】【解答】解:令=0,
整理得:x2 8x 20=0,
(x 10)(x+2)=0,
解得x1=10,x2= 2(舍去),
故该运动员此次掷铅球的成绩是10m,
故答案为:D.
【分析】将y=0代入求出x的值即可。
5.【答案】C
【解析】【解答】解:A、因为2×( 4)= 8,说法正确,不符合题意;
B、因为k= 8<0,所以函数图象位于二、四象限,在每一象限内y随x的增大而增大,说法正确,不符合题意;
C、因为k= 8,所以函数图象位于二、四象限,说法错误,符合题意;
D、因为反比例函数图象关于原点对称,说法正确,不符合题意.
故答案为:C.
【分析】反比例函数(k≠0)中的k<0时,图象的两支位于第二、四象限,在每个象限内,y随x的增大而增大,图象的两支关于坐标原点对称;反比例函数图象上任意一点的横纵坐标的乘积都等于常数k,据此一一判断得出答案.
6.【答案】D
【解析】【解答】解:∵点与点关于x轴对称,
∴点,
又∵点在反比例函数的图象上,
∴,
故答案为:D.
【分析】关于x轴对称的点:横坐标相同,纵坐标互为相反数,据此可得点A′的坐标,然后代入y=中进行计算可得k的值.
7.【答案】A
【解析】【解答】解:二次函数,
二次项系数、一次项系数、常数项分别是1,-6,-1.
故答案为:A.
【分析】利用一元二次方程的二次项系数、一次项系数和常数项的定义求解即可。
8.【答案】B
【解析】【解答】解:将抛物线先向左平移2个单位,再向下平移1个单位,得到的新抛物线解析式是,即,
故答案为:B.
【分析】根据平移规则“左加右减,上加下减”进行解答.
9.【答案】C
【解析】【解答】解:∵与交于点,两点,
∴方程个根为,,
故答案为:C.
【分析】 关于x的方程的解即是抛物线与x轴交点的横坐标.
10.【答案】B
【解析】【解答】解:∵小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t﹣5t2,
当t=3时,h=30×3﹣5×32=90-45=45m,
当t=5时,h=30×5﹣5×52=150-125=25m,
∴小球从第3s到第5s的运动路径长为45m-25m=20m.
故答案为:B.
【分析】将t=3和t=5分别代入解析式求出h的值,再求解即可。
11.【答案】1
【解析】【解答】解:函数是二次函数,
,
解得:,
故答案为:1.
【分析】二次函数的一般形式为:y=ax2+bx+c(a、b、c为常数且a≠0),则2m=2,求解可得m的值.
12.【答案】-6
【解析】【解答】解:连接OA,
∵AB⊥x轴,
∴∠ABO=90°=∠BOC,
∴OC∥AB,
∴S△AOB=S△ABC=3,
∴,
∵k<0,
∴k=-6.
故答案为:-6
【分析】连接OA,利用同底等高的两个三角形的面积相等,可得到△AOB的面积,再根据反比例函数的几何意义,可求出k的值.
13.【答案】
【解析】【解答】解:,
∵
∴当时,函数有最小值为:,
当时:,
由抛物线的对称性可知:当时,,
∵函数在的最大值是1,最小值是,
∴;
故答案为:.
【分析】将二次函数的解析式化为顶点式,得到开口方向以及对称轴、最小值,令x=1,求出y的值,由抛物线的对称性可知:当x=-2时,y=1,然后结合题意可得m的范围.
14.【答案】6
【解析】【解答】解:,
∴对称轴为,抛物线开口向下,
在对称轴的左边,随的增大而增大,
∵
∴当时,达到最大高度,
故答案为:6.
【分析】将变形为=,再利用二次函数的性质求解即可。
15.【答案】解:∵函数 是二次函数
∴
解得:m=3
即当m=3时,函数 是二次函数.
【解析】【分析】根据二次函数的定义即可求出结论.
16.【答案】解:当x=2时,代入y=x + 1,得y=3.
把点(2,3)代入,得k=6
∴
【解析】【分析】先将x=2代入一次函数解析式求出交点坐标,再将交点坐标代入反比例函数解析式求出k的值即可得到反比例函数解析式。
17.【答案】解:在本函数中
抛物线开口向下,有最大值,
将 进行配方,
得 ,
当 时,
,为最大值.
【解析】【分析】将二次函数的一般式化为顶点式,再利用二次函数的性质求解即可。
18.【答案】(1)y =2 x2 -42x +160
(2)解:依题意,得 2 x2 -42x +160=120 ,
整理,得 x 2 -21 x +20=0 ,
解得 x 1 =1 , x 2 =20.
当 x =1 时, 10-2 x =8>0 ,符合题意 .
当 x =20 时, 10-2 x =-30<0 ,不符合题意,舍去 .
答:竖甬道的宽度为 1 米
【解析】【解答】解:(1)横甬道的宽度为 2 x 米,剩余部分可合成长( 16- x )米,宽( 10-2 x )米的矩形 .依题意,得 y = ( 16- x )( 10-2 x ) =2 x 2 -42 x +160.
【分析】(1)根据题意得出横甬道的宽度为2x米,剩余部分合成长为(16- x )米,宽为( 10-2x )米的矩形,利用矩形的面积公式得出y=(16- x )(10- 2x ),进行化简即可得出答案;
(2)根据题意列出方程,解方程求出x的值,再进行检验,即可得出答案.
19.【答案】(1)解:联列方程组:
,
解得或;
∴B的坐标为:;
(2)解:由图可知,当或时,反比例函数的图象在一次函数图象的上方,
所以的解集为:或.
【解析】【分析】(1)联立一次函数与反比例函数的解析式求出x、y的值,可得点B的坐标;
(2)根据图象,找出反比例函数的图象在一次函数图象的上方部分所对应的x的范围即可.
20.【答案】(1)解:设y=kx+b.由表中数据,得
解得
∴y=-3x+300.
(2)解:由表格第二列可知3600=180(40-a).解得a=20.
∴W=y(x-a)=(-3x+300) (x-20)
=-3(x2-120x+2000)
=-3(x-60)2+4800.
∵-3<0,∴当x=60时,W最大,最大利润是4800元.
(3)解:W'=y(x-a-m)=(-3x+300) (x-20-m)
=-3[x2-(120+m)x+100(20+m)].
∵抛物线的开口向下,对称轴方程x=>60,且0∴当x=55时,W'最大.
∵W'最大= 4050,
∴(- 3×55+300) (55-20-m)=4050.
解得m=5.
【解析】【分析】(1)设该一次函数的解析式,并根据待定系数法进行求解。
(2)利润=(售价-进价)×数量,结合题干信息得到关于x的二次函数,将该二次函数写成顶点式的解析式进行分析。
(3)利润=(售价-进价)×数量,结合题干信息得到关于x的二次函数,根据二次函数的性质、对称轴及x的取值范围可找到,当x=55时周销售利润最大,进一步求解。
21.【答案】(1)解:∵抛物线y=ax2+bx+5(a≠0)的顶点为P(﹣3,﹣4),
∴y=a(x+3)2﹣4,
∵y=a(x+3)2﹣4=ax2+6ax+9a﹣4,
∴
解得
∴抛物线的解析式为y=x2+6x+5;
(2)解:在y=x2+6x+5中,
令y=0,则x2+6x+5=0,
解得x=﹣1或x=﹣5,
∴A(﹣5,0),B(﹣1,0),
令x=0,则y=5,
∴C(0,5),
∴AB=4,OC=5,
∴S△ABC= AB OC= =10.
【解析】【分析】(1)利用点P是抛物线的顶点坐标,因此设y=a(x+3)2﹣4ax2+bx+5,利用对应项的系数相等,可得到关于a,b的方程组,解方程组求出a,b的值,可得到抛物线的解析式.
(2)由y=0,可得到关于x的方程,解方程求出x的值,可得到点A,B的坐标,由x=0可求出y的值,可得到点C的坐标;由此可得到AB和OC的长,再利用三角形的面积公式可求出△ABC的面积.
22.【答案】(1)解:由题意可得,抛物线顶点坐标为,
设抛物线解析式为,
∵抛物线过点,
∴,解得,
∴这条抛物线所对应的函数表达式为
(2)解:由题意可知该抛物线的对称轴为,则对称轴右边2处为,
将代入,
可得,解得,
答:离对称轴2处,桥洞离水面的高是.
【解析】【分析】(1)根据顶点坐标可设抛物线的解析式为y=a(x-6)2+6,将(0,0)代入求出a的值,据此可得抛物线的解析式;
(2)根据抛物线的解析式可得对称轴为直线x=6,则对称轴右边2m处为x=8,将x=8代入抛物线解析式中求出y的值,据此解答.
一、选择题
1.下列各式中,y是x的二次函数的是( )
A. B. C. D.
2.要将抛物线平移后得到抛物线,下列平移方法正确的是( )
A.向左平移1个单位,再向上平移3个单位
B.向左平移1个单位,再向下平移3个单位
C.向右平移1个单位,再向上平移3个单位
D.向右平移1个单位,再向下平移3个单位
3.二次函数的图象与轴有两个交点,则满足的条件是( )
A. B. C.且 D.
4.如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是,则该运动员此次掷铅球的成绩是( )
A.6m B.12m C.8m D.10m
5.关于反比例函数的图象,下列说法错误的是( )
A.该反比例函数图象经过点(2,-4)
B.在每一象限内,y随x的增大而增大
C.该反比例函数图象经过第一、三象限
D.该反比例函数图象关于原点对称
6.若点关于x轴的对称点恰好在反比例函数的图象上,则k的值为( )
A.6 B. C. D.
7.二次函数的二次项系数、一次项系数和常数项分别是( )
A.1,,-1 B.1,6,1 C.0,-6,1 D.0,6,-1
8.将抛物线先向左平移2个单位,再向下平移1个单位,得到的新抛物线解析式是( )
A. B.
C. D.
9.已知抛物线与x交于点,,则关于x的方程的解是( )
A., B.,
C., D.,
10.从底面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t﹣5t2,这个函数图象如图所示,则小球从第3s到第5s的运动路径长为( )
A.15m B.20m C.25m D.30m
二、填空题
11.函数是二次函数,则 .
12.如图,点A是反比例函数 的图象上的一点,过点A作AB⊥x轴,垂足为B,点C 为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是 .
13.已知函数在的最大值是1,最小值是,则m的取值范围是 .
14.从地面竖直向上跑出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是.小球运动到 时,达到最大高度.
三、解答题
15.当m为何值时,函数 是二次函数.
16.如图,一次函数y=x+1的图像与反比例函数y的图像相交,其中一个交点的横坐标是2.求反比例函数的解析式.
17.求函数的最值,并说明是最大值还是最小值.
四、综合题
18.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为工米,草坪面积为y平方米.
(1)请直接写出y关于x的函数解析式.(不必写出x的取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
19.如图,已知反比例函数与直线交于,B两点.
(1)求点B的坐标;
(2)根据函数图象,直接写出关于x的不等式的解集.
20.某公司电商平台,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅给出了该商品售价x,周销售量y,周销售利润W(元)的三组对应值数据:
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价为a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;
(3)因疫情原因,该商品进价提高了m(元/件) (m>0),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍然满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
21.如图,已知抛物线y=ax2+bx+5(a≠0)的顶点为P(﹣3,﹣4).
(1)求抛物线的解析式;
(2)抛物线与x轴交于点A,B,与y轴交于点C,求△ABC的面积.
22.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为6,桥洞的跨度为12,如图建立直角坐标系.
(1)求这条抛物线的函数表达式.
(2)求离对称轴2处,桥洞离水面的高是多少?
答案解析部分
1.【答案】C
【解析】【解答】解:A.,不是函数,故该选项不符合题意;
B. ,是一次函数,故该选项不符合题意;
C.,是二次函数,符合题意;
D.,当时,不是二次函数,故该选项不符合题意.
故答案为:C.
【分析】根据二次函数的定义逐项判断即可。
2.【答案】A
【解析】【解答】解:要将抛物线平移后得到抛物线,
需要将抛物线向左平移1个单位,再向上平移3个单位,
故答案为:A.
【分析】根据抛物线的平移规律:左加右减,上加下减,可得答案.
3.【答案】C
【解析】【解答】解:对于二次函数可知,
二次函数的图象与轴有两个交点,
,
且,
故答案为:C.
【分析】根据二次函数图象与x轴有两个不同的交点,可得k≠0且b2-4ac>0,据此列出不等式组,求解即可.
4.【答案】D
【解析】【解答】解:令=0,
整理得:x2 8x 20=0,
(x 10)(x+2)=0,
解得x1=10,x2= 2(舍去),
故该运动员此次掷铅球的成绩是10m,
故答案为:D.
【分析】将y=0代入求出x的值即可。
5.【答案】C
【解析】【解答】解:A、因为2×( 4)= 8,说法正确,不符合题意;
B、因为k= 8<0,所以函数图象位于二、四象限,在每一象限内y随x的增大而增大,说法正确,不符合题意;
C、因为k= 8,所以函数图象位于二、四象限,说法错误,符合题意;
D、因为反比例函数图象关于原点对称,说法正确,不符合题意.
故答案为:C.
【分析】反比例函数(k≠0)中的k<0时,图象的两支位于第二、四象限,在每个象限内,y随x的增大而增大,图象的两支关于坐标原点对称;反比例函数图象上任意一点的横纵坐标的乘积都等于常数k,据此一一判断得出答案.
6.【答案】D
【解析】【解答】解:∵点与点关于x轴对称,
∴点,
又∵点在反比例函数的图象上,
∴,
故答案为:D.
【分析】关于x轴对称的点:横坐标相同,纵坐标互为相反数,据此可得点A′的坐标,然后代入y=中进行计算可得k的值.
7.【答案】A
【解析】【解答】解:二次函数,
二次项系数、一次项系数、常数项分别是1,-6,-1.
故答案为:A.
【分析】利用一元二次方程的二次项系数、一次项系数和常数项的定义求解即可。
8.【答案】B
【解析】【解答】解:将抛物线先向左平移2个单位,再向下平移1个单位,得到的新抛物线解析式是,即,
故答案为:B.
【分析】根据平移规则“左加右减,上加下减”进行解答.
9.【答案】C
【解析】【解答】解:∵与交于点,两点,
∴方程个根为,,
故答案为:C.
【分析】 关于x的方程的解即是抛物线与x轴交点的横坐标.
10.【答案】B
【解析】【解答】解:∵小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t﹣5t2,
当t=3时,h=30×3﹣5×32=90-45=45m,
当t=5时,h=30×5﹣5×52=150-125=25m,
∴小球从第3s到第5s的运动路径长为45m-25m=20m.
故答案为:B.
【分析】将t=3和t=5分别代入解析式求出h的值,再求解即可。
11.【答案】1
【解析】【解答】解:函数是二次函数,
,
解得:,
故答案为:1.
【分析】二次函数的一般形式为:y=ax2+bx+c(a、b、c为常数且a≠0),则2m=2,求解可得m的值.
12.【答案】-6
【解析】【解答】解:连接OA,
∵AB⊥x轴,
∴∠ABO=90°=∠BOC,
∴OC∥AB,
∴S△AOB=S△ABC=3,
∴,
∵k<0,
∴k=-6.
故答案为:-6
【分析】连接OA,利用同底等高的两个三角形的面积相等,可得到△AOB的面积,再根据反比例函数的几何意义,可求出k的值.
13.【答案】
【解析】【解答】解:,
∵
∴当时,函数有最小值为:,
当时:,
由抛物线的对称性可知:当时,,
∵函数在的最大值是1,最小值是,
∴;
故答案为:.
【分析】将二次函数的解析式化为顶点式,得到开口方向以及对称轴、最小值,令x=1,求出y的值,由抛物线的对称性可知:当x=-2时,y=1,然后结合题意可得m的范围.
14.【答案】6
【解析】【解答】解:,
∴对称轴为,抛物线开口向下,
在对称轴的左边,随的增大而增大,
∵
∴当时,达到最大高度,
故答案为:6.
【分析】将变形为=,再利用二次函数的性质求解即可。
15.【答案】解:∵函数 是二次函数
∴
解得:m=3
即当m=3时,函数 是二次函数.
【解析】【分析】根据二次函数的定义即可求出结论.
16.【答案】解:当x=2时,代入y=x + 1,得y=3.
把点(2,3)代入,得k=6
∴
【解析】【分析】先将x=2代入一次函数解析式求出交点坐标,再将交点坐标代入反比例函数解析式求出k的值即可得到反比例函数解析式。
17.【答案】解:在本函数中
抛物线开口向下,有最大值,
将 进行配方,
得 ,
当 时,
,为最大值.
【解析】【分析】将二次函数的一般式化为顶点式,再利用二次函数的性质求解即可。
18.【答案】(1)y =2 x2 -42x +160
(2)解:依题意,得 2 x2 -42x +160=120 ,
整理,得 x 2 -21 x +20=0 ,
解得 x 1 =1 , x 2 =20.
当 x =1 时, 10-2 x =8>0 ,符合题意 .
当 x =20 时, 10-2 x =-30<0 ,不符合题意,舍去 .
答:竖甬道的宽度为 1 米
【解析】【解答】解:(1)横甬道的宽度为 2 x 米,剩余部分可合成长( 16- x )米,宽( 10-2 x )米的矩形 .依题意,得 y = ( 16- x )( 10-2 x ) =2 x 2 -42 x +160.
【分析】(1)根据题意得出横甬道的宽度为2x米,剩余部分合成长为(16- x )米,宽为( 10-2x )米的矩形,利用矩形的面积公式得出y=(16- x )(10- 2x ),进行化简即可得出答案;
(2)根据题意列出方程,解方程求出x的值,再进行检验,即可得出答案.
19.【答案】(1)解:联列方程组:
,
解得或;
∴B的坐标为:;
(2)解:由图可知,当或时,反比例函数的图象在一次函数图象的上方,
所以的解集为:或.
【解析】【分析】(1)联立一次函数与反比例函数的解析式求出x、y的值,可得点B的坐标;
(2)根据图象,找出反比例函数的图象在一次函数图象的上方部分所对应的x的范围即可.
20.【答案】(1)解:设y=kx+b.由表中数据,得
解得
∴y=-3x+300.
(2)解:由表格第二列可知3600=180(40-a).解得a=20.
∴W=y(x-a)=(-3x+300) (x-20)
=-3(x2-120x+2000)
=-3(x-60)2+4800.
∵-3<0,∴当x=60时,W最大,最大利润是4800元.
(3)解:W'=y(x-a-m)=(-3x+300) (x-20-m)
=-3[x2-(120+m)x+100(20+m)].
∵抛物线的开口向下,对称轴方程x=>60,且0
∵W'最大= 4050,
∴(- 3×55+300) (55-20-m)=4050.
解得m=5.
【解析】【分析】(1)设该一次函数的解析式,并根据待定系数法进行求解。
(2)利润=(售价-进价)×数量,结合题干信息得到关于x的二次函数,将该二次函数写成顶点式的解析式进行分析。
(3)利润=(售价-进价)×数量,结合题干信息得到关于x的二次函数,根据二次函数的性质、对称轴及x的取值范围可找到,当x=55时周销售利润最大,进一步求解。
21.【答案】(1)解:∵抛物线y=ax2+bx+5(a≠0)的顶点为P(﹣3,﹣4),
∴y=a(x+3)2﹣4,
∵y=a(x+3)2﹣4=ax2+6ax+9a﹣4,
∴
解得
∴抛物线的解析式为y=x2+6x+5;
(2)解:在y=x2+6x+5中,
令y=0,则x2+6x+5=0,
解得x=﹣1或x=﹣5,
∴A(﹣5,0),B(﹣1,0),
令x=0,则y=5,
∴C(0,5),
∴AB=4,OC=5,
∴S△ABC= AB OC= =10.
【解析】【分析】(1)利用点P是抛物线的顶点坐标,因此设y=a(x+3)2﹣4ax2+bx+5,利用对应项的系数相等,可得到关于a,b的方程组,解方程组求出a,b的值,可得到抛物线的解析式.
(2)由y=0,可得到关于x的方程,解方程求出x的值,可得到点A,B的坐标,由x=0可求出y的值,可得到点C的坐标;由此可得到AB和OC的长,再利用三角形的面积公式可求出△ABC的面积.
22.【答案】(1)解:由题意可得,抛物线顶点坐标为,
设抛物线解析式为,
∵抛物线过点,
∴,解得,
∴这条抛物线所对应的函数表达式为
(2)解:由题意可知该抛物线的对称轴为,则对称轴右边2处为,
将代入,
可得,解得,
答:离对称轴2处,桥洞离水面的高是.
【解析】【分析】(1)根据顶点坐标可设抛物线的解析式为y=a(x-6)2+6,将(0,0)代入求出a的值,据此可得抛物线的解析式;
(2)根据抛物线的解析式可得对称轴为直线x=6,则对称轴右边2m处为x=8,将x=8代入抛物线解析式中求出y的值,据此解答.
