第11章 三角形单元测试卷（含答案）

第11章 三角形 测试卷
(考试时间：100分钟，赋分：120分)
姓名：________　　班级：________　　分数：________
一、选择题(本大题共10小题,每小题3分,满分30分)
题　号 1 2 3 4 5 6 7 8 9 10
答　案
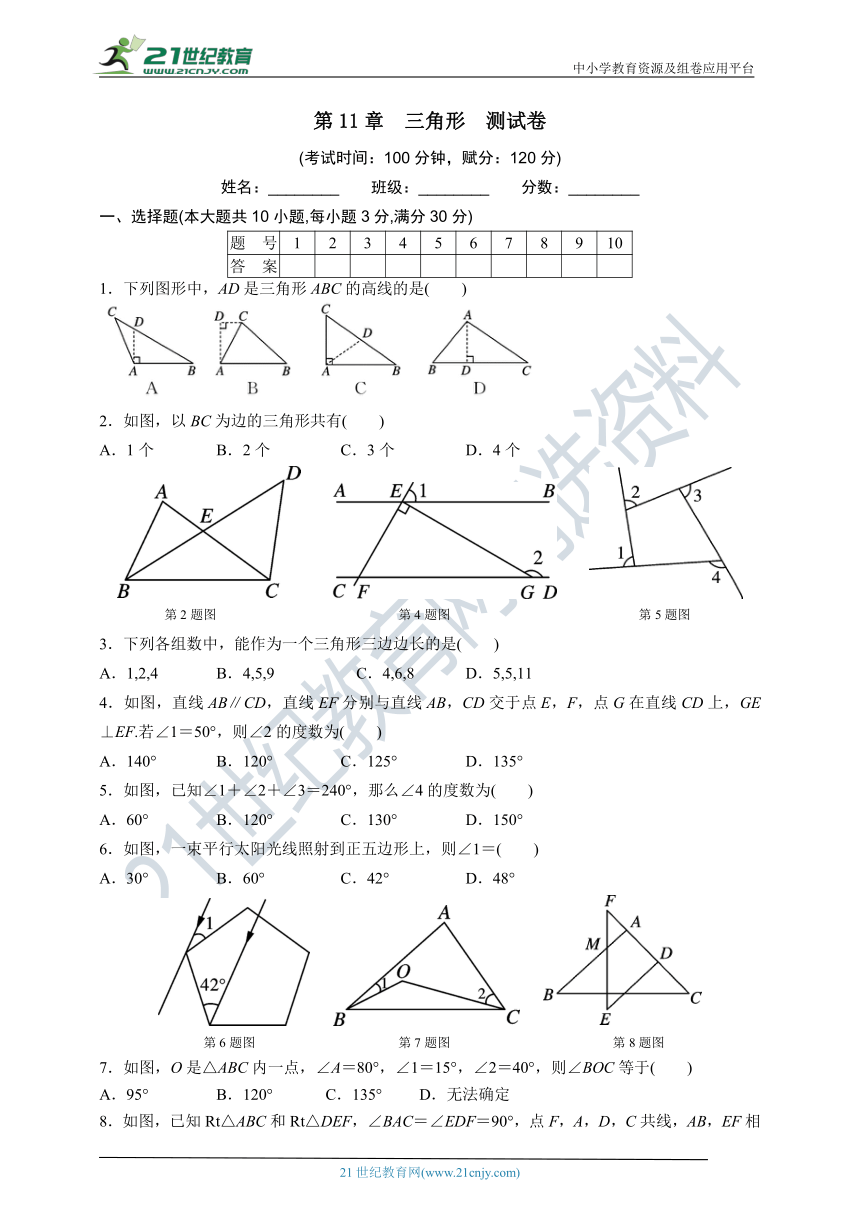
1．下列图形中，AD是三角形ABC的高线的是(　　)
2．如图，以BC为边的三角形共有(　　)
A．1个 B．2个 C．3个 D．4个
第2题图 第4题图 第5题图
3．下列各组数中，能作为一个三角形三边边长的是(　　)
A．1,2,4 B．4,5,9 C．4,6,8 D．5,5,11
4．如图，直线AB∥CD，直线EF分别与直线AB，CD交于点E，F，点G在直线CD上，GE⊥EF.若∠1＝50°，则∠2的度数为(　　)
A．140° B．120° C．125° D．135°
5．如图，已知∠1＋∠2＋∠3＝240°，那么∠4的度数为(　　)
A．60° B．120° C．130° D．150°
6．如图，一束平行太阳光线照射到正五边形上，则∠1＝(　　)
A．30° B．60° C．42° D．48°
第6题图 第7题图 第8题图
7．如图，O是△ABC内一点，∠A＝80°，∠1＝15°，∠2＝40°，则∠BOC等于(　　)
A．95° B．120° C．135° D．无法确定
8．如图，已知Rt△ABC和Rt△DEF，∠BAC＝∠EDF＝90°，点F，A，D，C共线，AB，EF相交于点M，且EF⊥BC，则图中与∠E相等的角有(　　)
A．5个 B．4个 C．3个 D．2个
9．如图，点D，E，G分别为△ABC的边AC，AB，BC上的点，连接DE，EG，将△ABC沿DE，EG翻折，顶点A，B均落在△ABC的内部一点F处，且EA与EB重合于线段EF，若∠C＝54°，∠BGE＝66°，则∠ADE的度数为(　　)
A．77° B．78° C．79° D．80°
第9题图 第10题图 第13题图
10．如图，∠ABD，∠ACD的平分线交于点P，若∠A＝60°，∠D＝20°，则∠P的度数为(　　)
A．15° B．20° C．25° D．30°
二、填空题(本大题共8小题,每小题3分,满分24分)
11．人站在晃动的公共汽车上，若两腿分开站立，还需伸出一只手抓住栏杆才能站稳，这是利用了_____________________.
12．一个多边形的每一个外角都等于40°，则从这个多边形的一个顶点出发共有___条对角线．
13．将一副直角三角尺按如图所示方式放置，使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边重合，则∠1的度数为_________.
14．已知a，b，c是△ABC的三边长，化简：|a＋b－c|－|b－a－c|＋2c＝______.
15．如图，∠B＝∠C，DE⊥BC于点E，EF⊥AB于点F，若∠ADE＝145°，则∠FED＝_________.
第15题图 第17题图 第18题图
16．如图，△ABC的面积是2，AD是BC边上的中线，AE＝AD，BF＝EF，则△DEF的面积为___.
17．如图，在七边形ABCDEFG中，AB，ED的延长线交于点O.若与∠1，∠2，∠3，∠4相邻的四个外角的和等于230°，则∠BOD的度数为_________.
18．AE是△ABC的角平分线，AD是BC边上的高，且∠B＝40°，∠ACD＝70°，则∠DAE的度数为_____________________.
三、解答题(共66分)
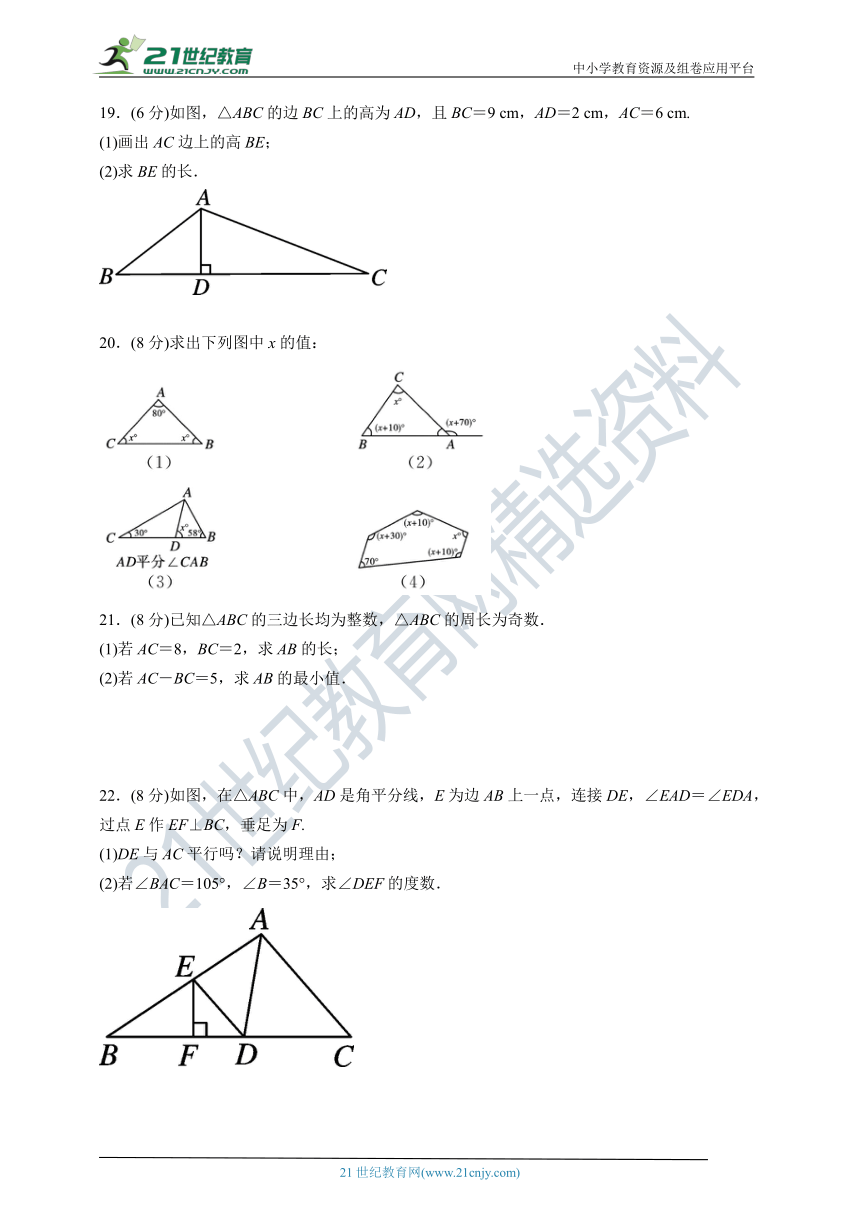
19．(6分)如图，△ABC的边BC上的高为AD，且BC＝9 cm，AD＝2 cm，AC＝6 cm.
(1)画出AC边上的高BE；
(2)求BE的长．
20．(8分)求出下列图中x的值：
21．(8分)已知△ABC的三边长均为整数，△ABC的周长为奇数．
(1)若AC＝8，BC＝2，求AB的长；
(2)若AC－BC＝5，求AB的最小值．
22．(8分)如图，在△ABC中，AD是角平分线，E为边AB上一点，连接DE，∠EAD＝∠EDA，过点E作EF⊥BC，垂足为F.
(1)DE与AC平行吗？请说明理由；
(2)若∠BAC＝105°，∠B＝35°，求∠DEF的度数．
23.(10分)如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G的度数．
24．(12分)(1)如图①，在△ABC中，∠B＝40°，∠C＝80°，AD⊥BC于点D，AE平分∠BAC，求∠EAD的度数；
(2)在上题中，“∠B＝40°，∠C＝80°”改为“∠C>∠B”，其他条件不变，你能找出∠EAD与∠B，∠C之间的数量关系吗？
(3)如图②，AE平分∠BAC，F为AE上一点，FM⊥BC于点M，这时∠EFM与∠B，∠C之间又有何数量关系？为什么？
25．(14分)已知在四边形ABCD中，∠A＝∠C＝90°.
(1)∠ABC＋∠ADC＝_________°；
(2)如图①，若DE平分∠ADC交BC于点E，BF平分四边形ABCD的外角∠CBM，写出DE与BF的位置关系，并证明；
(3)如图②，若BF，DE分别平分四边形ABCD的外角∠CBM，∠CDN，写出BF与DE的位置关系，并证明．
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题(本大题共10小题,每小题3分,满分30分)
题　号 1 2 3 4 5 6 7 8 9 10
答　案 D C C A B A C C B B
1．下列图形中，AD是三角形ABC的高线的是(　　)
2．如图，以BC为边的三角形共有(　　)
A．1个 B．2个 C．3个 D．4个
第2题图 第4题图 第5题图
3．下列各组数中，能作为一个三角形三边边长的是(　　)
A．1,2,4 B．4,5,9 C．4,6,8 D．5,5,11
4．如图，直线AB∥CD，直线EF分别与直线AB，CD交于点E，F，点G在直线CD上，GE⊥EF.若∠1＝50°，则∠2的度数为(　　)
A．140° B．120° C．125° D．135°
5．如图，已知∠1＋∠2＋∠3＝240°，那么∠4的度数为(　　)
A．60° B．120° C．130° D．150°
6．如图，一束平行太阳光线照射到正五边形上，则∠1＝(　　)
A．30° B．60° C．42° D．48°
第6题图 第7题图 第8题图
7．如图，O是△ABC内一点，∠A＝80°，∠1＝15°，∠2＝40°，则∠BOC等于(　　)
A．95° B．120° C．135° D．无法确定
8．如图，已知Rt△ABC和Rt△DEF，∠BAC＝∠EDF＝90°，点F，A，D，C共线，AB，EF相交于点M，且EF⊥BC，则图中与∠E相等的角有(　 　)
A．5个 B．4个 C．3个 D．2个
9．如图，点D，E，G分别为△ABC的边AC，AB，BC上的点，连接DE，EG，将△ABC沿DE，EG翻折，顶点A，B均落在△ABC的内部一点F处，且EA与EB重合于线段EF，若∠C＝54°，∠BGE＝66°，则∠ADE的度数为(　　)
A．77° B．78° C．79° D．80°
第9题图 第10题图 第13题图
10．如图，∠ABD，∠ACD的平分线交于点P，若∠A＝60°，∠D＝20°，则∠P的度数为(　 　)
A．15° B．20° C．25° D．30°
二、填空题(本大题共8小题,每小题3分,满分24分)
11．人站在晃动的公共汽车上，若两腿分开站立，还需伸出一只手抓住栏杆才能站稳，这是利用了_____________________.
【答案】三角形的稳定性
12．一个多边形的每一个外角都等于40°，则从这个多边形的一个顶点出发共有___条对角线．
【答案】6
13．将一副直角三角尺按如图所示方式放置，使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边重合，则∠1的度数为_________.
【答案】75°
14．已知a，b，c是△ABC的三边长，化简：|a＋b－c|－|b－a－c|＋2c＝______.
【答案】2b
15．如图，∠B＝∠C，DE⊥BC于点E，EF⊥AB于点F，若∠ADE＝145°，则∠FED＝_________.
【答案】55°
第15题图 第17题图 第18题图
16．如图，△ABC的面积是2，AD是BC边上的中线，AE＝AD，BF＝EF，则△DEF的面积为___.
【答案】
17．如图，在七边形ABCDEFG中，AB，ED的延长线交于点O.若与∠1，∠2，∠3，∠4相邻的四个外角的和等于230°，则∠BOD的度数为_________.
【答案】50°
18．AE是△ABC的角平分线，AD是BC边上的高，且∠B＝40°，∠ACD＝70°，则∠DAE的度数为_____________________.
【答案】15°或35°
三、解答题(共66分)
19．(6分)如图，△ABC的边BC上的高为AD，且BC＝9 cm，AD＝2 cm，AC＝6 cm.
(1)画出AC边上的高BE；
(2)求BE的长．
解：(1)图略．
(2)∵S△ABC＝·AD·BC＝·BE·AC，
∴BE＝＝3(cm)．
20．(8分)求出下列图中x的值：
解：(1)x＝50.(2)x＝60.(3)x＝76.(4)x＝105.
21．(8分)已知△ABC的三边长均为整数，△ABC的周长为奇数．
(1)若AC＝8，BC＝2，求AB的长；
(2)若AC－BC＝5，求AB的最小值．
解：(1)由三角形的三边关系，得6又∵△ABC的周长为奇数，而AC，BC的长为偶数，
∴AB的长为奇数，故AB＝7或9.
(2)∵AC－BC＝5，
∴AC，BC的长中一个奇数、一个偶数．
又∵△ABC的周长为奇数，故AB的长为偶数，
由AB>AC－BC＝5，得AB的长的最小值为6.
22．(8分)如图，在△ABC中，AD是角平分线，E为边AB上一点，连接DE，∠EAD＝∠EDA，过点E作EF⊥BC，垂足为F.
(1)DE与AC平行吗？请说明理由；
(2)若∠BAC＝105°，∠B＝35°，求∠DEF的度数．
解：(1)DE∥AC.
理由如下：∵AD平分∠BAC，
∴∠BAD＝∠CAD.
∵∠EAD＝∠EDA，
∴∠CAD＝∠EDA，∴DE∥AC.
(2)∵∠B＋∠C＋∠BAC＝180°，
∴∠C＝180°－105°－35°＝40°.
∵DE∥AC，∴∠EDF＝∠C＝40°.
∵EF⊥BD，∴∠EFD＝90°，
∴∠DEF＝90°－∠EDF＝90°－40°＝50°.
23.(10分)如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G的度数．
解：在四边形BCDM中，∠C＋∠B＋∠D＋∠2＝360°.
在四边形MEFN中，
∠1＋∠3＋∠E＋∠F＝360°.
∵∠1＝∠A＋∠G，
∠2＋∠3＝180°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＝(∠A＋∠G)＋(∠B＋∠C＋∠D＋∠2)＋(∠E＋∠F＋∠1＋∠3)－∠2－∠1－∠3＝∠1＋360°＋360°－180°－∠1＝540°.
24．(12分)(1)如图①，在△ABC中，∠B＝40°，∠C＝80°，AD⊥BC于点D，AE平分∠BAC，求∠EAD的度数；
(2)在上题中，“∠B＝40°，∠C＝80°”改为“∠C>∠B”，其他条件不变，你能找出∠EAD与∠B，∠C之间的数量关系吗？
(3)如图②，AE平分∠BAC，F为AE上一点，FM⊥BC于点M，这时∠EFM与∠B，∠C之间又有何数量关系？为什么？
解：(1)∠EAD＝20°.
(2)∠EAD＝(∠C－∠B)．
(3)∠EFM＝(∠C－∠B)．证明略．
25．(14分)已知在四边形ABCD中，∠A＝∠C＝90°.
(1)∠ABC＋∠ADC＝_________°；【答案】180
(2)如图①，若DE平分∠ADC交BC于点E，BF平分四边形ABCD的外角∠CBM，写出DE与BF的位置关系，并证明；
(3)如图②，若BF，DE分别平分四边形ABCD的外角∠CBM，∠CDN，写出BF与DE的位置关系，并证明．
解：(2)DE⊥BF.证明如下：
如图①，延长DE交BF于点G，
∵∠ABC＋∠ADC＝180°，∠ABC＋∠CBM＝180°，
∴∠ADC＝∠CBM.
∵DE平分∠ADC，BF平分∠CBM，
∴∠CDE＝∠ADC，∠EBF＝∠CBM，
∴∠CDE＝∠EBF.
∵∠DEC＝∠BEG，
∴∠EGB＝∠C＝90°，
∴DE⊥BF.
(3)DE∥BF.证明如下：
如图②，连接BD，
∵∠ABC＋∠ADC＝180°，
∴∠NDC＋∠MBC＝180°.
∵BF，DE分别平分∠CBM，∠CDN，
∴∠EDC＋∠CBF＝90°.
在△CDB中，∵∠C＝90°，
∴∠CDB＋∠CBD＝90°，
∴∠EDC＋∠CDB＋∠CBD＋∠FBC＝180°，
即∠BDE＋∠DBF＝180°，
∴DE∥BF.