【单元复习指南】第八单元 数学广角——数与形-六年级上册数学单元复习精编讲义·人教版(含答案)
文档属性
| 名称 | 【单元复习指南】第八单元 数学广角——数与形-六年级上册数学单元复习精编讲义·人教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 00:00:00 | ||
图片预览

文档简介
人教版六年级上册数学单元复习精编讲义
第八单元 数学广角——数与形
单元知识要点
通过自主探究发现图形中隐藏着的数的规律,并体会运用发现的规律解决问题的简捷性。能利用数形结合思想来解决一些与数有关的问题。体会数结合思想的重要性,训练思维的灵活性和准确性。
知识点归纳总结
1.2+4+6+8+10+12+14+16+18+20=(110)
规律∶从 2开始的 n个连续偶数的和等于n×(n+1)。
10×(10+1)=10×11=110
2.1=12=1
1+3=22=(4)
1+3+5=32=(9)
1+3+5+7=42=(16)
1+3+5+7+9=52=(25)
1+3+5+7+9+11=62=(36)
1+3+5+7+9+11+13=72=(49)
1+3+5+7+9+11+13+15=82=(64)
1+3+5+7+9+11+13+15+17=92=(81)
1+3+5+7+9+11+13+15+17+19=102=(100)
从1开始的连续奇数的和正好是这串数个数的平方。即:从1开始的n个连续奇数相加的和可以用n2表示,即1+3+5+7+9+…+(2n-1)=n2。
典型例题
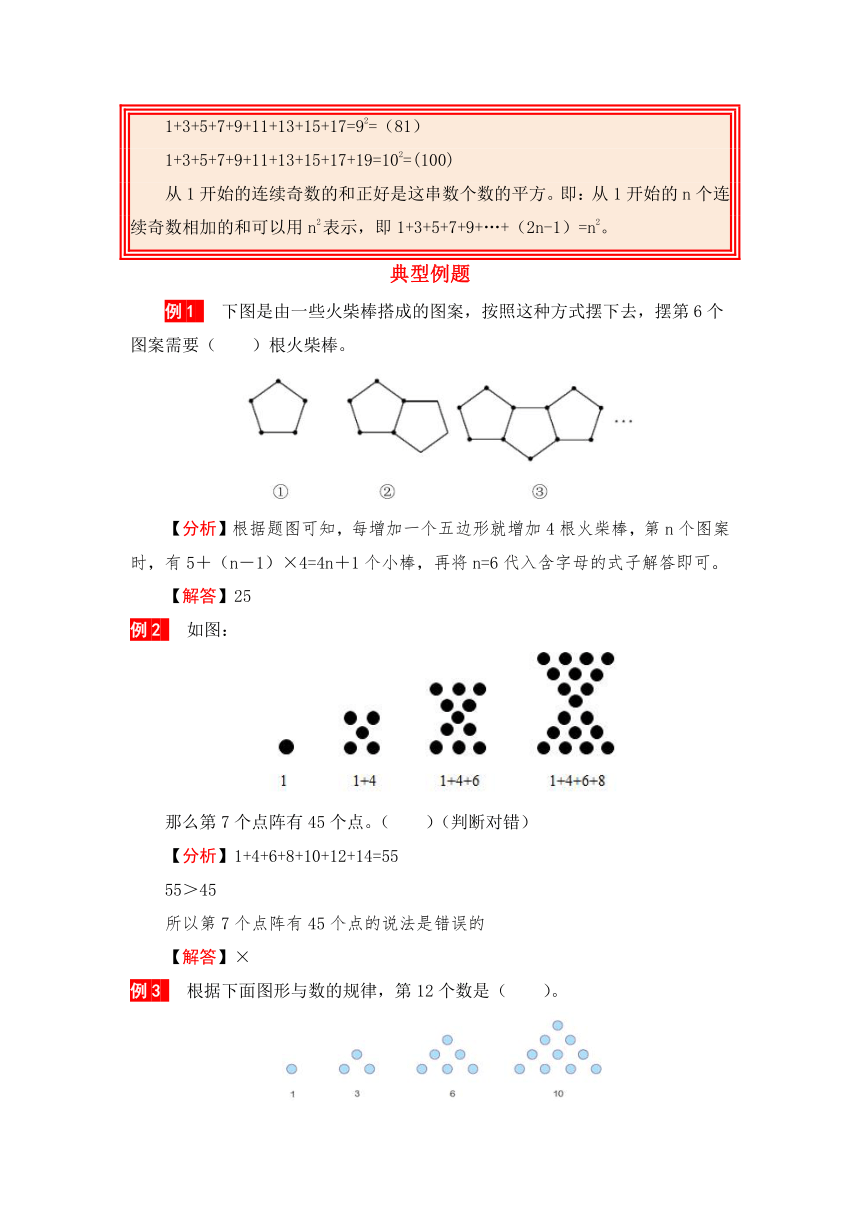
例1 下图是由一些火柴棒搭成的图案,按照这种方式摆下去,摆第6个图案需要( )根火柴棒。
【分析】根据题图可知,每增加一个五边形就增加4根火柴棒,第n个图案时,有5+(n-1)×4=4n+1个小棒,再将n=6代入含字母的式子解答即可。
【解答】25
例2 如图:
那么第7个点阵有45个点。( )(判断对错)
【分析】1+4+6+8+10+12+14=55
55>45
所以第7个点阵有45个点的说法是错误的
【解答】×
例3 根据下面图形与数的规律,第12个数是( )。
A.24 B.36 C.60 D.78
【分析】圆片的数量=1+2+3+……+n,据此分析。
1+2+3+4+5+6+7+8+9+10+11+12
=(1+12)×12÷2
=13×12÷2
=78
【解答】D
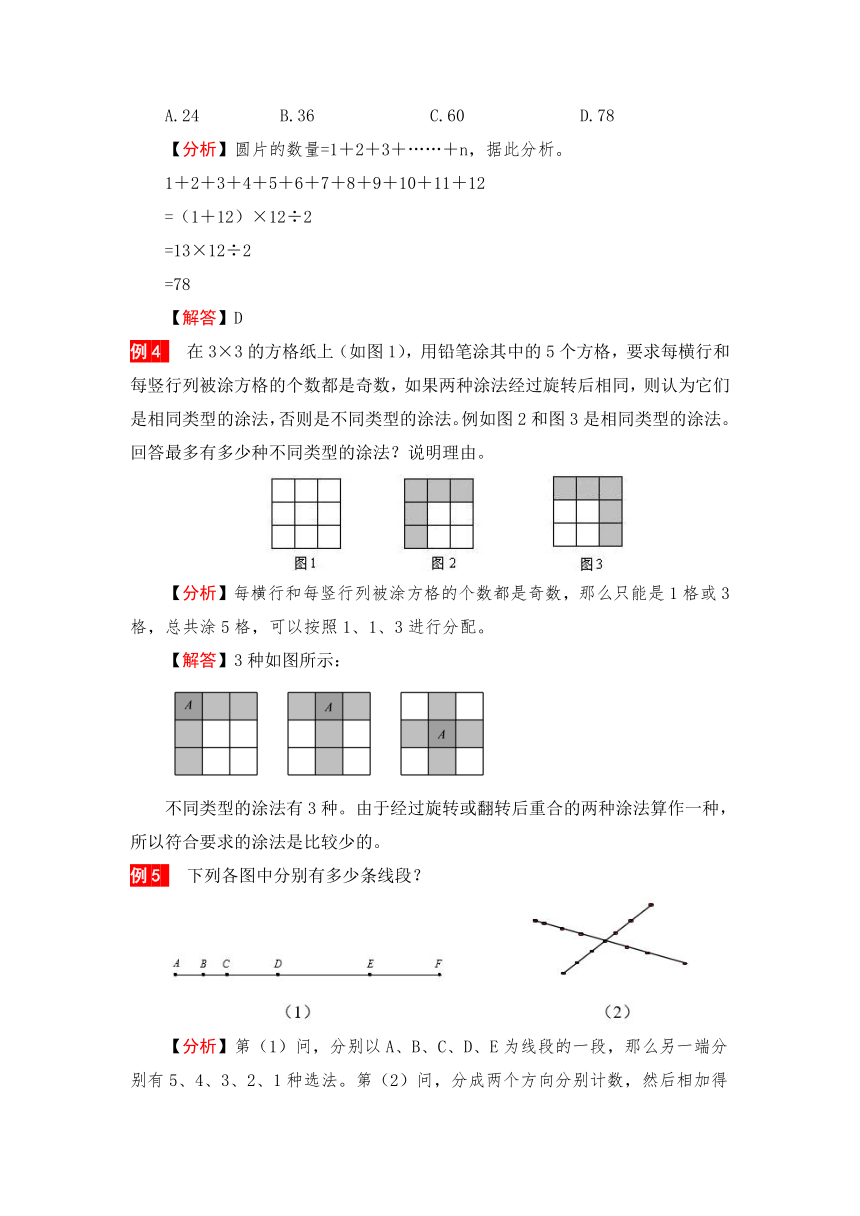
例4 在3×3的方格纸上(如图1),用铅笔涂其中的5个方格,要求每横行和每竖行列被涂方格的个数都是奇数,如果两种涂法经过旋转后相同,则认为它们是相同类型的涂法,否则是不同类型的涂法。例如图2和图3是相同类型的涂法。回答最多有多少种不同类型的涂法?说明理由。
【分析】每横行和每竖行列被涂方格的个数都是奇数,那么只能是1格或3格,总共涂5格,可以按照1、1、3进行分配。
【解答】3种如图所示:
不同类型的涂法有3种。由于经过旋转或翻转后重合的两种涂法算作一种,所以符合要求的涂法是比较少的。
例5 下列各图中分别有多少条线段?
【分析】第(1)问,分别以A、B、C、D、E为线段的一段,那么另一端分别有5、4、3、2、1种选法。第(2)问,分成两个方向分别计数,然后相加得到总数。
【解答】(1)15条 (2)49条
(1)(条)
(2)(条)
(条)
(条)
答:图(1)有15条线段,图(2)有49条线段。
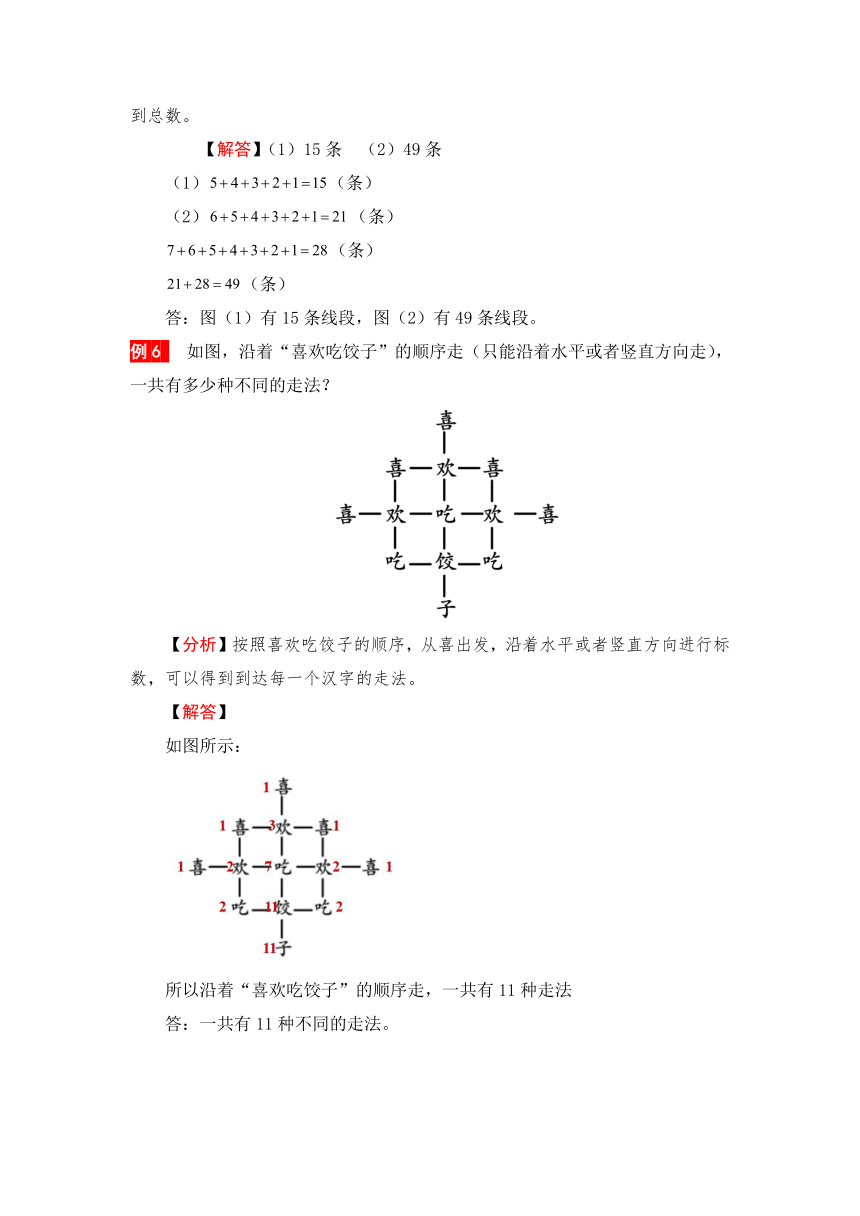
例6 如图,沿着“喜欢吃饺子”的顺序走(只能沿着水平或者竖直方向走),一共有多少种不同的走法?
【分析】按照喜欢吃饺子的顺序,从喜出发,沿着水平或者竖直方向进行标数,可以得到到达每一个汉字的走法。
【解答】
如图所示:
所以沿着“喜欢吃饺子”的顺序走,一共有11种走法
答:一共有11种不同的走法。
当堂训练
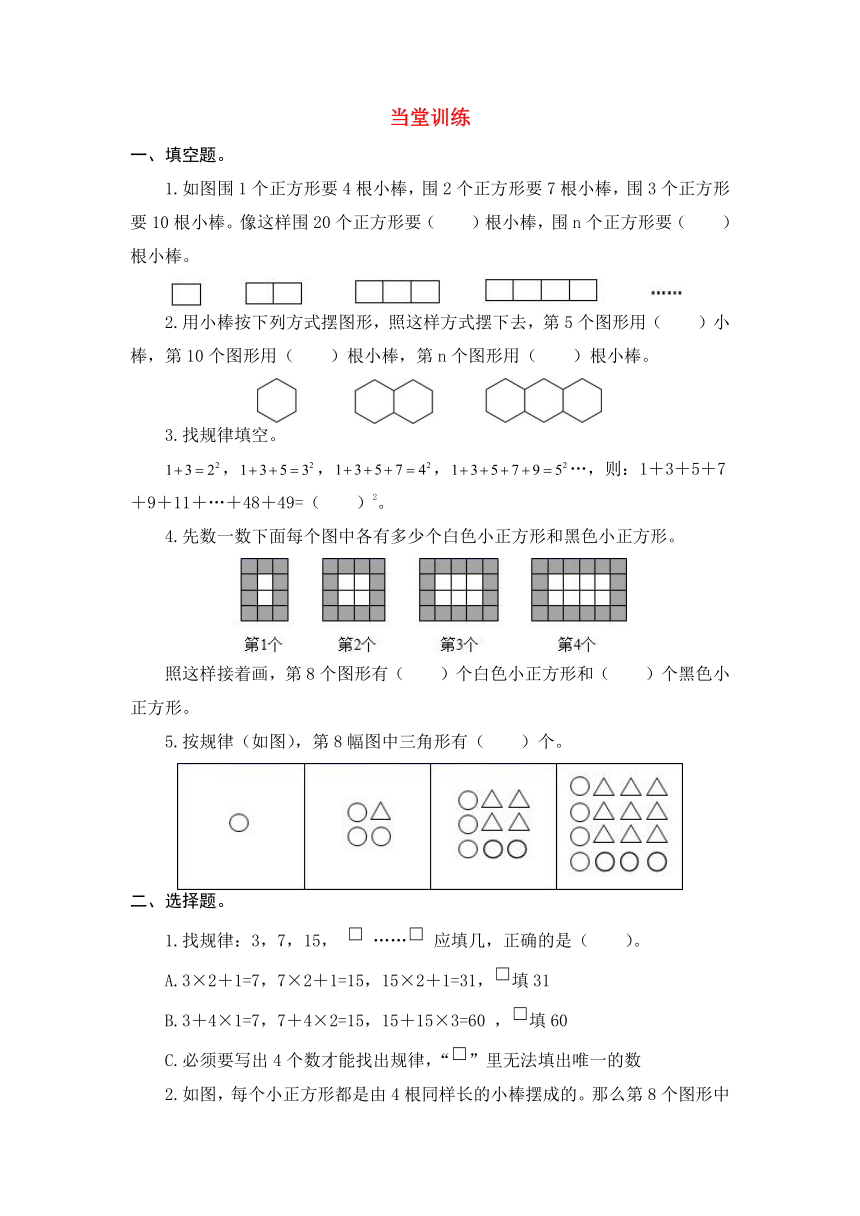
一、填空题。
1.如图围1个正方形要4根小棒,围2个正方形要7根小棒,围3个正方形要10根小棒。像这样围20个正方形要( )根小棒,围n个正方形要( )根小棒。
2.用小棒按下列方式摆图形,照这样方式摆下去,第5个图形用( )小棒,第10个图形用( )根小棒,第n个图形用( )根小棒。
3.找规律填空。
,,,…,则:1+3+5+7+9+11+…+48+49=( )2。
4.先数一数下面每个图中各有多少个白色小正方形和黑色小正方形。
照这样接着画,第8个图形有( )个白色小正方形和( )个黑色小正方形。
5.按规律(如图),第8幅图中三角形有( )个。
二、选择题。
1.找规律:3,7,15, …… 应填几,正确的是( )。
A.3×2+1=7,7×2+1=15,15×2+1=31,填31
B.3+4×1=7,7+4×2=15,15+15×3=60 ,填60
C.必须要写出4个数才能找出规律,“”里无法填出唯一的数
2.如图,每个小正方形都是由4根同样长的小棒摆成的。那么第8个图形中一共用( )根小棒。
A.324 B.144 C.160
3.数与形结合是一种重要的数学思想,认真观察下面的图形,“2020”这个数在_______个三角形的_______顶点处。应选( )。
A.673,左下 B.674,上 C.673,右下 D.674,左下
4.观察下面点阵图找规律,第8个点阵图中有( )个点。
A.27 B.25 C.28 D.26
5.用灰、白两种六边形瓷砖按如图所示的规律拼成图案,继续拼下去,第10个图案中有( )块白色瓷砖。
第1个 第2个 第3个
A.10 B.40 C.42 D.60
三、判断题。
1.观察规律:2、4、6、10、16,接下去是24。( )
2.如图这样放三角形积木,如果最下层放19块积木,共需放72块积木。( )
3.小数点后第80位上的数字是2。( )
4.8个点可以连成20条线段。( )
5.如图,第五个点阵中点的个数是17个。( )
四、解决问题。
1.辨析选优,我有主见。
1,3,6,10( )……
聪聪发现的规律是依次增加2、3、4、5……括号里填15 明明发现求第几个数就是从1连续加到几,第五个数为:1+2+3+4+5=15 你认为哪种规律较好?说一说你的理由。
2.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
3.如图,堆三角形积木。
①如果下层放6个,一共需要多少个三角形?
②如果有169个三角形积木块,下层应放几个?
4.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示,按照下面的规律摆下去。
(1)摆6个“金鱼”需要多少根火柴棒?
(2)摆n个“金鱼”需要多少根火柴棒?
(3)若有2018根火柴棒,那么可以摆多少个“金鱼”?
5.用同样长的小棒摆正方形,如图:
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 …
(1)填一填。
(2)这样摆7个正方形,需要多少根小棒?
(3)现有31根小棒,能摆多少个这样的正方形?
6.规定:如图1中,方格里的数表示在其周围8个方格中共有多少个△。即以“1”为中心,在它的四周8个方格中只能有1个△ 以“2”为中心,在它的四周8个方格中只能有2个△ 以“3”为中心,在它的四周8个方格中只能有3个△ 依此类推。
按上述规定,在如图2中一共可以画12个△。现在已经画好了其中的2个,请你在合适的空格中补上其余的10个。
参考答案
一、1.61 3n+1
2.26 51 5n+1
3.25
4.16 24
5.49
二、1.C 2.B 3.B 4.A 5.C
三、1.× 2.× 3.√ 4.× 5.√
四、1.1=1=
1+2=3=
1+2+3=6=
故1+2+3+…+n=
所以对于较大的数,相比明明发现的规律更好计算。
答:我认为明明发现的规律较好,对于较大的数更好计算。
2.(1)分析图形规律可知:
第n个图形小正方形的总个数:3(n+2)=3n+6
第n个图形黑色小正方形的个数:n个
第n个图形白色小正方形的个数:3n+6-n=2n+6
当n=10时,
白色小正方形的个数:2n+6=2×10+6=26(个)
黑色小正方形的个数:10个
答:第10个图形中白色小正方形有26个,黑色小正方形有10个。
(2)由题意可知,
2n+6=38
解:2n=38-6
2n=32
n=32÷2
n=16
答:如果某个图形中有38个白色小正方形,那么这个图形排在第16。
3.①6×6=36个
答:如果下层放6个,一共需要36个三角形。
②13×13=169
答:如果有169个三角形积木块,下层应放了13个。
4.(1)8+(6-1)×6
=8+5×6
=8+30
=38(根)
答:摆6个“金鱼”需要38根火柴棒。
(2)摆n条“金鱼”需用火柴棒的根数为8+(n-1)×6根
(3)(2018-8)÷6+1
=2010÷6+1
=335+1
=336(个)
答:2018根火柴棒可以摆336个“金鱼”。
5.(1)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 13 16 …
4个正方形小棒根数:1+3×4=13(根)
5个正方形小棒根数:1+3×5=16(根)
(2)1+3×7=22(根)
答:摆7个正方形,需要22根小棒。
(3)解:设31根小棒,能摆n个这样的正方形。
1+3n=31
3n=31-1
3n=30
n=30÷3
n=10
答:31根小棒,能摆10个这样的正方形。
6.如图:
第八单元 数学广角——数与形
单元知识要点
通过自主探究发现图形中隐藏着的数的规律,并体会运用发现的规律解决问题的简捷性。能利用数形结合思想来解决一些与数有关的问题。体会数结合思想的重要性,训练思维的灵活性和准确性。
知识点归纳总结
1.2+4+6+8+10+12+14+16+18+20=(110)
规律∶从 2开始的 n个连续偶数的和等于n×(n+1)。
10×(10+1)=10×11=110
2.1=12=1
1+3=22=(4)
1+3+5=32=(9)
1+3+5+7=42=(16)
1+3+5+7+9=52=(25)
1+3+5+7+9+11=62=(36)
1+3+5+7+9+11+13=72=(49)
1+3+5+7+9+11+13+15=82=(64)
1+3+5+7+9+11+13+15+17=92=(81)
1+3+5+7+9+11+13+15+17+19=102=(100)
从1开始的连续奇数的和正好是这串数个数的平方。即:从1开始的n个连续奇数相加的和可以用n2表示,即1+3+5+7+9+…+(2n-1)=n2。
典型例题
例1 下图是由一些火柴棒搭成的图案,按照这种方式摆下去,摆第6个图案需要( )根火柴棒。
【分析】根据题图可知,每增加一个五边形就增加4根火柴棒,第n个图案时,有5+(n-1)×4=4n+1个小棒,再将n=6代入含字母的式子解答即可。
【解答】25
例2 如图:
那么第7个点阵有45个点。( )(判断对错)
【分析】1+4+6+8+10+12+14=55
55>45
所以第7个点阵有45个点的说法是错误的
【解答】×
例3 根据下面图形与数的规律,第12个数是( )。
A.24 B.36 C.60 D.78
【分析】圆片的数量=1+2+3+……+n,据此分析。
1+2+3+4+5+6+7+8+9+10+11+12
=(1+12)×12÷2
=13×12÷2
=78
【解答】D
例4 在3×3的方格纸上(如图1),用铅笔涂其中的5个方格,要求每横行和每竖行列被涂方格的个数都是奇数,如果两种涂法经过旋转后相同,则认为它们是相同类型的涂法,否则是不同类型的涂法。例如图2和图3是相同类型的涂法。回答最多有多少种不同类型的涂法?说明理由。
【分析】每横行和每竖行列被涂方格的个数都是奇数,那么只能是1格或3格,总共涂5格,可以按照1、1、3进行分配。
【解答】3种如图所示:
不同类型的涂法有3种。由于经过旋转或翻转后重合的两种涂法算作一种,所以符合要求的涂法是比较少的。
例5 下列各图中分别有多少条线段?
【分析】第(1)问,分别以A、B、C、D、E为线段的一段,那么另一端分别有5、4、3、2、1种选法。第(2)问,分成两个方向分别计数,然后相加得到总数。
【解答】(1)15条 (2)49条
(1)(条)
(2)(条)
(条)
(条)
答:图(1)有15条线段,图(2)有49条线段。
例6 如图,沿着“喜欢吃饺子”的顺序走(只能沿着水平或者竖直方向走),一共有多少种不同的走法?
【分析】按照喜欢吃饺子的顺序,从喜出发,沿着水平或者竖直方向进行标数,可以得到到达每一个汉字的走法。
【解答】
如图所示:
所以沿着“喜欢吃饺子”的顺序走,一共有11种走法
答:一共有11种不同的走法。
当堂训练
一、填空题。
1.如图围1个正方形要4根小棒,围2个正方形要7根小棒,围3个正方形要10根小棒。像这样围20个正方形要( )根小棒,围n个正方形要( )根小棒。
2.用小棒按下列方式摆图形,照这样方式摆下去,第5个图形用( )小棒,第10个图形用( )根小棒,第n个图形用( )根小棒。
3.找规律填空。
,,,…,则:1+3+5+7+9+11+…+48+49=( )2。
4.先数一数下面每个图中各有多少个白色小正方形和黑色小正方形。
照这样接着画,第8个图形有( )个白色小正方形和( )个黑色小正方形。
5.按规律(如图),第8幅图中三角形有( )个。
二、选择题。
1.找规律:3,7,15, …… 应填几,正确的是( )。
A.3×2+1=7,7×2+1=15,15×2+1=31,填31
B.3+4×1=7,7+4×2=15,15+15×3=60 ,填60
C.必须要写出4个数才能找出规律,“”里无法填出唯一的数
2.如图,每个小正方形都是由4根同样长的小棒摆成的。那么第8个图形中一共用( )根小棒。
A.324 B.144 C.160
3.数与形结合是一种重要的数学思想,认真观察下面的图形,“2020”这个数在_______个三角形的_______顶点处。应选( )。
A.673,左下 B.674,上 C.673,右下 D.674,左下
4.观察下面点阵图找规律,第8个点阵图中有( )个点。
A.27 B.25 C.28 D.26
5.用灰、白两种六边形瓷砖按如图所示的规律拼成图案,继续拼下去,第10个图案中有( )块白色瓷砖。
第1个 第2个 第3个
A.10 B.40 C.42 D.60
三、判断题。
1.观察规律:2、4、6、10、16,接下去是24。( )
2.如图这样放三角形积木,如果最下层放19块积木,共需放72块积木。( )
3.小数点后第80位上的数字是2。( )
4.8个点可以连成20条线段。( )
5.如图,第五个点阵中点的个数是17个。( )
四、解决问题。
1.辨析选优,我有主见。
1,3,6,10( )……
聪聪发现的规律是依次增加2、3、4、5……括号里填15 明明发现求第几个数就是从1连续加到几,第五个数为:1+2+3+4+5=15 你认为哪种规律较好?说一说你的理由。
2.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
3.如图,堆三角形积木。
①如果下层放6个,一共需要多少个三角形?
②如果有169个三角形积木块,下层应放几个?
4.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示,按照下面的规律摆下去。
(1)摆6个“金鱼”需要多少根火柴棒?
(2)摆n个“金鱼”需要多少根火柴棒?
(3)若有2018根火柴棒,那么可以摆多少个“金鱼”?
5.用同样长的小棒摆正方形,如图:
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 …
(1)填一填。
(2)这样摆7个正方形,需要多少根小棒?
(3)现有31根小棒,能摆多少个这样的正方形?
6.规定:如图1中,方格里的数表示在其周围8个方格中共有多少个△。即以“1”为中心,在它的四周8个方格中只能有1个△ 以“2”为中心,在它的四周8个方格中只能有2个△ 以“3”为中心,在它的四周8个方格中只能有3个△ 依此类推。
按上述规定,在如图2中一共可以画12个△。现在已经画好了其中的2个,请你在合适的空格中补上其余的10个。
参考答案
一、1.61 3n+1
2.26 51 5n+1
3.25
4.16 24
5.49
二、1.C 2.B 3.B 4.A 5.C
三、1.× 2.× 3.√ 4.× 5.√
四、1.1=1=
1+2=3=
1+2+3=6=
故1+2+3+…+n=
所以对于较大的数,相比明明发现的规律更好计算。
答:我认为明明发现的规律较好,对于较大的数更好计算。
2.(1)分析图形规律可知:
第n个图形小正方形的总个数:3(n+2)=3n+6
第n个图形黑色小正方形的个数:n个
第n个图形白色小正方形的个数:3n+6-n=2n+6
当n=10时,
白色小正方形的个数:2n+6=2×10+6=26(个)
黑色小正方形的个数:10个
答:第10个图形中白色小正方形有26个,黑色小正方形有10个。
(2)由题意可知,
2n+6=38
解:2n=38-6
2n=32
n=32÷2
n=16
答:如果某个图形中有38个白色小正方形,那么这个图形排在第16。
3.①6×6=36个
答:如果下层放6个,一共需要36个三角形。
②13×13=169
答:如果有169个三角形积木块,下层应放了13个。
4.(1)8+(6-1)×6
=8+5×6
=8+30
=38(根)
答:摆6个“金鱼”需要38根火柴棒。
(2)摆n条“金鱼”需用火柴棒的根数为8+(n-1)×6根
(3)(2018-8)÷6+1
=2010÷6+1
=335+1
=336(个)
答:2018根火柴棒可以摆336个“金鱼”。
5.(1)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 13 16 …
4个正方形小棒根数:1+3×4=13(根)
5个正方形小棒根数:1+3×5=16(根)
(2)1+3×7=22(根)
答:摆7个正方形,需要22根小棒。
(3)解:设31根小棒,能摆n个这样的正方形。
1+3n=31
3n=31-1
3n=30
n=30÷3
n=10
答:31根小棒,能摆10个这样的正方形。
6.如图:
