27.3 位似 课件(共22张PPT)2022-2023学年人教版九年级数学下册
文档属性
| 名称 | 27.3 位似 课件(共22张PPT)2022-2023学年人教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 828.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 20:06:39 | ||
图片预览



文档简介
(共22张PPT)
(1)理解位似图形的概念,掌握位似图形的性质;
(2)利用位似图形的性质,掌握作位似图形的方法,并对图形放大或缩小.
重点:了解位似图形的概念、性质
难点:利用位似将一个图形放大或缩小
教学目标
重点难点
位似
人教版数学九年级下册第二十七章《相似三角形》
九年级数学备课组
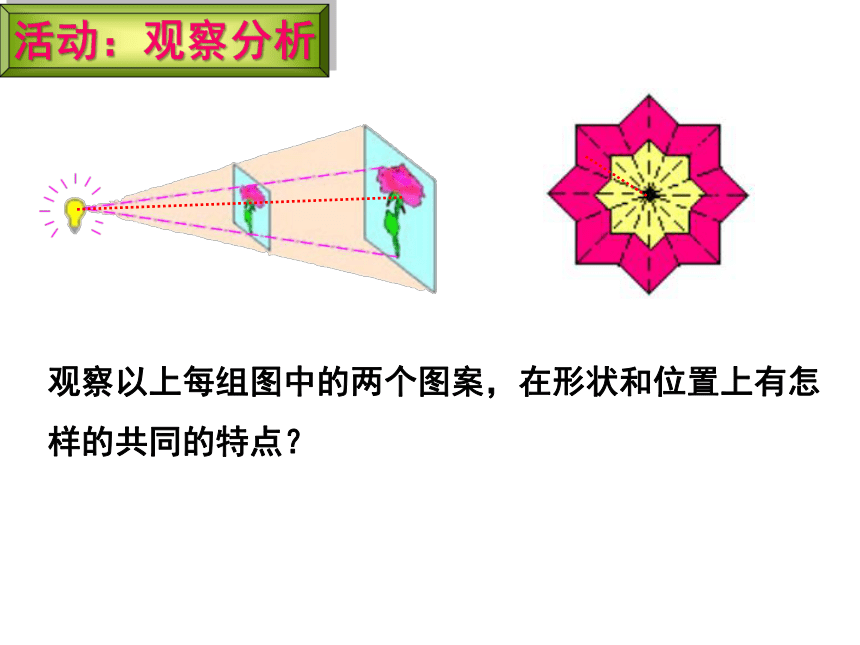
观察以上每组图中的两个图案,在形状和位置上有怎样的共同的特点?
活动:观察分析
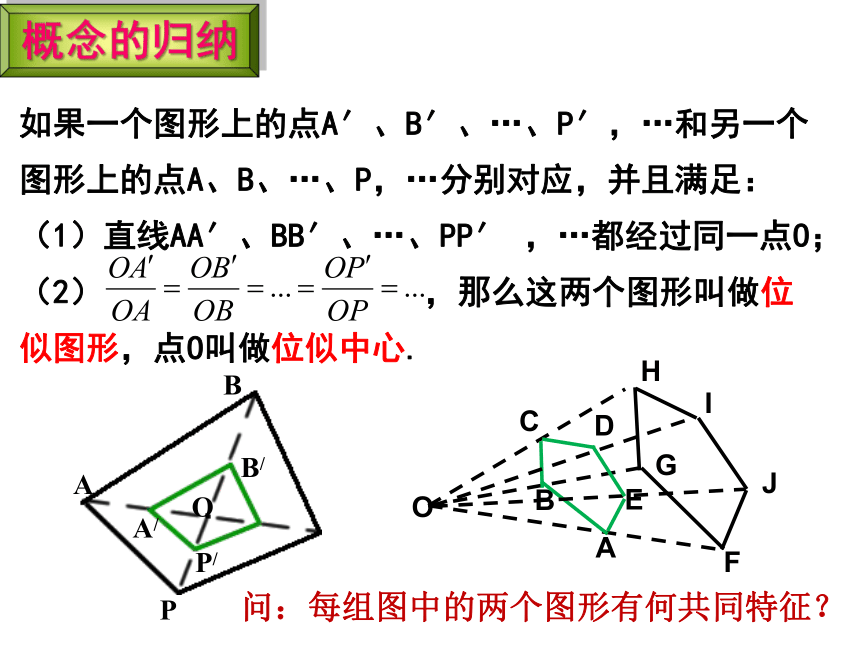
如果一个图形上的点A′、B′、…、P′,…和另一个图形上的点A、B、…、P,…分别对应,并且满足:
(1)直线AA′、BB′、…、PP′ ,…都经过同一点O;
(2) ,那么这两个图形叫做位似图形,点O叫做位似中心.
概念的归纳
F
H
E
A
O
C
B
D
G
I
J
P
P/
B
B/
A
A/
O
问:每组图中的两个图形有何共同特征?
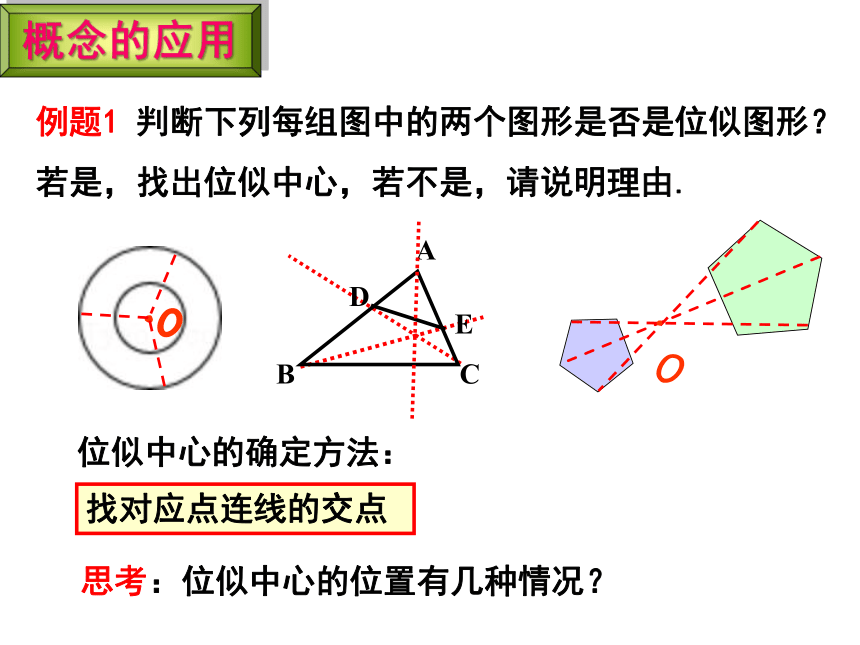
例题1 判断下列每组图中的两个图形是否是位似图形?若是,找出位似中心,若不是,请说明理由.
概念的应用
位似中心的确定方法:
·
O
找对应点连线的交点
思考:位似中心的位置有几种情况?
·o
A
B
C
D
E
活动:思考分析
位似图形和相似图形有什么区别和联系?
答:位似图形一定相似,
相似图形不一定位似.
位似图形:
性质:对应点连线交于一点,位似中心到对应点的距离之比相等;
结论:1.对应边平行或共线;2.位似中心到对应点的距离之比等于相似比.
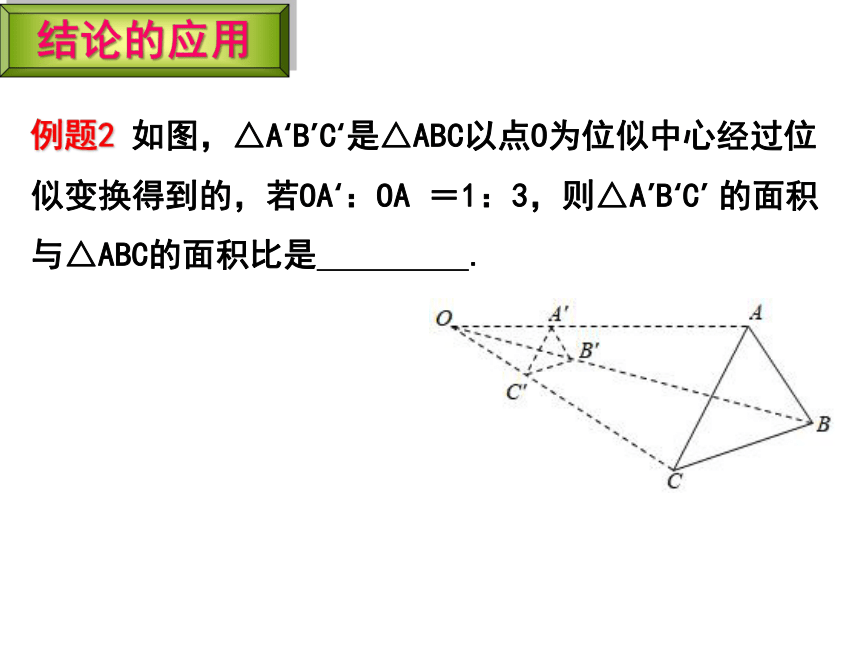
例题2 如图,△A‘B’C‘是△ABC以点O为位似中心经过位似变换得到的,若OA‘:OA =1:3,则△A’B‘C’ 的面积与△ABC的面积比是 .
结论的应用
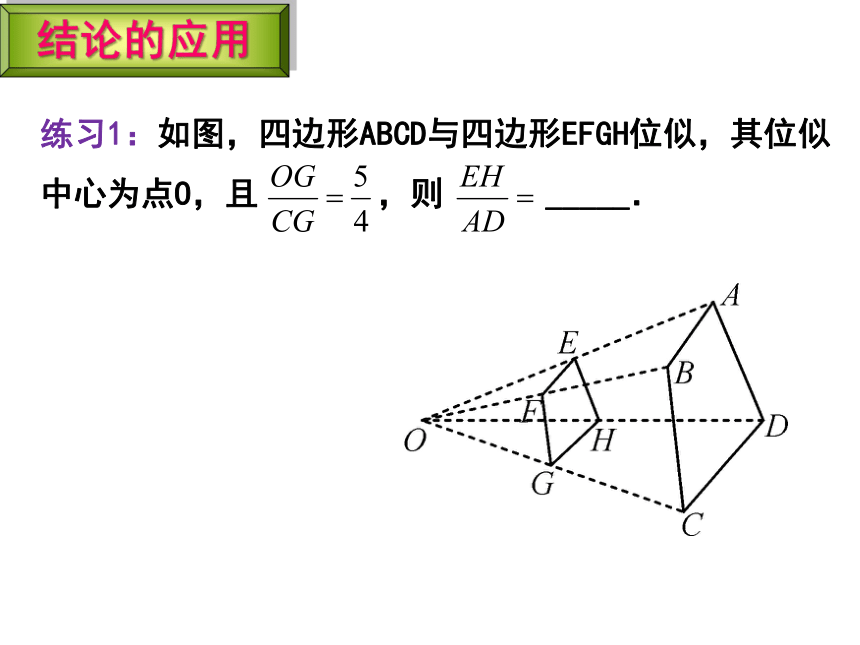
练习1:如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 _____.
结论的应用
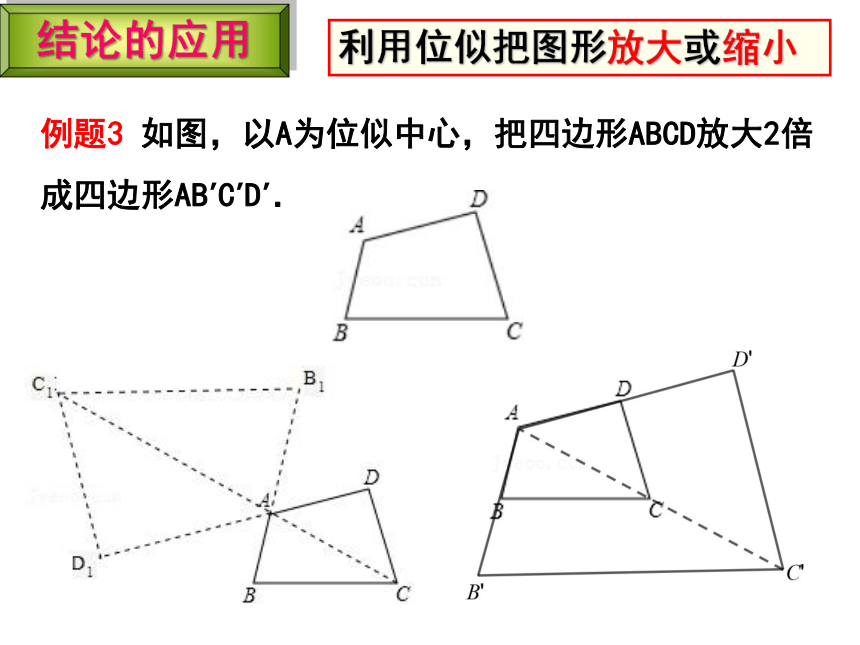
例题3 如图,以A为位似中心,把四边形ABCD放大2倍成四边形AB’C’D’.
结论的应用
利用位似把图形放大或缩小
法一:如图,在△ABC外任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;
O
A
B
C
F
●
E
●
D
●
利用位似把图形放大或缩小
结论的应用
练习3 如何将△ABC按比例缩小为原来的 ?
顺次连接D,E,F,△DEF即为所求.
F
●
法二:如图,在△ABC外任取一点O,分别在AO,BO,CO的延长线上取点D,E,F,使得
A
B
C
●
E
D
●
利用位似把图形放大或缩小
例题3 如何将△ABC按比例缩小为原来的 ?
O
△DEF即为所求.
结论的应用
利用位似把图形放大或缩小
如何将△ABC按比例缩小为原来的 .
F
●
A
B
C
●
E
D
●
O
O
A
B
C
F
●
E
●
D
●
图形在位似中心同侧
图形在位似中心异侧
结论的应用
知识回顾
1、位似的两个图形有怎样的性质?
2、找出下列位似图形的位似中心O,并说出相似比.
O
A
B
C
F
●
E
●
D
●
位似比
(2)△DEF∽△ABC
相似比=位似比
A
B
C
H
G
M
O
1.在坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,把线段AB缩小为A‘B’,相似比为,说出对应点坐标.
B'
A'
x
y
B(6,0)
A(6,3)
o
问题探究
(2,1)
(2,0)
思考:还有其他作图方法吗?
B'
A'
x
y
B(6,0)
A(6,3)
o
(2,1)
(2,0)
A”
B”
(-2,0)
(-2,-1)
观察对应点之间的坐标的变化,你有什么发现
问题探究
1.在坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,把线段AB缩小为A‘B’,相似比为,说出对应点坐标.
2.如图,△AOC的三个顶点的坐标分别为A(4,4),0(0,0),C(5,0),以原点O为位似中心,将△AOC放大为△A’OC’,使它与△AOC的相似比为2,直接说出对应点的坐标.
C'
A'
x
y
C(5,0)
o
(8,8)
(10,0)
A(4,4)
?
问题探究
A'(8,8)或(-8,-8)
C'(10,0)或(-10,0)
结论归纳
一般地,在直角坐标系中,如果两个位似图形以原点为位似中心,且与原图形的相似比为k,那么原图形上点(x,y)对应点的坐标为__________或____________.
(kx,ky)
(-kx,-ky)
同侧
异侧
P’(kx, ky)
P(x,y)
O
x
y
P’’(-kx, -ky)
从k的大小你能判断是将原图形放大还是缩小吗?
例1 已知△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0),以原点O为位似中心,△A’B’O的与△ABO的位似比为,求A’、B’的坐标.
结论应用
练习1:课本p50练习1,练习2
根据相似比判断:这是放大?还是缩小?
练习2:以原点O为位似中心,将△ABO进行位似变换,得到对应△A’B’O’,已知A(6,3), B(4,-5) ,A’(-2,-1),则△A’B’O’和△ABO的相似比为 ,B’的坐标为 .
结论应用
例2 在平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3),△AB’O’是△ABO以点A为位似中心的位似图形,且O’的坐标为(1,0),则点B’的坐标为________.
A
B
O
x
y
拓展提升
练习3:课本p52第7题
课堂小结
今天你学到了什么?从知识和思想方法两个方面说明.
作业:加油站p35-36
对比位似和平移、旋转、轴对称,它们有什么区别和联系.
拓展提升
(1)理解位似图形的概念,掌握位似图形的性质;
(2)利用位似图形的性质,掌握作位似图形的方法,并对图形放大或缩小.
重点:了解位似图形的概念、性质
难点:利用位似将一个图形放大或缩小
教学目标
重点难点
位似
人教版数学九年级下册第二十七章《相似三角形》
九年级数学备课组
观察以上每组图中的两个图案,在形状和位置上有怎样的共同的特点?
活动:观察分析
如果一个图形上的点A′、B′、…、P′,…和另一个图形上的点A、B、…、P,…分别对应,并且满足:
(1)直线AA′、BB′、…、PP′ ,…都经过同一点O;
(2) ,那么这两个图形叫做位似图形,点O叫做位似中心.
概念的归纳
F
H
E
A
O
C
B
D
G
I
J
P
P/
B
B/
A
A/
O
问:每组图中的两个图形有何共同特征?
例题1 判断下列每组图中的两个图形是否是位似图形?若是,找出位似中心,若不是,请说明理由.
概念的应用
位似中心的确定方法:
·
O
找对应点连线的交点
思考:位似中心的位置有几种情况?
·o
A
B
C
D
E
活动:思考分析
位似图形和相似图形有什么区别和联系?
答:位似图形一定相似,
相似图形不一定位似.
位似图形:
性质:对应点连线交于一点,位似中心到对应点的距离之比相等;
结论:1.对应边平行或共线;2.位似中心到对应点的距离之比等于相似比.
例题2 如图,△A‘B’C‘是△ABC以点O为位似中心经过位似变换得到的,若OA‘:OA =1:3,则△A’B‘C’ 的面积与△ABC的面积比是 .
结论的应用
练习1:如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 _____.
结论的应用
例题3 如图,以A为位似中心,把四边形ABCD放大2倍成四边形AB’C’D’.
结论的应用
利用位似把图形放大或缩小
法一:如图,在△ABC外任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;
O
A
B
C
F
●
E
●
D
●
利用位似把图形放大或缩小
结论的应用
练习3 如何将△ABC按比例缩小为原来的 ?
顺次连接D,E,F,△DEF即为所求.
F
●
法二:如图,在△ABC外任取一点O,分别在AO,BO,CO的延长线上取点D,E,F,使得
A
B
C
●
E
D
●
利用位似把图形放大或缩小
例题3 如何将△ABC按比例缩小为原来的 ?
O
△DEF即为所求.
结论的应用
利用位似把图形放大或缩小
如何将△ABC按比例缩小为原来的 .
F
●
A
B
C
●
E
D
●
O
O
A
B
C
F
●
E
●
D
●
图形在位似中心同侧
图形在位似中心异侧
结论的应用
知识回顾
1、位似的两个图形有怎样的性质?
2、找出下列位似图形的位似中心O,并说出相似比.
O
A
B
C
F
●
E
●
D
●
位似比
(2)△DEF∽△ABC
相似比=位似比
A
B
C
H
G
M
O
1.在坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,把线段AB缩小为A‘B’,相似比为,说出对应点坐标.
B'
A'
x
y
B(6,0)
A(6,3)
o
问题探究
(2,1)
(2,0)
思考:还有其他作图方法吗?
B'
A'
x
y
B(6,0)
A(6,3)
o
(2,1)
(2,0)
A”
B”
(-2,0)
(-2,-1)
观察对应点之间的坐标的变化,你有什么发现
问题探究
1.在坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,把线段AB缩小为A‘B’,相似比为,说出对应点坐标.
2.如图,△AOC的三个顶点的坐标分别为A(4,4),0(0,0),C(5,0),以原点O为位似中心,将△AOC放大为△A’OC’,使它与△AOC的相似比为2,直接说出对应点的坐标.
C'
A'
x
y
C(5,0)
o
(8,8)
(10,0)
A(4,4)
?
问题探究
A'(8,8)或(-8,-8)
C'(10,0)或(-10,0)
结论归纳
一般地,在直角坐标系中,如果两个位似图形以原点为位似中心,且与原图形的相似比为k,那么原图形上点(x,y)对应点的坐标为__________或____________.
(kx,ky)
(-kx,-ky)
同侧
异侧
P’(kx, ky)
P(x,y)
O
x
y
P’’(-kx, -ky)
从k的大小你能判断是将原图形放大还是缩小吗?
例1 已知△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0),以原点O为位似中心,△A’B’O的与△ABO的位似比为,求A’、B’的坐标.
结论应用
练习1:课本p50练习1,练习2
根据相似比判断:这是放大?还是缩小?
练习2:以原点O为位似中心,将△ABO进行位似变换,得到对应△A’B’O’,已知A(6,3), B(4,-5) ,A’(-2,-1),则△A’B’O’和△ABO的相似比为 ,B’的坐标为 .
结论应用
例2 在平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3),△AB’O’是△ABO以点A为位似中心的位似图形,且O’的坐标为(1,0),则点B’的坐标为________.
A
B
O
x
y
拓展提升
练习3:课本p52第7题
课堂小结
今天你学到了什么?从知识和思想方法两个方面说明.
作业:加油站p35-36
对比位似和平移、旋转、轴对称,它们有什么区别和联系.
拓展提升
