27.2.1 平行线分线段成比例定理 课件(共22张PPT)人教版九年级数学下册
文档属性
| 名称 | 27.2.1 平行线分线段成比例定理 课件(共22张PPT)人教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 372.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-03 21:05:33 | ||
图片预览

文档简介
(共22张PPT)
平行线分线段成比例
人教版数学九年级下册第二十七章《相似三角形》
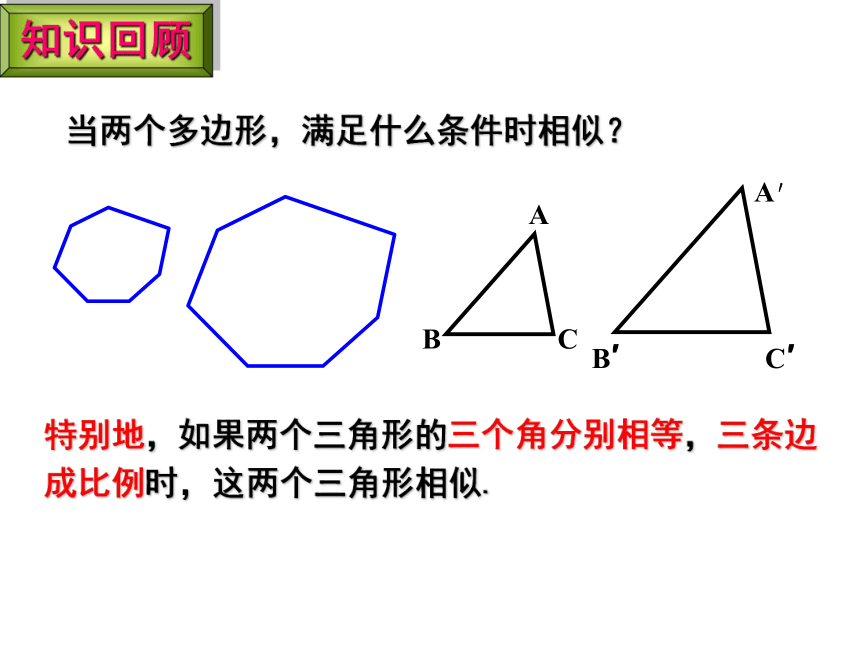
特别地,如果两个三角形的三个角分别相等,三条边成比例时,这两个三角形相似.
知识回顾
当两个多边形,满足什么条件时相似?
A
C′
B′
A′
C
B
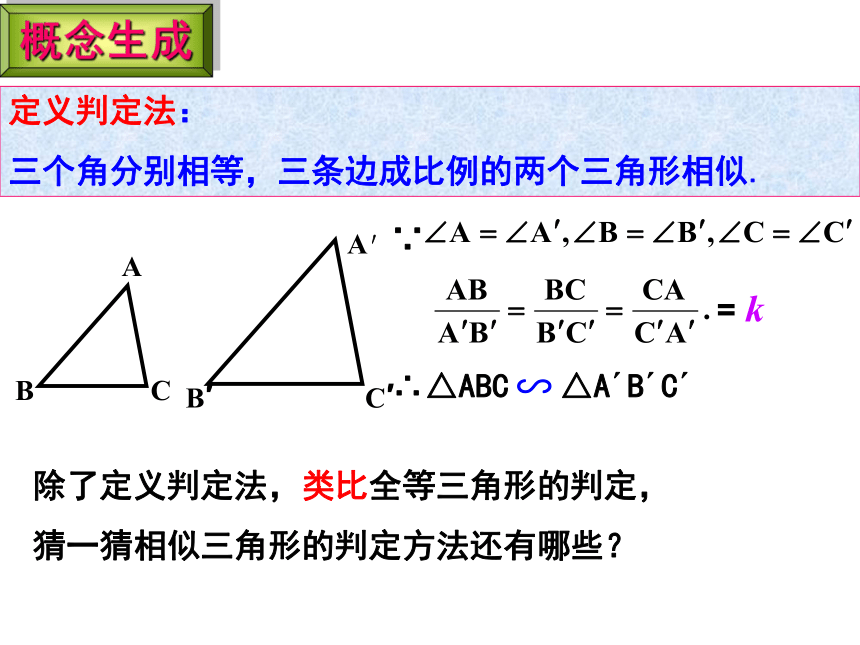
定义判定法:
三个角分别相等,三条边成比例的两个三角形相似.
除了定义判定法,类比全等三角形的判定,
猜一猜相似三角形的判定方法还有哪些?
A
C′
B′
A′
C
B
= k
∴△ABC △A B C
∵
∽
概念生成
A
E
B
C
F
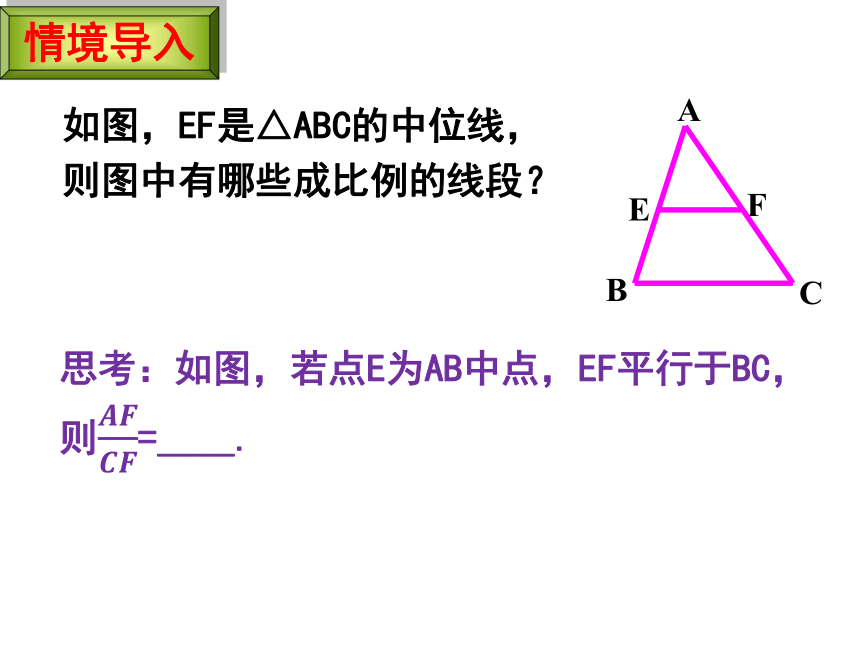
思考:如图,若点E为AB中点,EF平行于BC,则=____.
情境导入
如图,EF是△ABC的中位线,则图中有哪些成比例的线段?
A
B
C
D
E
F
l1
l2
l3
a
b
探究活动1
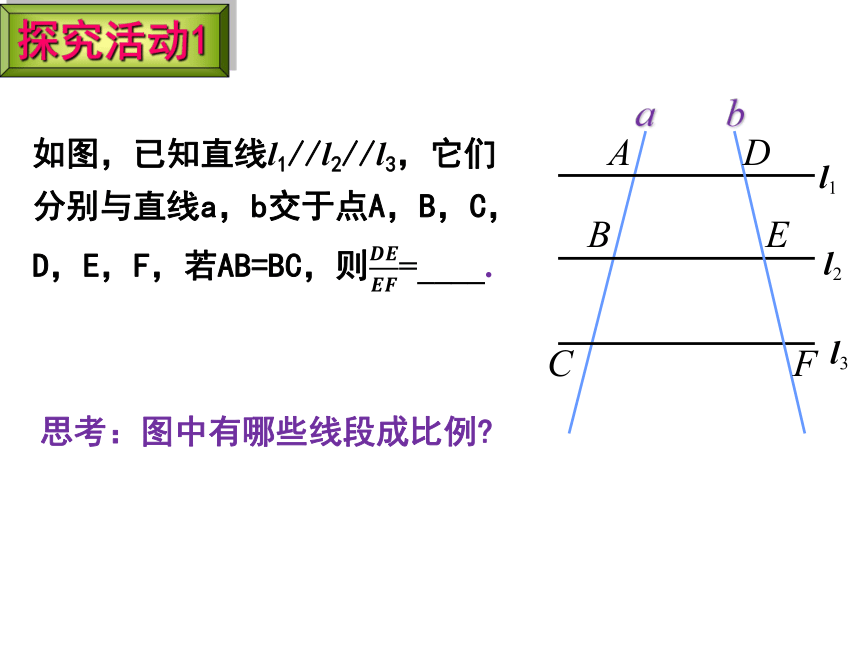
如图,已知直线l1//l2//l3,它们分别与直线a,b交于点A,B,C,D,E,F,若AB=BC,则=____.
思考:图中有哪些线段成比例
A
B
C
D
E
F
l1
l2
l3
a
b
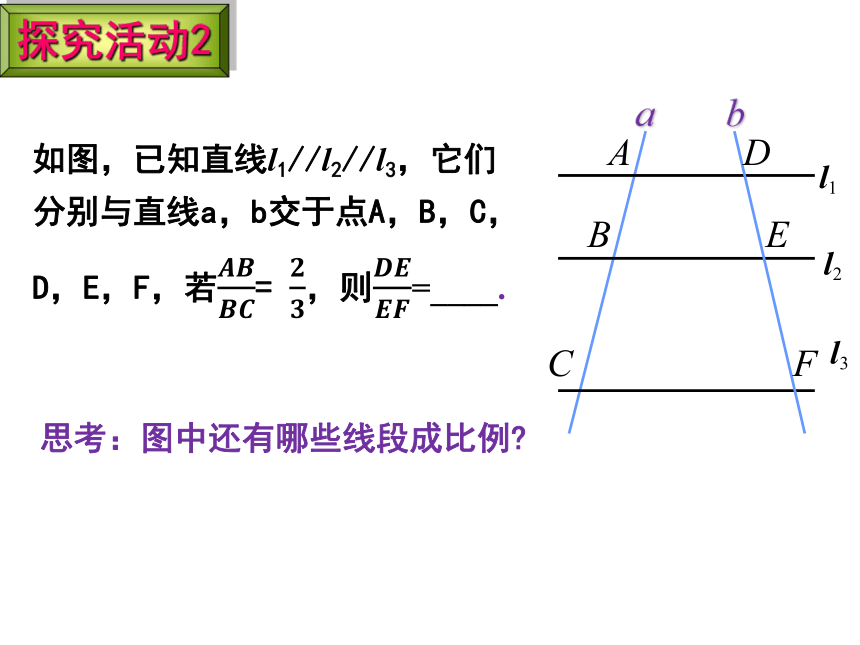
探究活动2
如图,已知直线l1//l2//l3,它们分别与直线a,b交于点A,B,C,D,E,F,若= ,则=____.
思考:图中还有哪些线段成比例
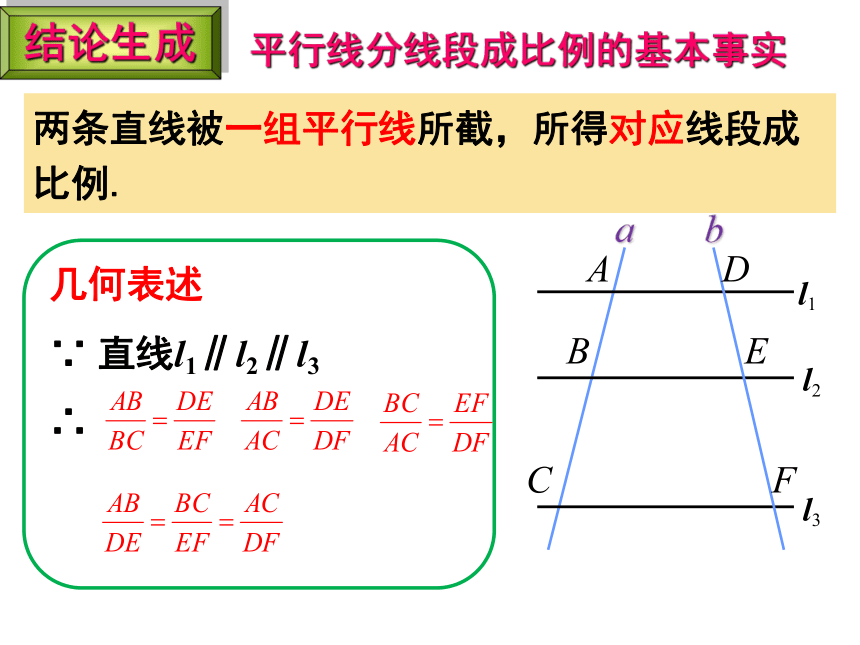
结论生成
两条直线被一组平行线所截,所得对应线段成比例.
几何表述
∵ 直线l1∥l2∥l3
∴
A
B
C
D
E
F
l1
l2
l3
a
b
平行线分线段成比例的基本事实
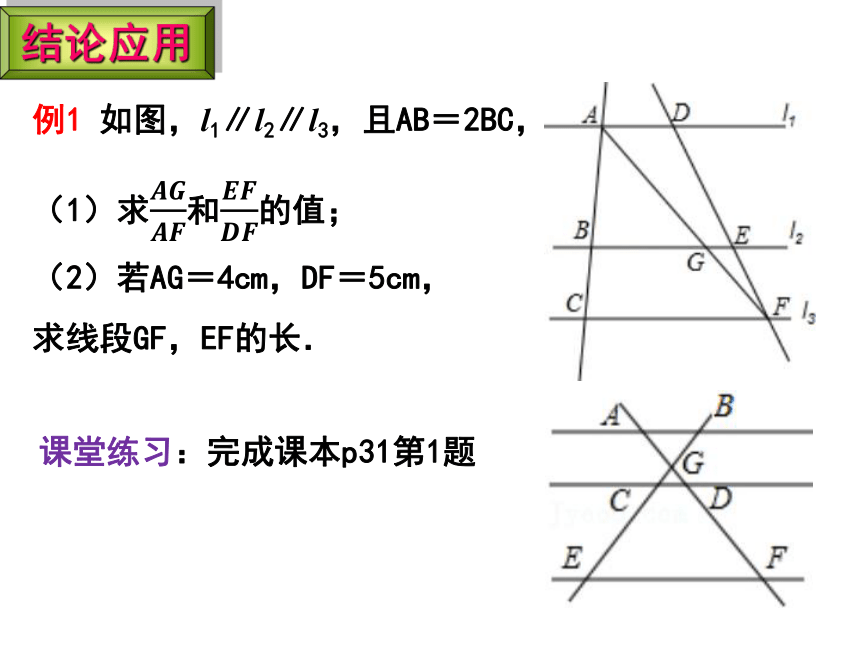
例1 如图,l1∥l2∥l3,且AB=2BC,
(1)求和的值;
(2)若AG=4cm,DF=5cm,
求线段GF,EF的长.
结论应用
课堂练习:完成课本p31第1题
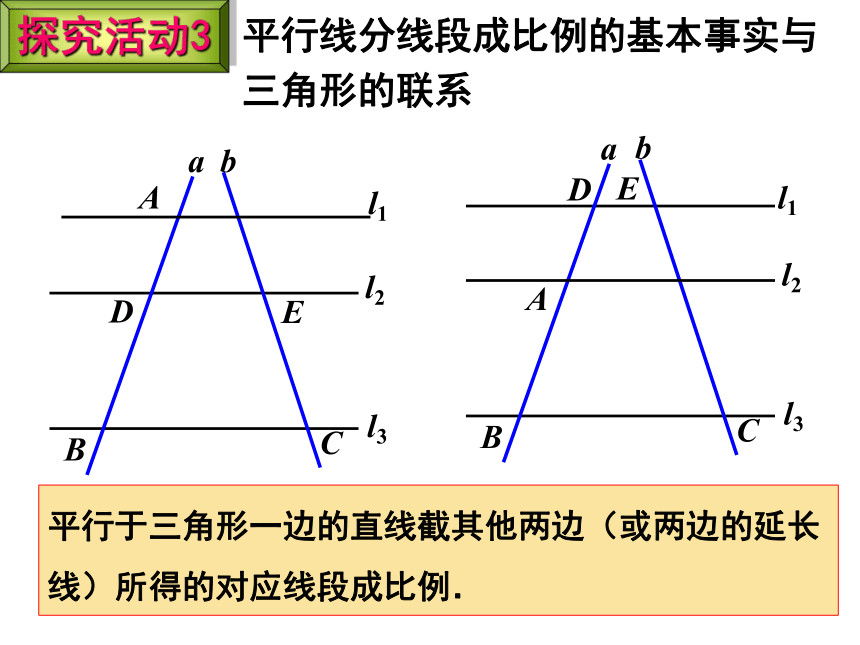
探究活动3
平行线分线段成比例的基本事实与三角形的联系
a
A
D
B
b
E
C
l1
l2
l3
a
D
A
B
b
E
C
l1
l2
l3
思考:平行于△ABC的边BC的直线,分别交直线AB、BC于D、E两点,可以得到哪些相等的线段比?
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
例2 如图,在△ABC中,DE//BC,且AD=3,DB=2,求的值.
结论应用
思考:你能求出的值吗?
类比:在△ABC中,DE//BC,
求证:= = .
F
三对角相等
△AED∽△ACB
“A”型
“8”型
(图2)
D
E
A
B
C
A
B
C
D
E
(图1)
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
结论生成
相似三角形的平行判定定理
几何表述?
例3 如图,在△ABC中,DE//BC,F在BC边上,连接AF交ED于点G,
(1)图中共有几对相似三角形?
(2)写出所有与相等的线段比.
结论应用
F
G
练习2:如图,AD∥EG∥BC,EG分别交AB、DB、AC于点E、F、G,
(1)图中有几对相似三角形,请都写出来;
(2)若AD=6,BC=10,AE=3,AB=5,求EG、FG的长.
结论应用
归纳:求线段的长,找线段所在的三角形,及与之相似的三角形,对应边成比例!
课堂小结
今天你学到了什么?从知识和思想方法两个方面说明.
作业:加油站p19,+p20第9,12,13题
(1)在横格纸上画直线l1,使得l1与横线垂直,观察直线l1被各条横线所截的线段之间有怎样的关系?
(2)再任意画一条直线l2,那么l2被各条横线所截的线段有怎样的关系?为什么?
探究活动1
一条直线被一组等距的平行线所截得的线段相等.
结论:
l1
l2
准备:数学练习本,利用横格线进行操作
如图,直线a被一组平行线所截,截点分别为A、P、B、Q、R、C,且AP=PB=BQ=QR=RC.
(1)这一组平行线是否等距?
(2)另一条直线b也被这一组平行线所截,截点分别为D、S、E、T、G、F. 填空:
A
P
B
Q
R
C
D
S
E
T
G
F
b
l1
l2
l3
l4
l5
l6
AQ
QC
DT
TF
QC
CA
TF
DF
探究活动1
a
三条距离不相等的平行线截两条直线.
你能否利用所学过的相关知识进行说明?
A
B
C
D
E
F
L1
L2
L3
a
b
探究活动2
Q1
Q2
Q3
m1
m1
m3
结论:
一般地,若l1//l2//l3,且 ,则
(p,q为正整数)
思考:还有其它对应线段成比例吗?
A
B
C
A1
B1
C1
l1
l2
l3
E
F
平行线等分线段定理
反过来,
一条直线被一组平行线所截得的线段相等,
那么在其他直线被这组平行线截得的线段也相等.
几何表述
∵ 直线l1∥l2∥l3 ,AB=BC
∴ A1B1=B1C1
平行线等分线段定理
经过梯形一腰的中点与底平行的直线,必平分另一腰。
?
?
A
B
C
D
E
F
几何表述
∵ 在梯形ABCD中,AD∥EF∥BC,AE=EB
∴ DF=FC
平行线等分线段定理推论
A
E
B
C
F
经过三角形一边的中点与另一边平行的直线,必平分第三边。
几何表述
∵ 在△ABC中,EF∥BC,AE=EB
∴ AF=FC
平行线等分线段定理推论
探究活动
A
B
C
D
E
活动1 将△ABC放置在边长为1的小正方形网格中,平行于边BC的直线l交AB于点D,交AC于点E. 如图,判断△ADE与△ABC是否相似,需要证明哪些条件?
l
A
B
C
D
E
l
思考:如果A点不在格点上,线段的比值是否改变?为什么?
探究活动
A
B
C
D
E
活动1 将△ABC放置在边长为1的小正方形网格中,平行于边BC的直线l交AB于点D,交AC于点E. 如图,判断△ADE与△ABC是否相似,需要证明哪些条件?
l
A
B
C
D
E
l
思考:如果A点不在格点上,线段的比值是否改变?为什么?
平行线分线段成比例
人教版数学九年级下册第二十七章《相似三角形》
特别地,如果两个三角形的三个角分别相等,三条边成比例时,这两个三角形相似.
知识回顾
当两个多边形,满足什么条件时相似?
A
C′
B′
A′
C
B
定义判定法:
三个角分别相等,三条边成比例的两个三角形相似.
除了定义判定法,类比全等三角形的判定,
猜一猜相似三角形的判定方法还有哪些?
A
C′
B′
A′
C
B
= k
∴△ABC △A B C
∵
∽
概念生成
A
E
B
C
F
思考:如图,若点E为AB中点,EF平行于BC,则=____.
情境导入
如图,EF是△ABC的中位线,则图中有哪些成比例的线段?
A
B
C
D
E
F
l1
l2
l3
a
b
探究活动1
如图,已知直线l1//l2//l3,它们分别与直线a,b交于点A,B,C,D,E,F,若AB=BC,则=____.
思考:图中有哪些线段成比例
A
B
C
D
E
F
l1
l2
l3
a
b
探究活动2
如图,已知直线l1//l2//l3,它们分别与直线a,b交于点A,B,C,D,E,F,若= ,则=____.
思考:图中还有哪些线段成比例
结论生成
两条直线被一组平行线所截,所得对应线段成比例.
几何表述
∵ 直线l1∥l2∥l3
∴
A
B
C
D
E
F
l1
l2
l3
a
b
平行线分线段成比例的基本事实
例1 如图,l1∥l2∥l3,且AB=2BC,
(1)求和的值;
(2)若AG=4cm,DF=5cm,
求线段GF,EF的长.
结论应用
课堂练习:完成课本p31第1题
探究活动3
平行线分线段成比例的基本事实与三角形的联系
a
A
D
B
b
E
C
l1
l2
l3
a
D
A
B
b
E
C
l1
l2
l3
思考:平行于△ABC的边BC的直线,分别交直线AB、BC于D、E两点,可以得到哪些相等的线段比?
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
例2 如图,在△ABC中,DE//BC,且AD=3,DB=2,求的值.
结论应用
思考:你能求出的值吗?
类比:在△ABC中,DE//BC,
求证:= = .
F
三对角相等
△AED∽△ACB
“A”型
“8”型
(图2)
D
E
A
B
C
A
B
C
D
E
(图1)
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
结论生成
相似三角形的平行判定定理
几何表述?
例3 如图,在△ABC中,DE//BC,F在BC边上,连接AF交ED于点G,
(1)图中共有几对相似三角形?
(2)写出所有与相等的线段比.
结论应用
F
G
练习2:如图,AD∥EG∥BC,EG分别交AB、DB、AC于点E、F、G,
(1)图中有几对相似三角形,请都写出来;
(2)若AD=6,BC=10,AE=3,AB=5,求EG、FG的长.
结论应用
归纳:求线段的长,找线段所在的三角形,及与之相似的三角形,对应边成比例!
课堂小结
今天你学到了什么?从知识和思想方法两个方面说明.
作业:加油站p19,+p20第9,12,13题
(1)在横格纸上画直线l1,使得l1与横线垂直,观察直线l1被各条横线所截的线段之间有怎样的关系?
(2)再任意画一条直线l2,那么l2被各条横线所截的线段有怎样的关系?为什么?
探究活动1
一条直线被一组等距的平行线所截得的线段相等.
结论:
l1
l2
准备:数学练习本,利用横格线进行操作
如图,直线a被一组平行线所截,截点分别为A、P、B、Q、R、C,且AP=PB=BQ=QR=RC.
(1)这一组平行线是否等距?
(2)另一条直线b也被这一组平行线所截,截点分别为D、S、E、T、G、F. 填空:
A
P
B
Q
R
C
D
S
E
T
G
F
b
l1
l2
l3
l4
l5
l6
AQ
QC
DT
TF
QC
CA
TF
DF
探究活动1
a
三条距离不相等的平行线截两条直线.
你能否利用所学过的相关知识进行说明?
A
B
C
D
E
F
L1
L2
L3
a
b
探究活动2
Q1
Q2
Q3
m1
m1
m3
结论:
一般地,若l1//l2//l3,且 ,则
(p,q为正整数)
思考:还有其它对应线段成比例吗?
A
B
C
A1
B1
C1
l1
l2
l3
E
F
平行线等分线段定理
反过来,
一条直线被一组平行线所截得的线段相等,
那么在其他直线被这组平行线截得的线段也相等.
几何表述
∵ 直线l1∥l2∥l3 ,AB=BC
∴ A1B1=B1C1
平行线等分线段定理
经过梯形一腰的中点与底平行的直线,必平分另一腰。
?
?
A
B
C
D
E
F
几何表述
∵ 在梯形ABCD中,AD∥EF∥BC,AE=EB
∴ DF=FC
平行线等分线段定理推论
A
E
B
C
F
经过三角形一边的中点与另一边平行的直线,必平分第三边。
几何表述
∵ 在△ABC中,EF∥BC,AE=EB
∴ AF=FC
平行线等分线段定理推论
探究活动
A
B
C
D
E
活动1 将△ABC放置在边长为1的小正方形网格中,平行于边BC的直线l交AB于点D,交AC于点E. 如图,判断△ADE与△ABC是否相似,需要证明哪些条件?
l
A
B
C
D
E
l
思考:如果A点不在格点上,线段的比值是否改变?为什么?
探究活动
A
B
C
D
E
活动1 将△ABC放置在边长为1的小正方形网格中,平行于边BC的直线l交AB于点D,交AC于点E. 如图,判断△ADE与△ABC是否相似,需要证明哪些条件?
l
A
B
C
D
E
l
思考:如果A点不在格点上,线段的比值是否改变?为什么?
